主要划分方式及其分类
按密钥方式划分:对称,非对称
按明文处理方式分:块密码,流密码
按编制原理划分:代换,置乱
对称加密算法
对称加密算法 对称加密算法(synmetric algorithm),也称为传统密码算法,其加密密钥与解密密钥相同或很容易相互推算出来,因此也称之为秘密密钥算法或单钥算法。对称算法分为两类,一类称为序列密码算法(stream cipher),另一种称为分组密码算法(block cipher)。 对称加密算法的主要优点是运算速度快,硬件容易实现;其缺点是密钥的分发与管理比较困难,特别是当通信的人数增加时,密钥
发送方和接收方的密钥相同
非对称加密
非对称加密算法也称公开密钥算法;公开密钥体制把信息的加密密钥和解密密钥分离,通信的每一方都拥有一对密钥:公钥、私钥;公开密钥体制最大的优点:不需要对密钥通信进行保密,所需传输的只有公开密钥;这种密钥体制还可以用于数字签名;公开密钥体制的缺陷:加密和解密的运算时间比较长,在一定程度上限制了它的应用范围。
解密和加密的密钥不同,且互相无法推算出来
替换密码(古典密码学)
单表代换密码
多表替换密码
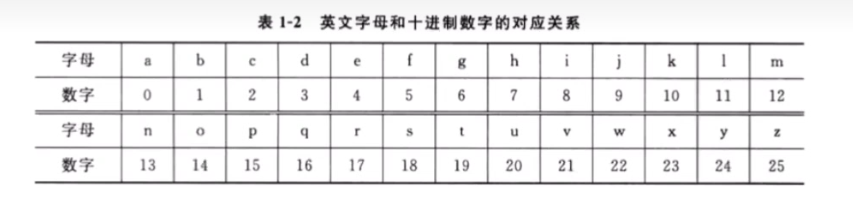
Vigenere密码是一种典型的多表替换密码算法。算法如下:设密钥K=k1k2……kn,明文M=m1m2……mn,加密变换:ci≡(mi+ki)mod 26,i=1,2,……,n解密变换:mi≡(ci-ki)mod 26,i=1,2,……,n例如:明文X=cipher block,密钥为:hit则把明文划分成长度为3的序列:cip her blo ck每个序列中的字母分别与密钥序列中相应字母进行模26运算,得密文:JQI OMK ITH JS
凯撒密码

移位变化(移位密码)
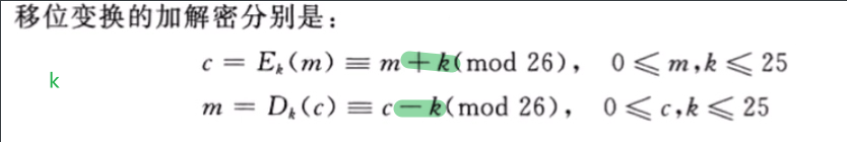
放射变换

解密需要拓展欧几里得…..吃饱了撑的?。
替换密码的特点是:依据一定的规则,明文字母被不同的密文字母所代替。
移位密码移位密码基于数论中的模运算。因为英文有26个字母,故可将移位密码定义如下:令P={A,B,C,……Z},C={A,B,C,……Z},K={0,1,2,……25},加密变换:Ek(x)=(x+k)mod 26解密变换:Dk(y)=(y-k)mod 26
…这给的例子么玩意?(课件上的)
置乱密码
置乱密码的特点是保持
明文的所有字母不变
,只是
利用置换(加入一个算法)*
*打乱明文字母出现的位置
。置乱密码体制定义如下:令m为一正整数,P=C={A,B,C,……Z},对任意的置换π(密钥),定义:加密变换:Eπ(x1,x2,……,xm)=(xπ(1), xπ(2)……, xπ(m)), 解密变换:Dπ(y1,y2,……,ym)=(xπ-1(1), xπ-1 (2)……, xπ-1 (m)),
置乱密码也不能掩盖字母的统计规律**(注意),因而不能抵御基于统计的密码分析方法的攻击。


DES算法
首先把明文分成若干个64-bit的分组,算法以一个分组作为输入;通过一个初始置换(IP);将明文分组分成左半部分(L0)和右半部分(R0),各为32-bit;然后进行16轮完全相同的运算,这些运算我们称为函数f,在运算过程中数据与密钥相结合;16轮运算后,左、右两部分合在一起,经过一个末转换(初始转换的逆置换IP-1),输出一个64-bit的密文分组。
初始置乱
S-BOX
P-BOX
子密钥生成
DES解密
caeasar密码*
看看就行蛤,别人一辈子的东西写在一本书里,可你指望几天就掌握,这样不是人心不足蛇吞象了吗?,浙大翁凯老师在中国mooc上讲c语言说的一句话我一直记得:‘计算机里没有黑魔法,所有的都只是我现在不会’,我说:all is well
void encrypt(char* text,int k,char cipher[1024]){ int a[26];int A[26]; int m; for(int i=97;i<123;i++){ a[i-97]=i; A[i-97]=i-32; }
int len=strlen(text);
for(int j=0;j<len;j++){
int t=text[j];
if(96<t&&t<123){
m=(text[j]+k-97)%26;
cipher[j]=a[m];
}
else if(64<t&&t<91){
m=(text[j]+k-65)%26;
cipher[j]=A[m];
}
else
cipher[j]=' ';
}
}
void decrypt(char* cipher,int k,char text[1024]){ int a[26];int A[26]; int m; for(int i=97;i<123;i++){ a[i-97]=i; A[i-97]=i-32; } int len=strlen(cipher); for(int i=0;i<len;i++){ int t=cipher[i]; if(96<t&&t<123){ m=(cipher[i]-k-71)%26; text[i]=a[m]; } else if(64<t&&t<91){ m=(cipher[i]-k-39)%26; text[i]=A[m]; } else text[i]=' '; }}
单表置换*
//#include "Ceasar.h"#include "stdafx.h"
void transkey(char* key,char table[27]){ char tem[100]={0}; char table1[30]={0}; for(int i=97;i<123;i++) table1[i-97]=i;
int len1=strlen(key);
strcpy(tem,key);
strcpy(tem+len1,table1);
int len=strlen(tem);
int k=1;int flag;
if(isupper(tem[0]))
tem[0]+=32;
table[0]=tem[0];
for(int i=1;i<strlen(tem)&&k<26;i++){
if(!isalpha(tem[i]))
continue;
if(isupper(tem[i]))
tem[i]+=32;
flag=0;
for(int j=0;j<k;j++){
if(table[j]==tem[i]){
flag=1;break;
}
}
if(!flag)
table[k++]=tem[i];
}
}void encrypt(char* text,char* key,char cipher[1024]){ char table[27]={0}; transkey(key,table);
int len=strlen(text);
for(int i=0;i<len;i++){
if(!isalpha(text[i]))
cipher[i]=text[i];
else if(islower(text[i]))
cipher[i]=table[text[i]-97];
else
cipher[i]=table[text[i]-65]-32;
}
}
void ttable(char table[27]){ char ip[30]={0}; for(int i=97;i<122;i++){ ip[table[i-97]-'a']=i; } memcpy(table,ip,26);
}void decrypt(char* cipher,char* key,char text[1024]){ char table[27]={0}; transkey(key,table); ttable(table);
int len=strlen(cipher);
for(int i=0;i<len;i++){
if(!isalpha(cipher[i]))
text[i]=cipher[i];
else if(islower(cipher[i]))
text[i]=table[cipher[i]-97];
else
text[i]=table[cipher[i]-65]-32;
}
}
仿射变换*
//#include "Ceasar.h"#include "stdafx.h"
void encrypt(char* text,int k1,int k2,char cipher[1024]){ int len=strlen(text); int e=0; for(int j=0;j<len;j++){ if(!isalpha(text[j])){ cipher[j]=text[j]; } else if(islower(text[j])){ e=text[j]-'a'; cipher[j] = (ek1+k2) % 26 + 'a'; } else{ e=text[j]-'A'; cipher[j] = (ek1+k2) % 26 + 'A'; } }
}
int rec(int k,int m){ int i=1; int j=0; while(1){ for(j=0;kj<mi+1;j++){} if(kj==mi+1) break; else i++; } return j;}void decrypt(char* cipher,int k1,int k2,char text[1024]){ int len=strlen(cipher); int e=0; int k3=rec(k1,26); for(int i=0;i<len;i++){ if(!isalpha(cipher[i])){ text[i]=cipher[i]; } else if(islower(cipher[i])){ e=cipher[i]-'a'; text[i] = (k3(e-k2+26))% 26 + 'a'; } else{ e = cipher[i] - 'A'; text[i]=((e-k2+26)k3)% 26 +'A'; } }
}
维吉尼亚密码*······················································
//#include "Ceasar.h"#include "stdafx.h"
void encrypt(char* text,char* key,char cipher[1024]){ int len=strlen(text); int lenkey=strlen(key); for(int j=0;j<lenkey;j++) //keyСд if(isupper(key[j])) key[j]+=32; for(int i=0;i<len;i++){ if(!isalpha(text[i])) cipher[i]=text[i]; else if(isupper(text[i])) cipher[i]=(text[i]-'A'+key[i%lenkey]-'a')%26+'A'; else cipher[i]=(text[i]-'a'+key[i%lenkey]-'a')%26+'a'; }}
void decrypt(char* cipher,char* key,char text[1024]){ int len=strlen(cipher); int lenkey=strlen(key); for(int j=0;j<lenkey;j++) //keyСд if(isupper(key[j])) key[j]+=32; for(int i=0;i<len;i++){ if(!isalpha(cipher[i])) text[i]=cipher[i]; else if(isupper(cipher[i])) text[i]=(26+cipher[i]-'A'-(key[i%lenkey]-'a'))%26+'A'; else text[i]=(26+cipher[i]-'a'-(key[i%lenkey]-'a'))%26+'a'; }}
置乱算法
###
一、算法流程:
需要随机置乱的n个元素的数组a:for i 从n-1到1
j <—随机整数(0 =< j <= i)
交换a[i]和a[j]
end
二、实例实现
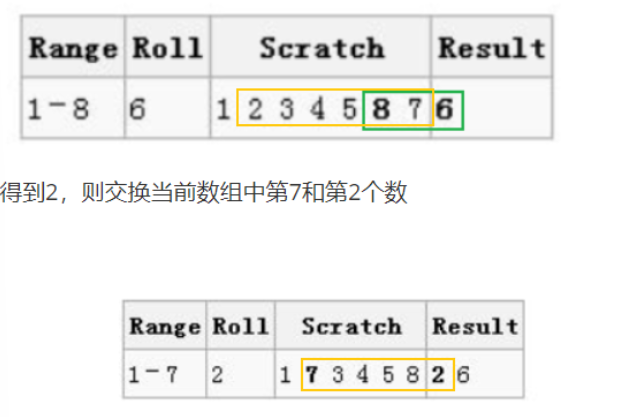
各列含义:范围、当前数组随机交换的位置、剩余没有被选择的数、已经随机排列的数
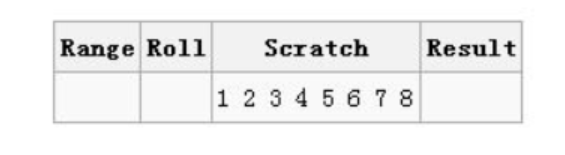
第一轮:从1到8中随机选择一个数,得到6,则交换当前数组中第8和第6个数

第一轮结果
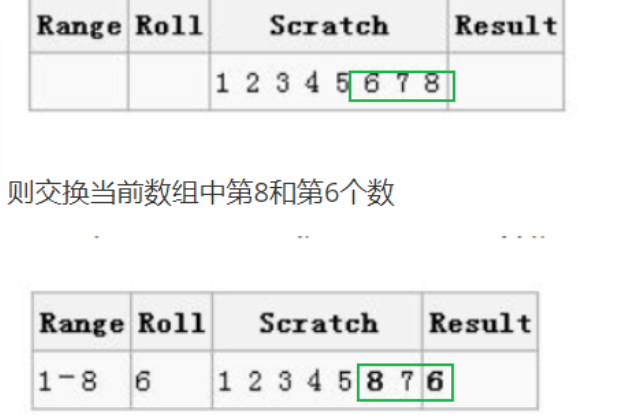
第二论:从1到7中随机选择一个数,得到2,则交换当前数组中第7和第2个数

第二轮结果
总结;
下一个随机数从1到6中摇出,刚好是6,这意味着只需把当前线性表中的第6个数留在原位置,接着进行下一步;以此类推,直到整个排列完成。
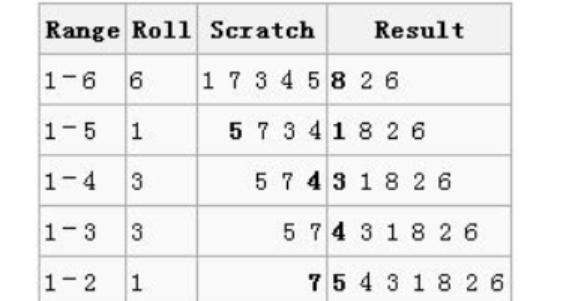
截至目前,所有需要的置乱已经完成,所以最终的结果是:7 5 4 3 1 8 2 6
三、Java源代码
package simpleGa;
import java.util.Arrays;import java.util.Random;
public class Test {
public static void main(String[] args) {
int[] arr = new int[10];
int i;
//初始的有序数组
System.out.println(“初始有序数组:”);
for (i = 0; i < 10; i++) {
arr[i] = i + 1;
System.out.print(” ” + arr[i]);
}
//费雪耶兹置乱算法
System.out.println(“\n” + “每次生成的随机交换位置:”);
for (i = arr.length – 1; i > 0; i–) {
//随机数生成器,范围[0, i]
int rand = (new Random()).nextInt(i+1);
System.out.print(” ” + rand);
int temp = arr[i];
arr[i] = arr[rand];
arr[rand] = temp;
}
//置换之后的数组
System.out.println(“\n” + “置换后的数组:”);
for (int k: arr)
System.out.print(” ” + k);
}
}
分析

从运行结果可以看到随着算法的进行,可供选择的随机数范围在减小,与此同时此时数组里的元素更加趋于无序。
…自己运行呗
关于java中的函数

四、潜在的偏差
在实现Fisher-Yates费雪耶兹随机置乱算法时,可能会出现偏差,尽管这种偏差是非常不明显的。原因:一是实现算法本身出现问题;二是算法基于的
随机数生成器
。
1.实现上每一种排列非等概率的出现
在算法流程里 j 的选择范围是从0…i-1;这样Fisher-Yates算法就变成了Sattolo算法,共有(n-1)!种不同的排列,而非n!种排列。
j在所有0…n的范围内选择,则一些序列必须通过n^n种排列才可能生成。
2.Fisher-Yates费雪耶兹算法使用的随机数生成器是PRNG伪随机数生成器
这样的一个伪随机数生成器生成的序列,完全由序列开始的内部状态所确定,由这样的一个伪随机生成器驱动的算法生成的不同置乱不可能多于生成器的不同状态数,甚至当可能的状态数超过了排列,不正常的从状态数到排列的映射会使一些排列出现的频率超过其他的。所以状态数需要比排列数高几个量级。
很多语言或者库函数内建的伪随机数生成器只有32位的内部状态,意味着可以生成2^32种不同的序列数。如果这样一个随机器用于置乱一副52张的扑克牌,只能产生52! = 2^225.6种可能的排列中的一小部分。对于少于226位的内部状态的随机数生成器不可能产生52张卡片的所有的排列。
伪随机数生成器的内部状态数和基于此生成器的每种排列都可以生成的最大线性表长度之间的关系:
总结学习
也就是经典的雪耶兹(Fisher–Yates) 也被称作高纳德( Knuth)随机置乱算法

雪耶兹(Fisher–Yates) 也被称作高纳德( Knuth)随机置乱算法优缺点进阶分析:
https://blog.csdn.net/weixin_44385465/article/details/110131608?ops_request_misc=&request_id=&biz_id=102&utm_term=%E8%B4%B9%E9%9B%AA%E8%80%B6%E5%85%B9%E9%9A%8F%E6%9C%BA%E7%BD%AE%E4%B9%B1%E7%AE%97%E6%B3%95%E7%9A%84%E4%B8%8D%E8%B6%B3&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-2-110131608.142
^v47^control,201^v3^control_1&spm=1018.2226.3001.4187