一、离散傅立叶变换

1.fft/ ifft——快速傅立叶变换/反变换

• Y=fft(X)/Y=ifft(X)函数
  
  按照基2的算法对X进行快速傅立叶变换/反变换。若X是一个矩阵，则对矩阵的每列进行快速傅立叶变换l反变换，返回Y是和X相同大小的矩阵。若X是一个多维序列，则对第一个非单独维进行快速傅立叶变换/反变换。
• Y=fft(X,n)/Y=ifft(×,n)函数
  
  对X进行n点快速傅立叶变换/反变换。当X是一个向量，若X的长度小于n，则先对X进行补零使其长度为n;若X的长度大于n，则对X进行剪切使其长度为n，最后得到一个长度为n的向量Y。当X是一个矩阵，则利用同样方法对矩阵的每一列进行调整，然后对矩阵的每列进行快速傅立叶变换/反变换，最后得到一个n行的矩阵Y。
• Y=fft(X,n,dim)/Y=ifft(×,n,dim)
  
  用法同上。dim用来指定进行快速离散傅立叶变换/反变换的维数。

2.fftn-进行n维快速傅里叶变换

• Y = fftn(X)运用多维快速傅里叶变换（FFT)算法，计算X的n维离散傅里叶变换值。参量X可为向量、矩阵和多维数组。
• Y = fftn(X,size)运用多维快速傅里叶变换(FFT）算法，计算X的n维离散傅里叶变换值。参量size为向量，其元素指定变换前X各维的大小。如果X的维数与size不同，则对X进行补零或截短后进行计算。

代码示例：

y = fftn(rand(50));
t = fftn(rand(50),[100 100]);

运行结果：

3.fft2-进行2维快速傅里叶变换

• Y =fft2(X)计算矩阵X的二维离散傅里叶变换矩阵Y。X和Y的维数相同。
• Y = fft2(×,m,n)计算矩阵X的二维离散傅里叶变换矩阵Y。在变换前先将X补零至m×n矩阵。如果m或n比A的维数小，则将X截短。Y的维数为m×n。

代码示例：

y = fft2(rand(10));
t = fft2(rand(50),20,20);

运行结果：

代码示例：

I=imread('rabbit.jpg');
I = rgb2gray(I);      
subplot(121);imshow(I)
% 求离散傅立叶频谱
J=fftshift(fft2(I));
subplot(122);imshow(log(abs(J)),[8,10])

二、离散余弦变换

1.dct2 函数

功能：

二维离散余弦变换全页折叠


语法：

• B = dct2(A)
  
  返回 A 的二维离散余弦变换。矩阵 B 包含离散余弦变换系数 B(k1,k2)。
• B = dct2(A,m,n) or B = dct2(A,[m n])
  
  B = dct2(A,m,n) 和B = dct2(A,[m n]) 用 0 对矩阵 A 进行填充，使其大小为 m×n。如果 m 或 n 小于 A 的对应维度，则 dct2 在变换前对 A 进行裁切。

代码示例：

I=imread('rabbit.jpg');
I = rgb2gray(I);      
subplot(121);imshow(I);
J = dct2(I);
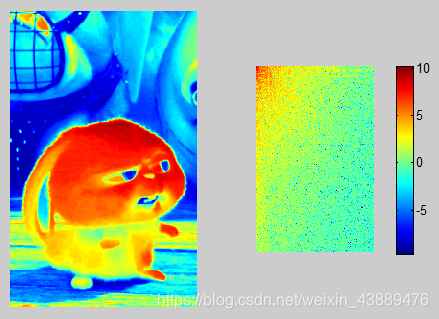
subplot(122);imshow(log(abs(J)),[])
colormap(jet)
colorbar
J(abs(J)<10) = 0;
K = idct2(J);
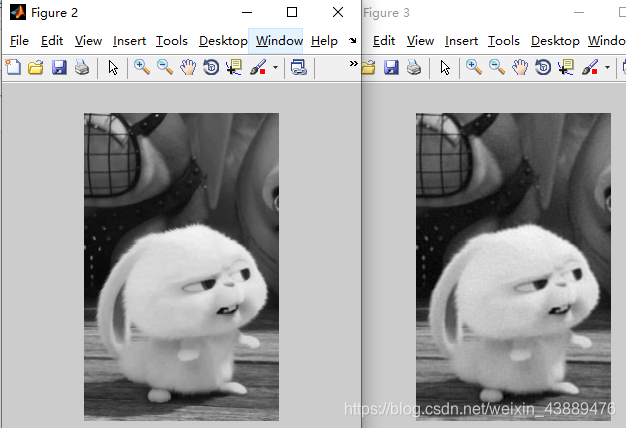
figure, imshow(I)
figure, imshow(K,[0 255])
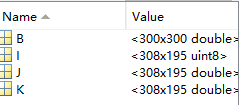
B = dct2(I,300,300);

运行结果：

2.dict2 函数

功能：

DCT 反变换


格式：

• B=idct2(A)
• B=idct2(A,m,n)
• B=idct2(A,[m,n])
  
  
  说明：
  
  
  B＝idct2(A) 计算 A 的 DCT 反变换 B ，A 与 B 的大小相同；
  
  B＝idct2(A,m,n) 和 B=idct2(A,[m,n]) 通过对 A 补 0 或剪裁，使 B 的大小为 m×n。

3.dctmtx 函数

功能：

计算 DCT 变换矩阵


格式：

D＝dctmtx(n)


说明：


D＝dctmtx(n) 返回一个 n×n 的 DCT 变换矩阵，输出矩阵 D 为 double 类型


代码示例：

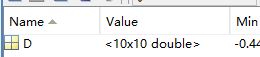
D=dctmtx(10)

运行结果：