完全二叉树简析
摘要:解释了数据结构树中的重要形态之完全二叉树
。
在数据结构的学习中,我们会学到重要的一章:树,树是一种逻辑结构,我们使用连续存储可非连续存储都能实现树,同时,就像顺序表和链表中都能实现栈和队列一样,不管是什么存储方式存储的树,都有操作受限的子逻辑结构,树也不例外,树存在:完全二叉树,二叉排序树,大小顶堆,B-树,红黑树等特殊的树,这些树通常都是迎合某些特殊的场合而设计的,不存在哪个好哪个不好的概念。这篇文章主要是简要讲解什么是完全二叉树。
完全二叉树的定义
完全二叉树的官方定义为:
一棵深度为k的有n个结点的
二叉树
,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与
满二叉树
中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。(引用自百度百科)
我们可以更为简单的理解为:对于一些节点,我们按照二叉树的排列规则,从左到右的依次向下排列,中间不能有空位,就叫完全二叉树,如图所示,我们有一些节点,我们将这些节点遵循二叉树的结构,一层一层的致密的从左到右进行插入分配:
如图我们得到了一些节点,接下来我们从中取不断取节点,并按照二叉树的原则,在树的每一层上,都从左到右的排布满:
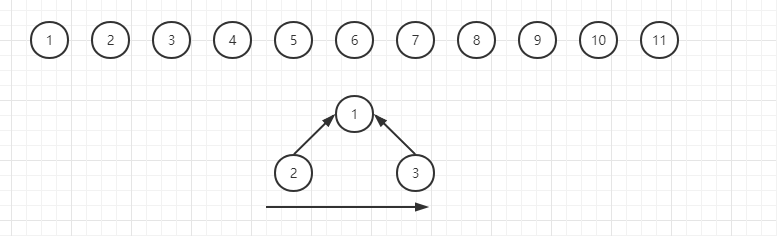
如图上图所示,我们在第二层从左到右的排满了这一层。
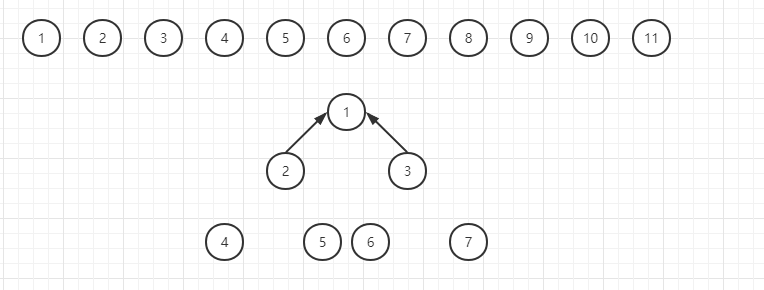
如上图所示,低三层若是想要排布满,我们根据二叉树规则知道,我们需要四个节点,因此我们从左到右的放入四个节点,然后连线成树:
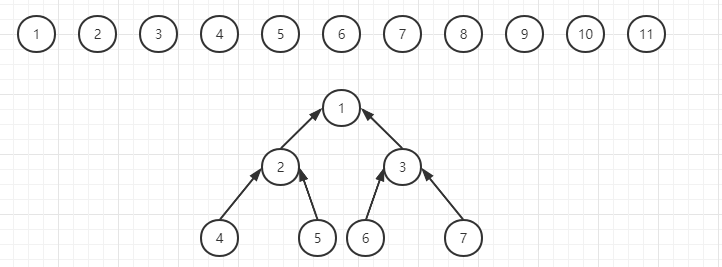
接下来我们继续排布,我们根据二叉树的规则知道下一层需要8个节点,但是从图中可知节点不够了,但是我们仍然要依照从左到右的次序依次排布:
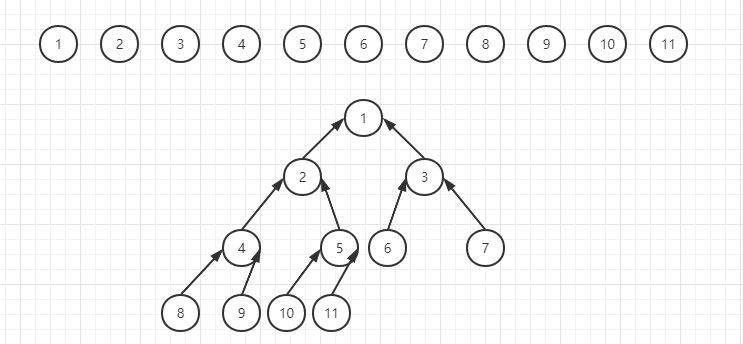
在我们完全插入完成之后,便会得到一棵这样的数,我们可以发现,这棵树的节点,每一层都是从左向右依次排布的,最后一个节点为11,它位于整棵树的最右下角,只有它后边有空位,它之前是没有空位的,这样的树就叫完全二叉树。
现在我们可以理解,
完全二叉树就是一棵只能在最后一层的最右一个不为空的位置上进行增删操作的树
,在创建一棵完全二叉树时,我们进行的所有添加行为,都只能是在这个位置上插入,而在删除操作时,也只能在这个位置上删除,正因为这种受限制的插入删除,导致了完全二叉树是这种样子的,也就是这棵树位于最右下角的节点之前没有任何一个空位置。
完全二叉树的应用
完全二叉树的好处在于使用完全二叉树,我们可以直击在不修改数组形态的状态下,直接将一个数组映射成一棵树,然后通过这棵树对数组操作,同时很多其他结构的树也都要求这棵树是完全二叉树,如堆就要求堆是一棵完全二叉树。