神经网络算法起源于人们对大脑的研究,是模拟大脑学习功能的算法。
脑科学中有一个假说——
one learning algorithm
。就是说大脑中负责躯体感觉的脑细胞,如果你将它连接到眼睛上,或者用视觉传感器给它传递视觉信号,它会学会看,会产生视觉。这就给了我们一个启示——既然脑细胞可以通过学习学会它本不会的功能,那我们也可以模拟脑组织设计出一个系统,学习各种功能。这样就产生了人工神经网络。

大脑复杂的功能是由数以亿计的神经元构成的复杂神经网络完成的,如下图所示,神经元的树突接受电信号(dendrite),细胞体(Nucleus)进行处理,轴突(Axons)输出电信号。无数神经元连接在一起构成神经网络,通过电信号传递信息,进而完成各种功能。

接下来就介绍神经网络算法的结构与工作原理:
人工神经网络结构的基本单元是一个个逻辑回归单元。如下图所示,看得出这个结构很像神经元,x1、x2和+1是输入,橘色的圆圈代表激活函数(activation function),也就是神经元的细胞体,对输入进行处理,然后输出
![]()
。

激活函数仍为sigmoid函数,可以认为z>4.6时输入近似为1,z<-4.6时输出近似为0。

许多逻辑回归单元构成神经网络,如下图所示。
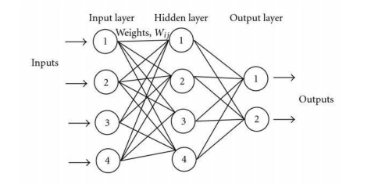
数据进入输入层,在隐藏层进行处理,从输出层输出。每一层之间的每一条连线对应一个权重θ,整个网络的权重值构成权重矩阵Θ,例如上面的神经网络为2
×
4权重矩阵,
![]()
表示第一层的权重值构成的向量,
![]()
表示从第一层第一个神经元的输出到第二层第二个神经元输入时所赋予的权重,注意上标表示层数;
![]()
表示第一层第二个神经元的输入,因此
![]()
可表示为如下:
![]()
![]()
![]()
表示第一层第二个神经元的输出,是该神经元加权输入
![]()
的函数:
![]()
=
![]()
当我们将数据输入到input layer,数据经过
前向传输
到达输出层,过程如下。
![]()
就是网络对输入数据
![]()
的输出,可通过调整输入的数据
![]()
和各个权重值θ让输出接近于标签值。
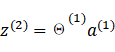
![]()
Add
![]()
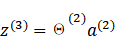
![]()
一个非常好的过程图如下,可以很好地帮助理解前向传输过程。



通过设计复杂的神经网络我们可以拟合非线性函数,例如异或。输入相同时输出0,不同时输出1,如下图所示,显然我们无法用线性函数拟合它。


因此我们可以选择一个合适的神经网络,调整参数如下,此时:
![]()
,
![]()
,
![]()
。
可得真值表如下,实现了异或逻辑。


另外,利用神经网络我们可以实现
多元分类
(one-vs-all),例如我们要将输出分为四个类别,神经网络结构如下所示,此时输出可用四维向量表示如下。若输入一些特征,网络识别它为第二类,那么向量第二个元素为1其余3个为0,表示第二类。


下一篇将介绍反向传播算法,这是神经网络中较难的一部分,因此专门留一章介绍。