信号的时域处理
一、要求
选择子作业1中的音频信号,自行给定滤波器的系统函数,分别采用
时域线性卷积
和
差分方程
两种方法对音频信号进行滤波处理,比较滤波前后信号的波形和回放的效果。
二、实现思路
1.时域卷积法
-
分析原始音频信号的频谱,观察有用信号和噪声的分布,选择滤波器类型(低通、高通、带通、带阻等)
-
设定幅频响应下降三分贝的截止频率和滤波器阶数
-
选择合适的窗函数(包括Rectangular、Hanning、Hamming、Bartlett、Blackman、Kaiser、Gaussian、Flat-top等)
-
计算滤波器系数(滤波器的单位脉冲响应)
-
将滤波器系数与原始信号卷积进行滤波
2.差分方程法
- 分析原始音频信号的频谱,观察有用信号和噪声的分布,选择滤波器类型(低通、高通、带通、带阻等)
- 设置通带截止频率和阻带截止频率并归一化,设定通带纹波系数和阻带衰减系数
- 求出切比雪夫滤波器的阶数和下降3分贝通带截止频率
- 计算滤波器的差分方程系数
- 调用filter函数对原始信号进行滤波
三、实现过程
滤波前后对比图
|
FIR hamming窗低通滤波器前后对比图 |
IIR 切比雪夫低通滤波器前后对比图 |
1.时域卷积
首先导入原始音频信号并画出时域图和幅频响应曲线,分析其频谱分布,代码如下所示。
%% 数据导入及参数设置
[x,Fs]=audioread('D:\数据\Carmen_overture_noisy_8k_9.5k.wav');
Nx=length(x);
tx=(0:Nx-1)/Fs;%时域范围
df=Fs/length(tx); %计算谱线间隔
fx=tx*df;%频域范围
X=FFT(x,Nx,Fs,tx);%快速傅里叶变换
fx=(fx*Fs)/1e3;%只显示正频谱
X=abs(X);
% 绘出时域图和幅频响应
figure;
subplot(221)
plot(tx,x);
title("原信号音频时域图");
xlabel("t/s");
subplot(222)
% plot(fx*Fs/1e3,abs(X),"blue")
plot(fx(1,1:ceil(Nx/2)),X(1:ceil(Nx/2),1),'b')
title("原信号音频相频响应");
xlabel("f/Khz");

观察其幅频响应发现有用信号的频率在8Khz以下,以上则为能量较大的高频噪声,因此我采用低通滤波器对其进行滤波。
FIR滤波器
设FIR滤波器的单位冲激响应h(n)为一个N点序列,0≤n≤N-1,则滤波器的系统函数为:
H
(
z
)
=
∑
k
=
0
N
−
1
h
(
k
)
∗
z
−
k
H(\mathrm{z})=\sum_{k=0}^{N-1}h(\mathrm{k})*\mathrm{z}^{-k}
H
(
z
)
=
k
=
0
∑
N
−
1
h
(
k
)
∗
z
−
k
直接型FIR滤波器
的差分方程为:
y
(
n
)
=
∑
m
=
0
N
−
1
h
(
m
)
x
(
n
−
m
)
\mathrm{y(n)}=\sum_{m=0}^{N-1}\mathrm{h(m)x(n-m)}
y
(
n
)
=
m
=
0
∑
N
−
1
h
(
m
)
x
(
n
−
m
)
由差分方程可知只需要求出FIR滤波器的单位冲激响应h(n),设置
滤波阶数
和
3db通带截止频率fc
,采用
汉林窗函数
处理,再使用
fir1函数
将其与待滤波信号卷积即可完成滤波,具体实现代码如下。
%% hamming窗低通滤波器滤除高频噪声
fc=7.95e3; %下降3分贝截止频率
h_n=fir1(1000,fc*2/Fs,"low");
y=conv(h_n,x);
Ny=length(y);%滤波后信号的长度
ty=(0:Ny-1)/Fs;%时域范围
Y=FFT(y,Ny,Fs,ty);%快速傅里叶变换求频谱
df=Fs/length(ty); %计算谱线间隔
fy=ty*df;%频域范围
fy=(fy*Fs)/1e3;%只显示正频谱
Y=abs(Y);
% 绘出滤波后的时域图和幅频响应
subplot(223)
plot(ty,y,"g");
title("滤波后信号音频时域图");
xlabel("t/s");
subplot(224)
stem(fx(1,1:ceil(Ny/2)),Y(1:ceil(Ny/2),1),'c','.')
title("滤波后信号音频相频响应");
xlabel("f/Khz");
%% 试听及保存
% sound(y,Fs);
audiowrite("D:\数据\FIRfilter.wav",y,Fs);
%% 快速傅里叶变换函数
function FourierTransform = FFT(signal,N,fs,t)
Y=fft(signal,N);
df=fs/length(t); %计算谱线间隔
f=t*df;%频域范围
Ys=abs(Y); %幅度响应
FourierTransform=Ys;
end
FIR滤波器的单位冲激响应如下图所示:
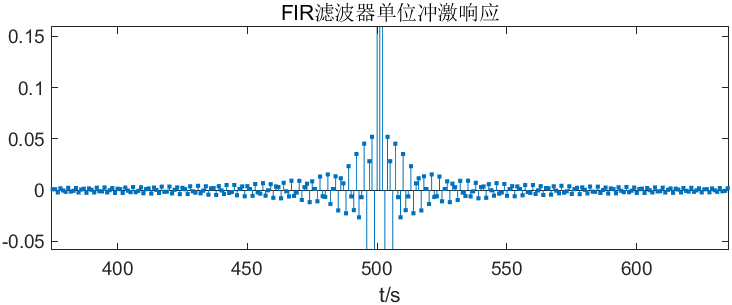
通过时域卷积得到滤波后的结果如下图所示:
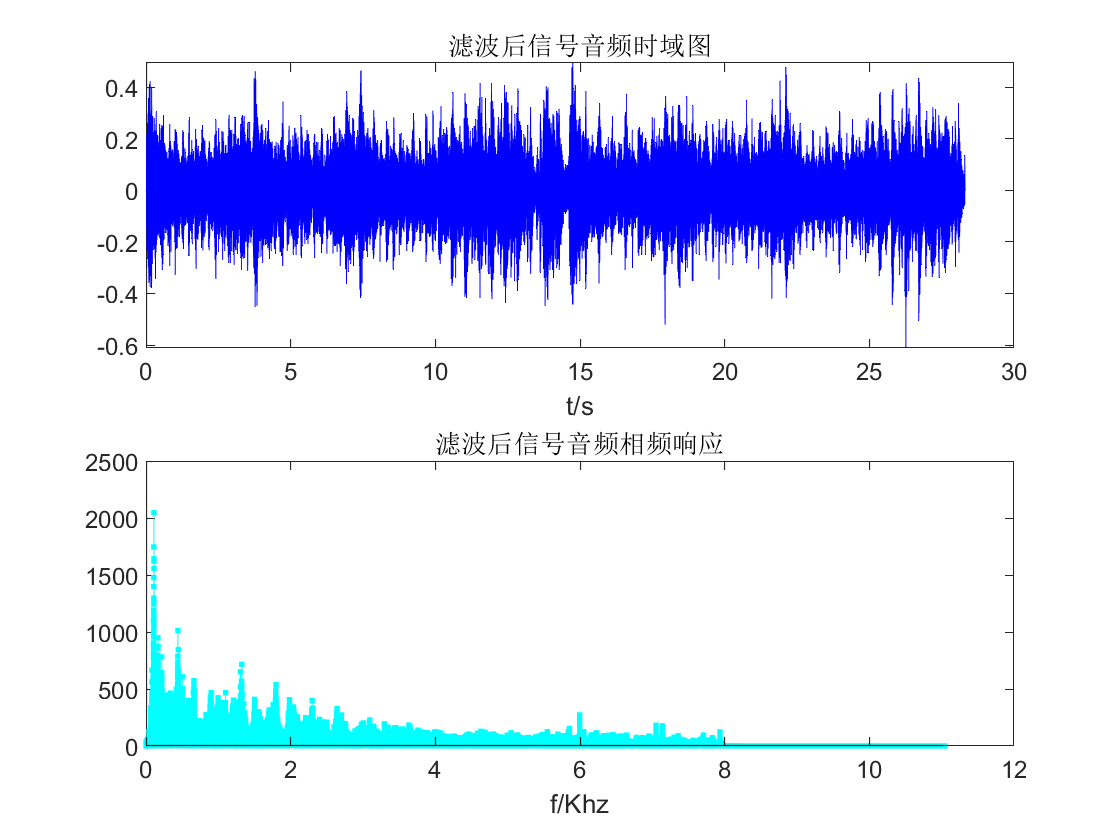
由图可知,发现经过
1000阶
的3分贝截止频率为
7.95e3Khz
的低通滤波器处理后,8Khz及以上的高频噪声基本被完全滤除,成功从原始音频信号中提取到有用信号。
2.差分方程
首先也是先对原始音频信号做傅里叶变换分析其频谱,频谱结果同上,这里不在赘述。
IIR切比雪夫低通滤波
IIR(infinite impulse response)滤波器,无限冲激响应滤波器,IIR滤波器定义如下:
∑
l
=
0
N
a
(
l
)
y
(
n
−
l
)
=
∑
k
=
0
M
b
(
k
)
x
(
n
−
k
)
\sum_{l=0}^{N}a(l)y(n-l)= \sum _{k=0}^{M}b(k)x(n-k)
l
=
0
∑
N
a
(
l
)
y
(
n
−
l
)
=
k
=
0
∑
M
b
(
k
)
x
(
n
−
k
)
令
a
(
0
)
=
1
,
a
(
l
)
,
l
=
1
,
2
,
.
.
.
N
a(0)=1,a(l),l=1,2,…N
a
(
0
)
=
1
,
a
(
l
)
,
l
=
1
,
2
,
…
N
取反后得:
y
(
n
)
=
∑
k
=
0
M
b
(
k
)
x
(
n
−
k
)
+
∑
l
=
1
N
a
(
l
)
y
(
n
−
l
)
y(n)= \sum _{k=0}^{M}b(k)x(n-k)+ \sum _{l=1}^{N}a(l)y(n-l)
y
(
n
)
=
k
=
0
∑
M
b
(
k
)
x
(
n
−
k
)
+
l
=
1
∑
N
a
(
l
)
y
(
n
−
l
)
IIR直接II型滤波器
的流程框图如下所示:

根据流程框图可知,需要求得
差分方程系数向量a和b
,这里我采用常见的切比雪夫滤波器设定
通带频率、阻带频率
以及
纹波系数
和
衰减系数
计算出系数a和b,再利用
filter函数
传入系数a、b和待滤波信号即可完成滤波,采用如下代码实现差分方程法实现IIR切比雪夫低通滤波器。
%% IIR-Chebyshev低通滤波器滤除高频噪声
Wp=7.6e3*2/Fs;%通带频率
Ws=8e3*2/Fs;%阻带频率
[n,Wc]=cheb1ord(Wp,Ws,2,40);%计算阶数和3db通带截止频率
[b,a]=cheby1(n,3,Wc);%切比雪夫滤波器返回差分方程系数
freqz(b,a);%绘出滤波器频谱图(幅频响应和相频响应)
y=filter(b,a,x);%滤除高频噪声
Y=FFT(y,N,Fs,t);
Y=fftshift(Y);
Y=abs(Y);
% 绘出滤波后的时域图和幅频响应
subplot(223)
plot(t,y,'b');
title("滤波后信号音频时域图");
xlabel("t/s");
subplot(224)
% plot(f*Fs/1e3,Y,'k');
plot(f(1,ceil(N/2):end),Y(ceil(N/2):end,1),'g')
title("滤波后信号音频幅频响应");
xlabel("f/Khz");
IIR切比雪夫滤波器的归一化频谱图如下所示:
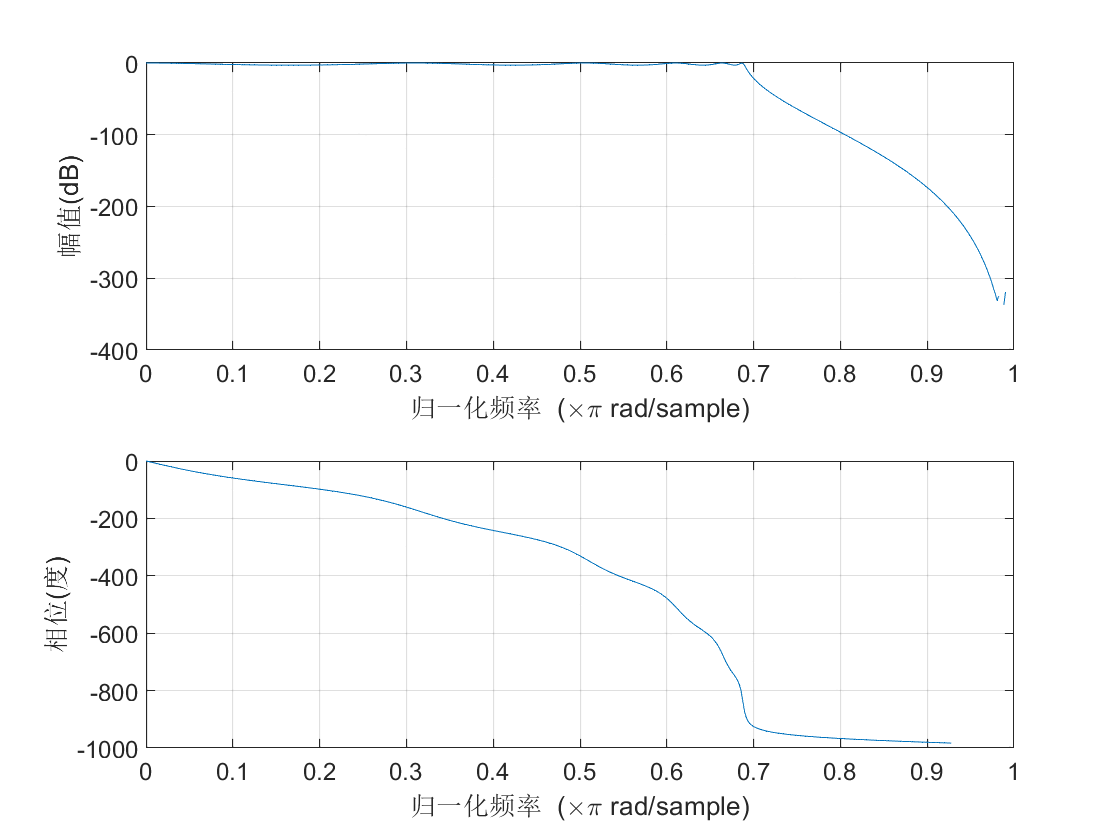
观察发现其幅频响应滤波效果比较好,根据此滤波器对原始音频信号进行滤波,下图展示了滤波后的结果。
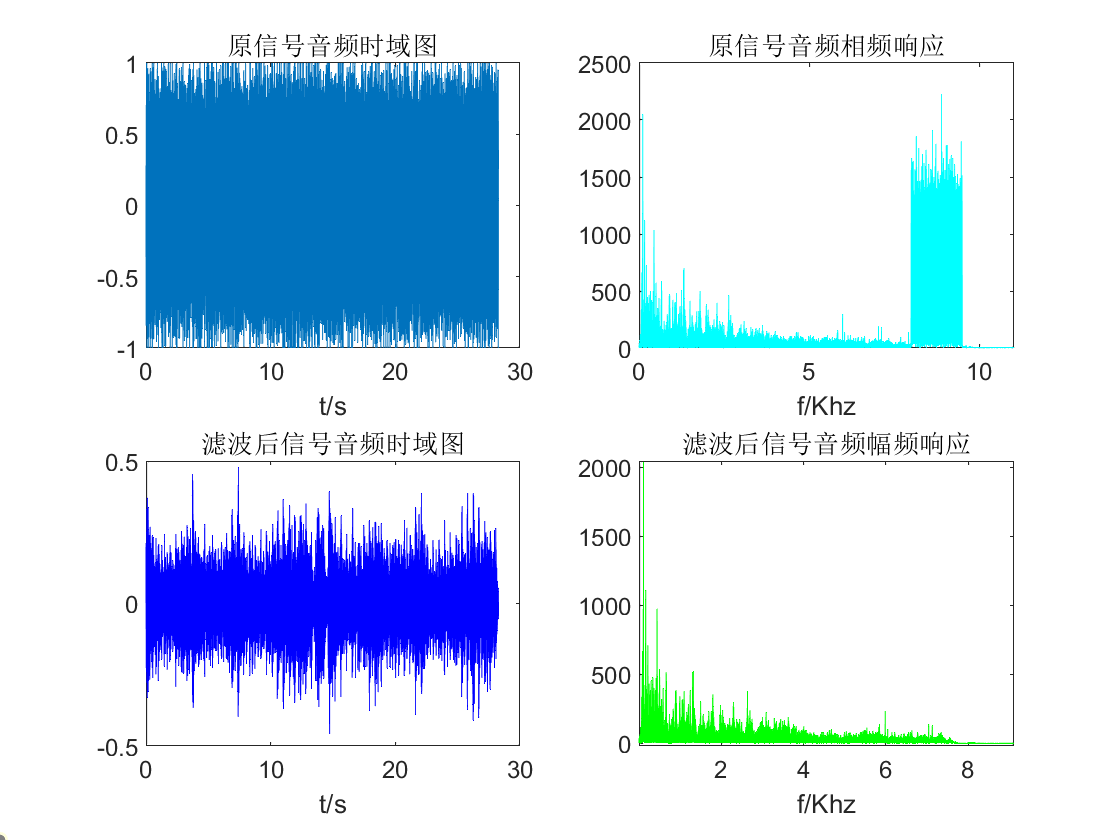
由图可知8Khz及以上的高频噪声被滤除,但原始信号靠近8Khz的部分幅值也有所衰减但影响不大,从而实现了对有用信号的提取。
四、结果分析
-
时域线性卷积法和差分方程法都是实现数字滤波的两种方法,都可以很好的滤除有用信号的噪声,从而提取出有用的信号,排除无用信号的干扰。
-
实际观察发现
随着滤波器的阶数的升高,滤波器的频率响应越接近理想滤波
器,而要想实现同样滤波效果,差分方程法的滤波器阶数远小于时域卷积法的阶数。 -
当使用IIR滤波器时,由于IIR滤波器的存在
系统稳定性
问题,因此当滤波器阶数过高时会导致系统不稳定,从而失去正常滤波能力。 -
将IIR巴特沃斯滤波与切比雪夫滤波器对比,发现
切比雪夫滤波器的滤波效果更好
,频谱对比图如下。
|
切比雪夫滤波后的信号频谱图 |
巴特沃斯滤波后的信号频谱图 |
