注明：本文根据数学建模BOOM网课简单整理，自用
•
指数传播模型与SI模型
❑从最简单的指数传播模型说起
❑ 传染病预测问题
• 不同类型传染病的发病机理和传播途径各有特点
• 有的传染病，在得过一次后可获得
免疫力
，但有的则不会
• 有的传染病具有
潜伏期
，有的则没有
• 需要对不同类型的传染病建立相应合适的预测模型
❑ 从最简单的看起：
指数传播模型
1. 假设所研究的区域是
封闭区域
，在一定时期内人口总量不变，不考虑迁入和迁出
2. 在𝑡时刻患病人数
𝑁(𝑡)
是随时间连续变化的、可微的函数
3. 每个病人在单位时间内会传染到的人数为大于0的
常数
𝜆
❑ 本期课程重点：模型假设与模型改进的思想
❑指数传播模型
❑ 模型的建立
• 设𝑁(𝑡)为𝑡时刻患病人数，则𝑡 + Δ𝑡时刻的患病人数为𝑁(𝑡 + Δ𝑡)
• 则从𝑡 → 𝑡 + Δ𝑡时间内，净增的患病人数为𝑁 (t + Δ𝑡) − 𝑁(𝑡)
• 根据假设3（每个病人在
单位时间内
会传染到的人数为大于0的
常数𝜆
），有：
• 注意，𝜆在模型中始终是常数（每个病人在
单位时间内
会传染到的人数）
❑ 微分方程
• 基于上一页的第2条模型假设，在上面公式等号两边同时除以Δ𝑡，并令Δ𝑡 → 0
• 可得微分方程：
• 可求得该模型的解析解：
❑ 结果分析
• 模型结果显示，患病人数是
指数型增长
的
• 该模型一般适用于
传染病暴发初期
• 因为在初期，传染源和传染途径往往未知，难以防范
• 但是按照该模型，
𝑡 → ∞
时𝑁（t）→ ∞，这显然是不符合实际的
❑ 模型改进
• 封闭区域内人数有限，
当患病人数越来越多时，健康人群的数量也就越来越少
• 那么单位时间内新增的人数（ 𝑁（t）的导数）也会减少，毕竟没多少人可以被感染了
• 基于以上分析，对模型进行改进，建立
SI模型
❑SI模型
❑ 模型假设
1. 人口总数
：
所研究的区域内人口总数为常数𝑁，既不考虑生死，也不考虑迁移
2. 两类人群
：
人群分为易感染者（
s
usceptible）和已感染者（
i
nfective），设𝑡时刻两类人群在总人口中所占的
比例
分别为s（t）和i（t） ，显然𝑠 (t) + 𝑖 (t) = 1
3. 日感染率
：
每个病人在单位时间（每天）内
接触
的平均人数为
常数𝜆
， 称为
日感染率
；当
病人所接触的是健康者时，会将其感染成病人
4. 不考虑治愈
：
每个病人得病后在传染期内无法治愈，且不会死亡
❑ 注意事项
• 现实中，地区人数并不会真的为常数，总有出生率、死亡率、迁入和迁出等
• 但如果把这些因素考虑进模型，模型会非常复杂；而本题重心是传染病
• 再次强调
模型假设的目的：简化问题
❑ 模型建立
•
细节
：第3条假设中
𝜆
是1个病人单位时间接触的平均人数，
接触的人中
既有病人也有健康者
• 则1个病人单位时间内可使𝜆𝑠(𝑡)个健康者变为病人
• 在𝑡时刻
病人总数
𝑁𝑖(𝑡)（N是常数为该地区总人口），
𝛥𝑡时间
内会
新增
𝜆𝑠(𝑡)𝑁𝑖(𝑡)𝛥𝑡个病人，则
单位时间
内
新增
病人数：
• 令𝛥𝑡 → 0，得微分方程
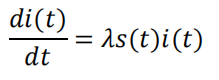
• 根据
第2条假设
， 由于s(t)+i(t)= 1，所以可写作
• 设𝑡 = 0时，患病人数占总人口的比例为i(0) = 𝑖0 ，则SI模型：
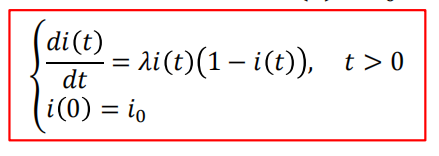
• 求解该微分方程，得
• 该模型其实就是
Logistic模型
，𝑖(t)是病人占总人口的比例，最大值为1，即当t→∞时，区域内所有人都被传染
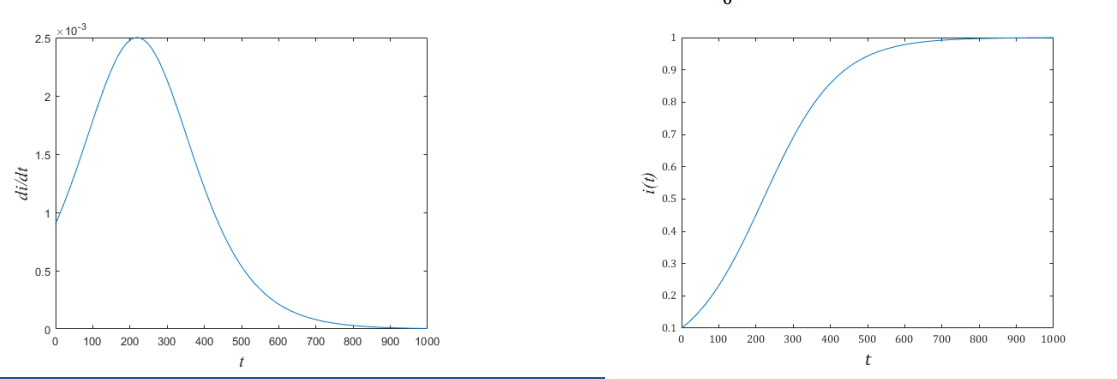
• 医学上
称d𝑖(𝑡)/d𝑡为传染病曲线
，表示
传染病人增加率与时间的关系
，如左图所示
• 预测结果如右图所示，随着时间的推移，病人比例接近100%
• 当病人总量占总人口比值达到50%，即
i = 0.5时，di/d𝑡达到最大值
，此时为
传染高峰期
• 根据i(t)的表达式，可得
高峰期对应时刻
❑ 结果意义
•
高峰期对应时刻
：
医学上该结果具有
重要意义
•
提前预防
：若已知日接触率（统计调查等），可预测高峰期到来的时间t𝑚，做好应对准备
• 由于t𝑚与
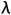
成反比，若能
减小
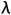
（隔离、戴口罩等），则t𝑚将变大
• 也就意味着传染病
高峰期来得越晚
，现实中可能在高峰期到来之前就彻底解决了该传染病
• 注意：比赛时需要
根据数学结果，分析求解结果的现实意义
，写进论文
•
但SI模型中未考虑病人得病后可以治愈
，𝑡 → ∞时𝑖(𝑡) → 1，即最后所有人都被传染
• 问题源自模型假设中只有健康者变为病人，但病人不会变为健康者，显然不合理
• 进一步分析问题，可建立SIS模型
•
SIS模型与SIR模型
❑SIS模型
❑ 模型改进
•
SI模型中未考虑病人得病后可以治愈
，𝑡 → ∞时i(𝑡) → 1，即最后所有人都被传染
• 问题源自模型假设中只有健康者变为病人，但病人不会变为健康者，显然不合理
• 因此，
需要同时考虑
传染
和
治愈
• 基于以上分析，对模型进行改进，建立SIS模型
❑ SIS模型
• SIS模型
在SI模型假设的基础上
，进一步假设：
1、
治愈比例
：每天被治愈的病人人数占病人总数的比例为μ
2、
无免疫性
：病人被治愈后成为仍可被感染的健康者
• 得到SIS模型：
• 可见，SIS模型是比原SI模型多了一项“ − 𝜇𝑖(t)”
❑ SIS模型解析解
• 该模型的解析解为：
• 令
为
传染强度
（病人日接触率/病人每日被治愈比例）
• 带入上一页模型的公式，得微分方程和解析解：
❑ 结果分析
❑ 显然，
传染强度
为一个阈值
• 若
≤ 1，
现实意义
“病人日接触率≤病人每日被治愈比例”
• 即
新增病人少于被治愈病人
，
那么随着t→ ∞，终所有病人都会被治愈
• 若
> 1 ，
现实意义
“病人日接触率>病人每日被治愈比例”
• 即
新增病人多于被治愈病人
，
那么随着t → ∞，总有一定比例的人口会被传染成病人
❑ SIR模型
❑ 模型改进
• 上页分析是建立在假设“无免疫性：病人被治愈后成为仍可被感染的健康者”的基础上
• 进一步考虑现实中天花、麻疹、流感、肝炎等疾病经治愈后均有很强的免疫力
•
病愈后的人因已具有免疫力
，既非易感染者也非病人（已感染者），即这部分人已退出感染
系统，再也不会被感染成患者
• 因此，考虑免疫性，
改进为SIR模型
❑ 模型假设
1
、人群分
易染者
(Susceptible)、
病人
(Infective)和病愈后有免疫力而退出系统的
移出者
(Removal)
2
、设任意时刻𝑡，这三类人群占总人口的比例分别为s(𝑡), 𝑖(𝑡)和𝑟(𝑡) 。
3、病人的日接触率为λ，日治愈率为𝜇
4、人口总数𝑁为固定常数，既不考虑生死，也不考虑迁移
❑ 模型的建立
• 对于全体人群： s(t)+i(t)+r(t)=1
• 对于移出者： （右式根据定义得出）
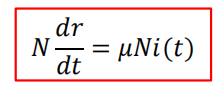
，即移出者人数的变化率是单位时间被治愈的患者数
• 对于患者：
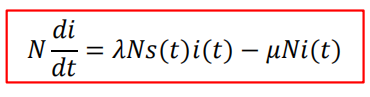
• 对于健康者：
• 根据以上分析，建立微分方程传染病预测SIR模型
❑ 模型分析
• SIR模型形式是
多个相互关联
的
系统变量
之间的
常微分方程组
，属于典型的
系统动力学模型
• 更复杂的情况，考虑有些传染病具有潜伏期，考虑一类人为潜伏者，建立SEIR模型
• 类似的问题：河流各类污染物质的耗氧、复氧、吸附、沉降等
• 该类问题往往
难以求得精确的解析解
，可以使用MATLAB求数值解
•
代码求解微分方程数值解
❑代码求解
求解微分方程
• MATLAB提供了通用的求常微分方程数值解的函数ode45
• 基本语法：
https://ww2.mathworks.cn/help/matlab/ref/ode45.html?s_tid=srchtitle_ode45_1#d123e934673
• 预测结果：
clc,clear
% 参数初始化
lam = 0.4; % 日接触率，题中若没给出需要自己查资料，后面同理
mu = 0.1; % 日治愈率
I = 0.4;
S = 0.5;
% ode45是一个通用型ODE求解器
tspan = [0:1:50]; % 变量t范围0到50
y0 = [I S]; % 传递模型参数，SIR相加等于一求两个即可得出第三个
调用ode45
首先是待求解的微分方程
，在MATLAB中定义为函数SIRfunc（其表达式在本文件末尾分节后），还有传递给该函数的参数t和y，以“@(t,y)SIRfunc(t,y,lam,mu)”的形式表达。
其次是积分区间
，以tspan表示，是个矩阵，包括积分区间的左右端点数值。如果要获取 t0 到 tf 之间的特定时间的解，使用 [t0,t1,t2,…,tf] 形式的长向量
最后是初始值
，用向量y0表示。
本题先求解微分方程：
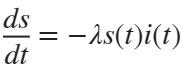
求出i和s后，根据s(t)+i(t)+r(t)=1可直接求出r
[t,y] = ode45(@(t,y)SIRfunc(t,y,lam,mu), tspan, y0); %注意ode45的语法
% 求解返回的y中，第一列是第一个方程组的解，第二列是第二个微分方程的解
r = 1-y(:,1)-y(:,2); % 移出者的比例
%画图
plot(t,y(:,1),t,y(:,2),t,r,'k','LineWidth',2);
legend('患病:i(t)','易感染者:s(t)','移除者:r(t)','Location','Best');
ylabel('占人口比例%');
xlabel('时间t');
title('SIR模型(ode)');
function dydt = SIRfunc(t,y,lam,mu)
dydt = zeros(2,1);
dydt(1) = lam*y(1)*y(2) - mu*y(1);
dydt(2) = -lam*y(1)*y(2);
end