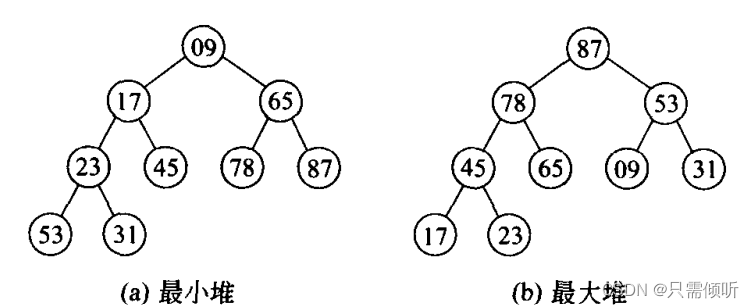
1.最小堆的结构：

左右子女的元素均小于等于父节点的元素，叫最小堆；左右子女的元素均大于等于父节点的元素，叫最大堆。

2.最小堆的建立过程如下图所示：

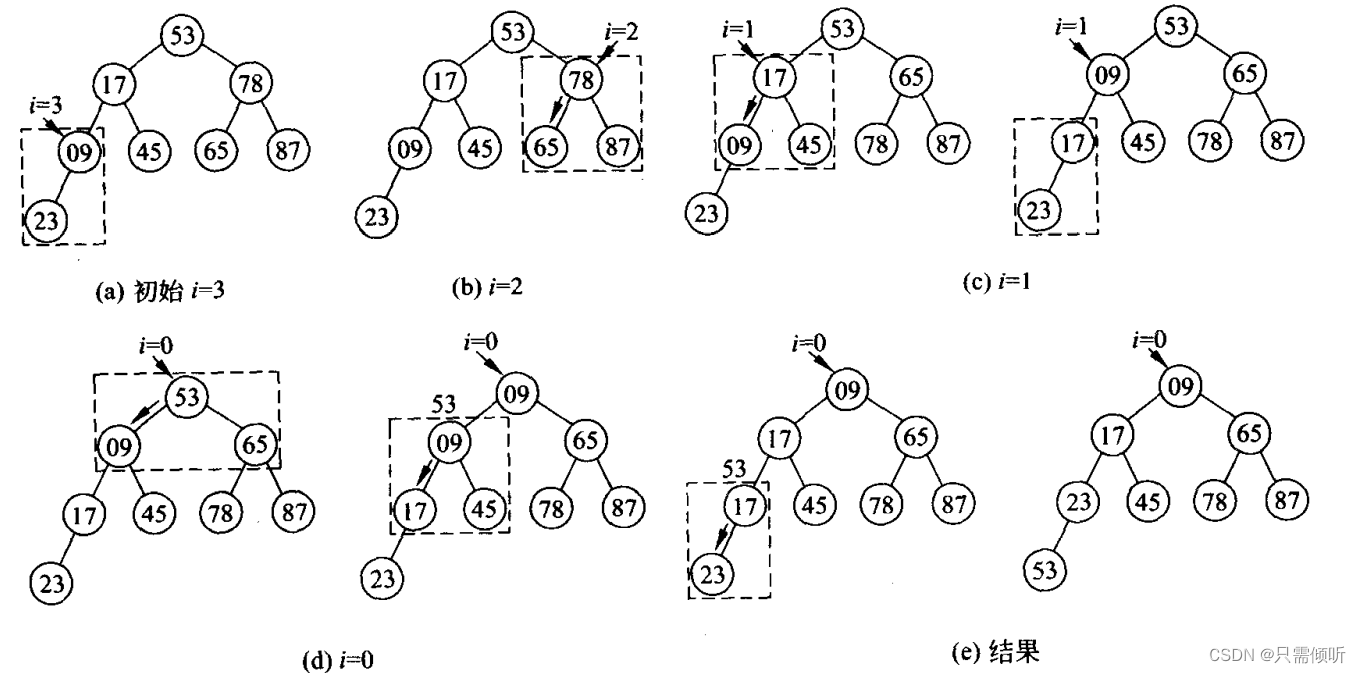
所有节点从上往下，从左往右一次标号0,1,2，…,。 从最后一个拥有子女的父节点开始，比较父节点与左右子女的元素（也可以叫关键码）的大小，如果父节点的关键码比左右子女的都小或小于等于，则不作调整，如上图图（a）；父节点的关键码与子女中关键码小的子女的关键码大，则父节点的关键码与小的子女关键码进行交换。

关于标号的二叉树知识：对于所有的节点，依次标号0,1,2，…，n，对于任意标号为

i

的节点，其左子女标号为

2i+1

，右子女标号为

2i+2

（如果有左右子女的话）。这样就可以根据下标知道任意节点的父节点及其左右子女节点的小标（如果有的话）。因此，不再需要使用链表进行指定父节点或子女节点的地址，因此堆的存储就可以使用数组，

只要知道下标 i，就知道其父节点的坐标

向下取整，左子女节点下标 2i+1，有子女下标 2i+2。特殊之处就是树的根节点没有父节点，不需要求


。

堆的空间结构是二叉树，物理存储是数组。

本文的代码输入的堆元素的关键码也是根据二叉树的结构从上往下、从左往右的顺序，依次存入数组中，标号为0,1,2，…，n，最小堆的调整也是根据空间结构，通过数组下标实现关键码的交换，以形成最小堆。最小堆最大堆方法类似，本文以最小队为例利用C++进行实现。

3.MinHeap的头文件，定义最小堆的类模板集贤关接口，代码如下：

#pragma once
# include<iostream>
using namespace std;

int DefaultSize = 10;  //定义最小堆默认存储数据的数目

//最小堆的头文件，包括类定义及接口的实现。
template <class T>
class MinHeap
{
public:
	MinHeap(int sz = DefaultSize);		//构造函数，建立空堆
	MinHeap(T arr[], int n);			//构造函数，通过一个数组建立堆,这个数组有n个元素
	~MinHeap() { delete[] heap; }		//析构函数

	bool Insert(const T& x);			//将新元素的关键码x插入到最小堆中
	bool Remove(T &x);					//删除堆顶的最小元素
	bool IsEmpty() const { return (currentSize == 0) ? true : false; }
	bool IsFull() const { (currentSize == maxHeapSize) ? true : false; }
	void MakeEmpty() { currentSize = 0; }   //内存并没有释放
	template<class R>
	friend ostream& operator<<(ostream&out, MinHeap<R> & hp);

private:
	T * heap;							//存放最小堆中元素关键码的数组
	int currentSize;					//最小堆中当前元素的个数
	int maxHeapSize;					//最小堆最多允许的元素个数
	void siftDown(int start, int m);	//从start到m下滑调整成为最小堆
	void siftUp(int start);				//从start到0上滑调整成为最小堆
};

template<class T>
MinHeap<T>::MinHeap(int sz) //参数再写int sz = DefaultSize报错
{
	//maxHeapSize = (DefaultSize < sz) ? sz : DefaultSize;
	if (DefaultSize < sz)
		maxHeapSize = sz;
	else
		maxHeapSize = DefaultSize;

	heap = new T[maxHeapSize];          //创建堆存储空间(就是简单的数组)
	if (heap == nullptr)
	{
		cerr << "内存分配失败" << endl;
		exit(1);
	}
	currentSize = 0;
}

template<class T>
MinHeap<T>::MinHeap(T arr[], int n)
{
	//maxHeapSize = (DefaultSize < n) ? n : DefaultSize;  //若n>DefaultSize，则堆是满的；否则堆不满(默认数组没有空的内存，存满了数据)
	if (DefaultSize < n)
		maxHeapSize = n;
	else
		maxHeapSize = DefaultSize;

	heap = new T[maxHeapSize];
	if (heap == nullptr)
	{
		cerr << "内存分配失败！" << endl;
		exit(1);
	}

	//把数组arr复制到堆数组中
	for (int i = 0; i < n; i++)
	{
		heap[i] = arr[i];
	}

	currentSize = n;
	int currentPos = (currentSize - 1) / 2;		//找到最初调整的位置：最后拥有子女结点的结点即最后的那个父节点
	while (currentPos >= 0)                     //控制多次局部最小堆以实现全局都是最小堆
	{
		siftDown(currentPos, currentSize - 1);  //局部自上向下下滑调整。各个元素关键码的下表是从0开始算的，所以最后一个关键码的位置是currentSize - 1
		currentPos--;
	}
}

//最小堆的下滑调整算法（局部调整）
//虽然siftDown是私有权限，但是该权限是对对象而言的，类外实现的时候只需加作用域即可写代码实现该函数
template<class T>
void MinHeap<T>::siftDown(int start, int m)
{
	//从start结点开始到m节点位置，自上向下比较，如果子女的关键码小于父节点的关键码，则关键码小的上浮，继续往
	//下层比较，这样将以start为根节点的子树调整为局部的最小堆
	int i = start, j = 2 * i + 1;			//j是作左子女的位置

	while (j <= m)							//访问不超出m节点位置
	{
		if (j < m && heap[j + 1] < heap[j])
			j++;							//让j指向两子女的小者

		if (heap[j] > heap[i]) break;       //如果子女的关键码比父节点的大，则不做调整
		else  //关键码交换
		{
			T temp = heap[i];
			heap[i] = heap[j];				//小的关键码上浮
			i = j;							//更新根节点下表
			j = 2 * j + 1;					//新根节点的左子女下表
			heap[i] = temp;			        //大的关键码下沉到刚刚的子女位置
		}
	}

}

//最小堆的上滑调整算法,调整的是全局
template<class T>
void MinHeap<T>::siftUp(int start)
{
	//从start开始到结点0为止，自下向上比较，如果子女的关键码小于父节点的关键码，则相互交换。这样将集合重新调整为最小堆
	int j = start, i = (j - 1) / 2;			//和siftDown一样，j指向子女，i指向父节点

	while (j > 0)
	{
		if (heap[i] < heap[j]) break;		//如果父节点更小，则不用做调整
		else //关键码交换
		{
			T temp = heap[j];				//记录子女关键码
			heap[j] = heap[i];				//父节点关键码下移
			j = i;							//当前父节点作为上一层调整的子女结点
			i = (j - 1) / 2;				//新的父节点
			heap[j] = temp;					//小的关键码上浮
		}
	}

}

//插入元素的关键码总会放在已存在最小堆的最后面，然后将其与父节点的关键码进行比较，完成对调以形成新的最小堆
//关键码比较回调的过程用到了堆的上滑调整操作siftUp
template<class T>
bool MinHeap<T>::Insert(const T& x)
{
	//将新元素的关键码x插入到最小堆中
	if (currentSize == maxHeapSize)
	{
		cerr << "Heap Full!" << endl;
		return false;
	}

	heap[currentSize] = x;				//先将关键码放在堆的最后
	siftUp(currentSize);				//从最后的位置开始回调
	currentSize++;
	return true;
}


//删除堆顶的最小元素
template<class T>
bool MinHeap<T>::Remove(T &x)
{
	//删除堆顶的最小关键码后，一般以堆的最后一个元素填补该位置，并将currentSize减一。此时最小堆已被破坏，所以调用siftDown再次调整
	if (!currentSize)  //如果堆为空
	{
		cerr << "Heap Empty!" << endl;
		return false;
	}

	x = heap[0];							//取堆顶最小关键码
	heap[0] = heap[currentSize - 1];		//最后的关键码补顶
	heap[currentSize - 1] = x;				//堆顶的元素放在数组的后面，虽然下一句currentSize--后不能再输出该值，但是可以为堆排序做铺垫
	currentSize--;
	siftDown(0, currentSize - 1);			//从堆顶向下调整为堆
	return true;
}

//堆的存储形式为完全二叉树，按照完全二叉树从上往下，从左往右的顺序依次输出个元素的关键码
template<class R>
ostream& operator<<(ostream&out, MinHeap<R> & hp)
{
	if (hp.currentSize == 0)
	{
		out << "Heap Empty!" << endl;
	}
	else
	{
		for (int i = 0; i < hp.currentSize; i++)
			out << hp.heap[i] << " ";
	}
	out << endl;
	return out;
}

4.最小堆cpp文件，用于测试MinHeap头文件中的类模板及接口的功能，代码如下：

#include "MinHeap.h"
#include <iostream>
using namespace std;
int main()
{
	int arr[8] = { 53,17,78,9,45,65,87,23 };
	MinHeap<int> hp(arr, 8);
	cout << hp;
	hp.Insert(11);
	cout << hp;
	int x;
	hp.Remove(x);
	cout << hp;
	return 0;
}

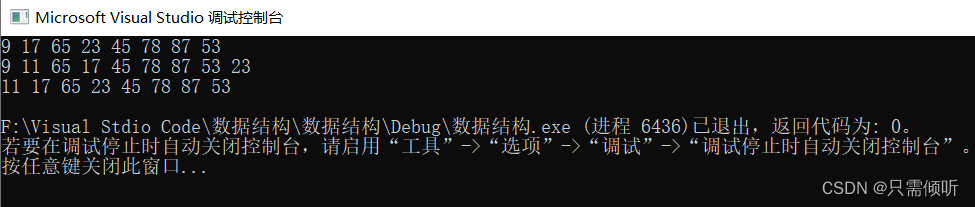
5.测试结果如图所示：堆输出的时候按照从上到下、从左到右的顺序依次输出：