目录
一、堆叠小卷积核
1.为什么要用大卷积核代替小卷积核?
-
大卷积核
- 优点:感受域范围大
- 举例:AlexNet、LeNet等网络都使用了比较大的卷积核,如5×5、11×11
- 缺点:参数量多:计算量大
-
小卷积核
- 优点:参数量少;计算量小;整合三个非线性激活层代替单一非线性激活层,增加模型判别能力
- 举例:VGG之后
- 缺点:感受域不足;深度堆叠卷积(也就是堆叠非线性激活),容易出现不可控的因素
2.为什么堆叠小卷积核参数量要比大卷积核少?
-
设输入尺寸为5×5×10,输出尺寸为1×1×10
-
参数计算:
- 1个5×5卷积:5×5×10×10 = 2500
- 2个3×3卷积:3×3×10×10×2 = 1800
- 相差约1.4倍
- 1个7×7卷积:7×7×10×10 = 4900
- 3个3×3卷积:3×3×10×10×3 = 2700
- 相差约1.8倍
-
参数计算:
3.输入输出图片通道数一致时堆叠小卷积核参数量才更小
这是为什么呢?
-
设输入尺寸为15×15×3,输出尺寸为11×11×64
- 1个5×5卷积:5×5×3×64 = 4800
- 2个3×3卷积:3×3×3×64+3×3×64×64 = 38592
- 相差约8倍
-
设输入尺寸为11×11×64,输出尺寸为7×7×64
- 1个5×5卷积:5×5×64×64 = 102400
- 2个3×3卷积:3×3×64×2 = 1152
- 相差约88.8倍
这就是解释了为什么很多网络的第一层使用的都是7×7的大卷积核接受输入图片,因为网络开头使用小卷积核进行下采样参数量会更大。
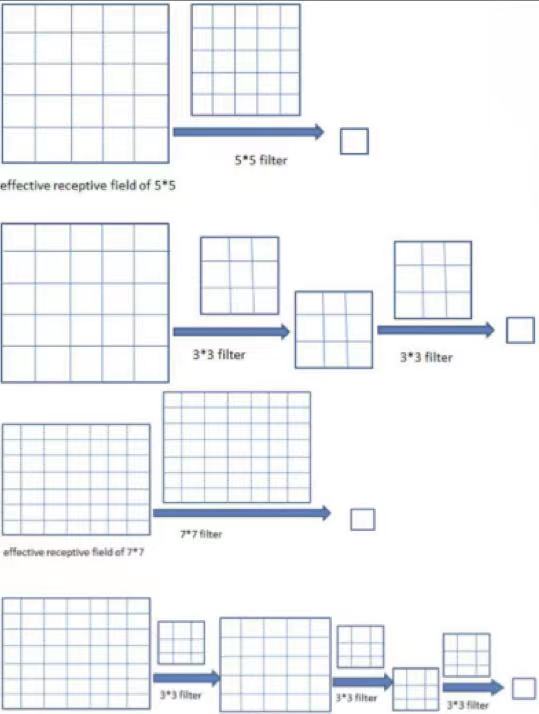
4.感受野计算
感受野的计算是
迭代计算
感受野计算公式:
1个5×5卷积:RF = 5
2个3×3卷积:RF = 3+(3-1)×1 = 5
1个7×7卷积:RF = 7
3个3×3卷积:RF = 3+(3-1)×1+(3-1)×1 = 7

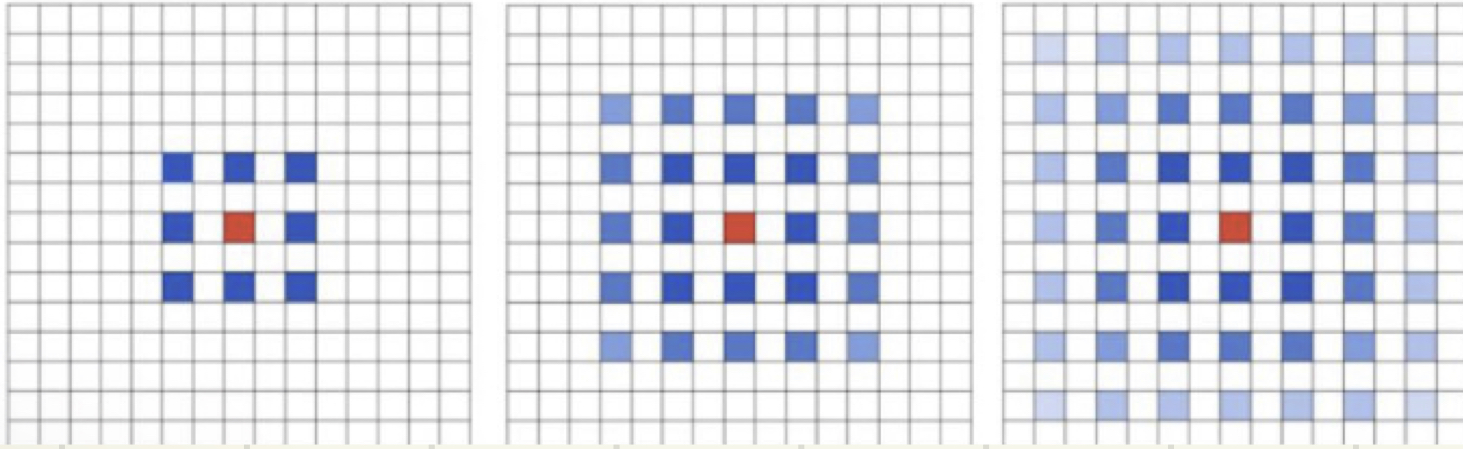
二、空洞卷积:能否让固定大小的卷积核看到更大范围的区域?
标准的3×3卷积核只能看到对应区域3×3的大小,但是为了能让卷积核看到更大的范围,dilated conv使其成为了可能。pooling下采样操作导致的信息丢失是不可逆的,这不利于像素级任务,用空洞卷积代替pooling的作用(成倍的增加感受野)更适用于语义分割。
举例:ASPP
关于空洞卷积感受野的计算请见:
空洞卷积
三、非对称卷积:卷积核一定是正方形吗?
将标准3×3卷积分成一个1×3卷积和3×1卷积,在不改变感受野大小的情况下可减少计算量
标准卷积计算量:9×9 = 81次乘法
非对称卷积计算量:3×15+3×9 = 72次乘法
注意:非对称卷积用在分辨率为12-20大小的特征图上效果会比较好
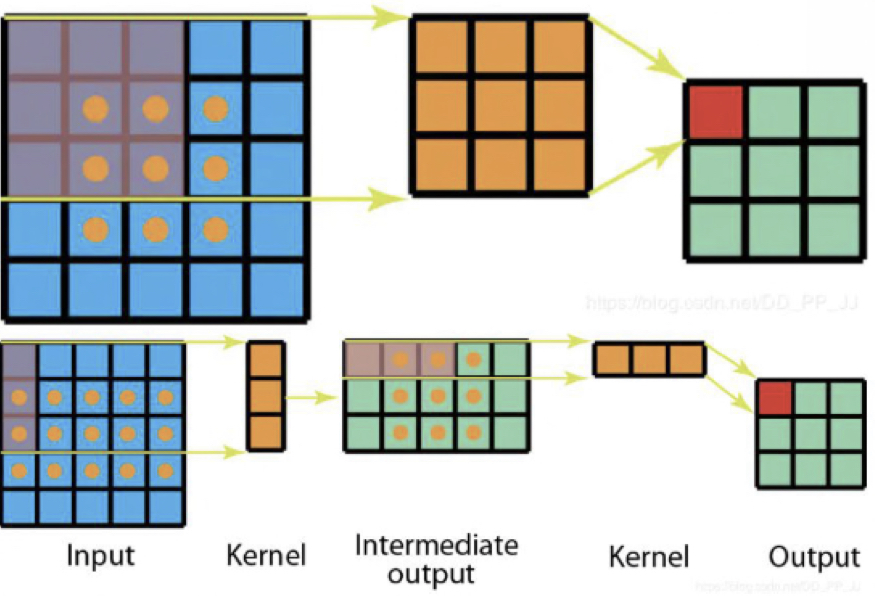
标准卷积与非对称卷积感受野对比

四、深度可分离卷积
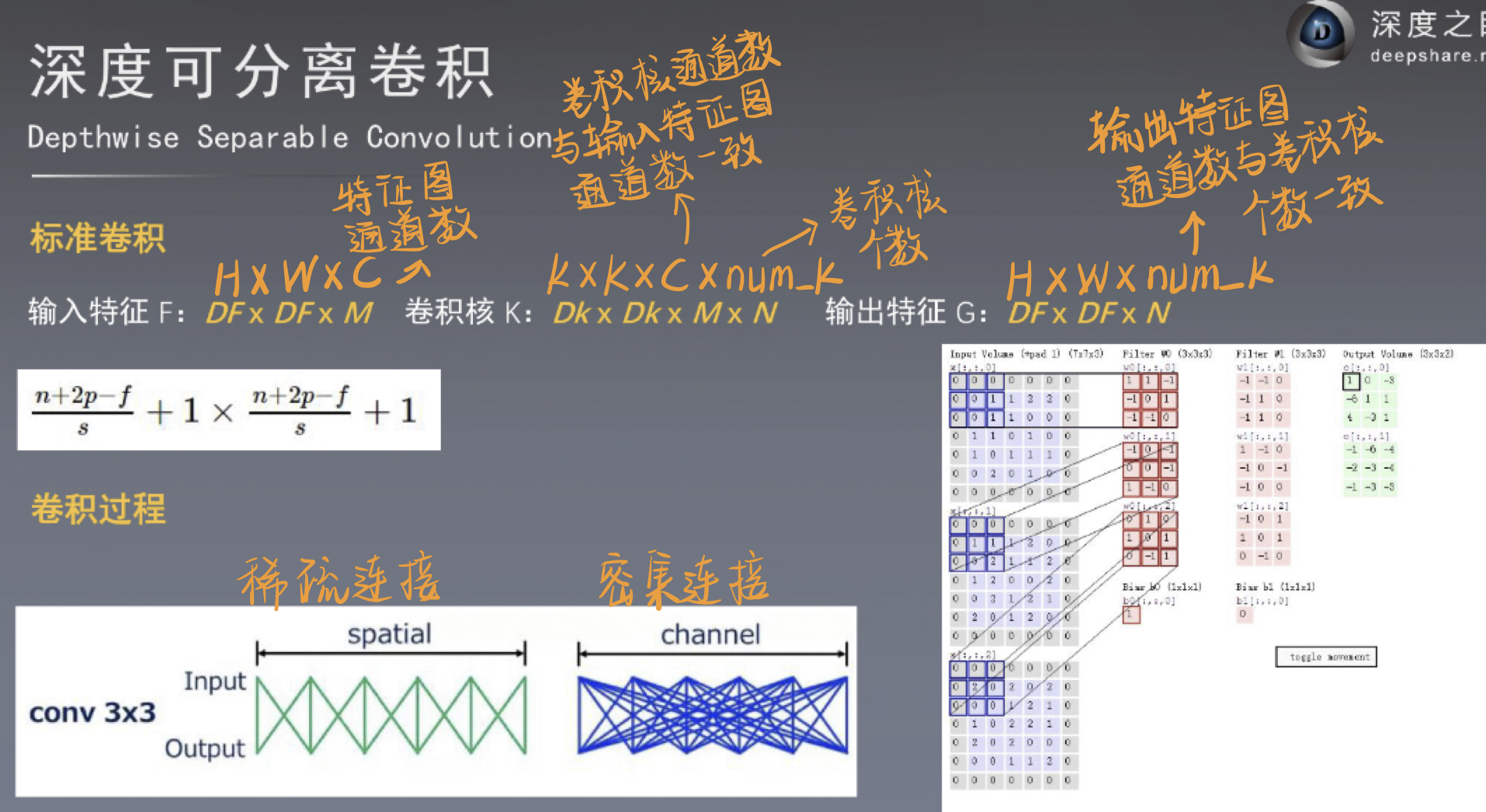
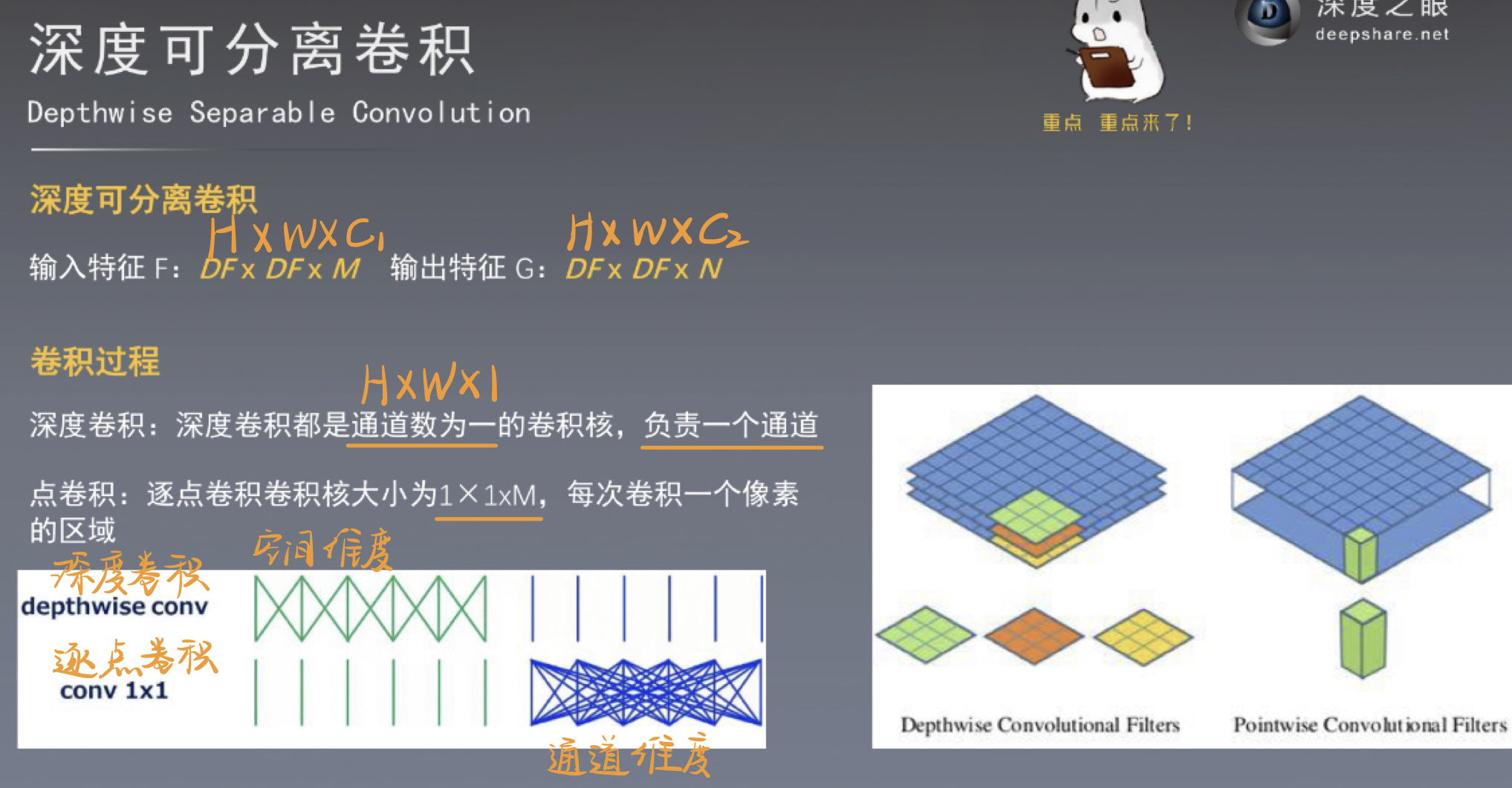

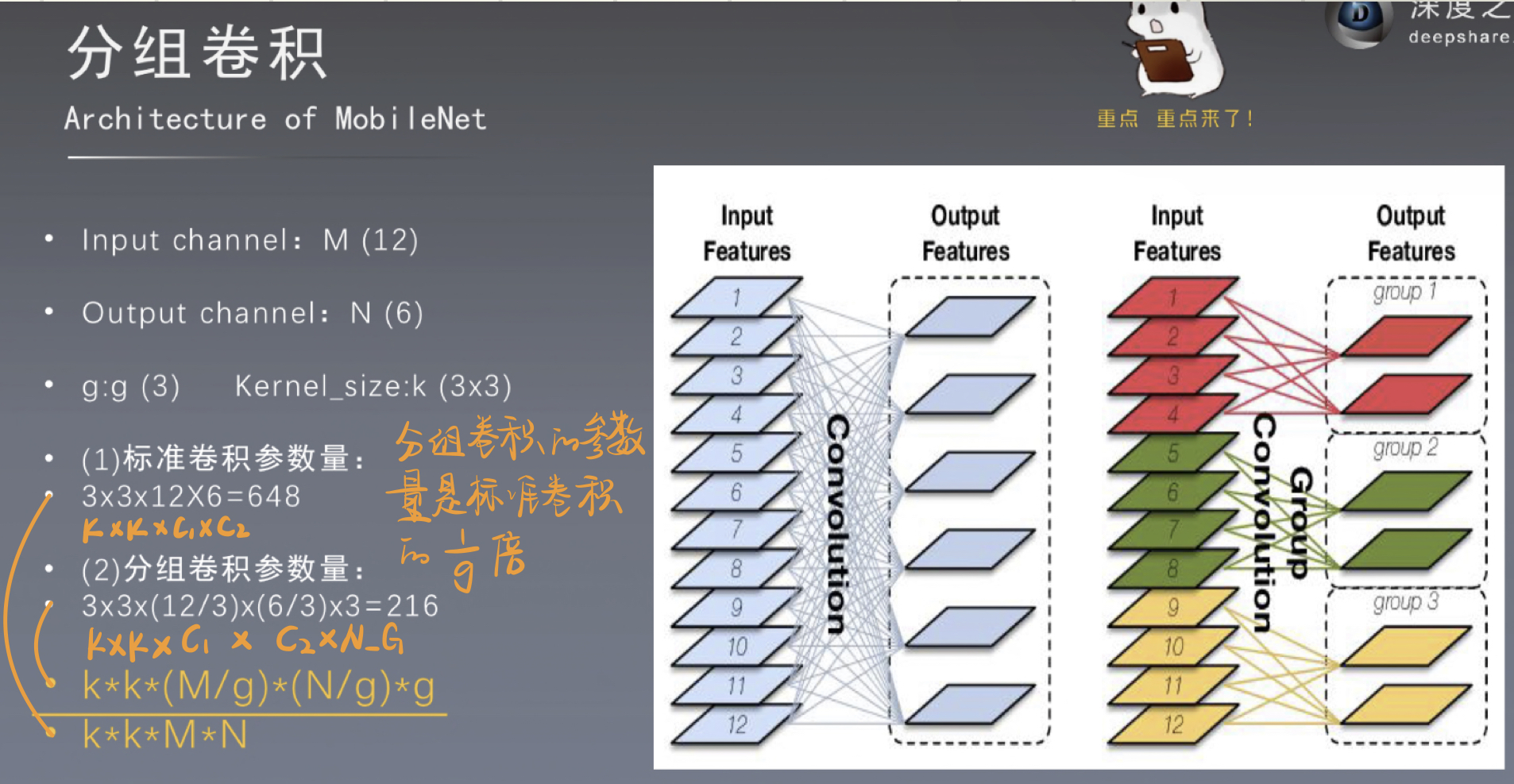
五、分组卷积:卷积只能在同一组进行吗?
组卷积是对输入特征图进行分组,每组分别进行卷积。假设输入特征图的尺寸为
C*H*W(12×5×5),
输出特征图的数量为
N(6)个
,如果设定要分成
G(3)个groups
,则每组的输入特征图数量为
C/G(4)
,每组的输出特征图数量为
N/G(2)
,每个卷积核的尺寸为
(C/G)*K*K(4×5×5)
,卷积核总数仍为
N(6)
个,每组的卷积核数量为
N/G(2)
,每个卷积核只与其同组的输入特征图进行卷积,卷积核的总参数量为
N*(C/G)*K*K
,可见,总参数量减少为原来的
1/G
。
举例:ResNext
缺点:分组点卷积某个通道仅来自一小部分输入通道,
阻止了信息流动,特征表示

分组卷积能否对通道进行随机分组?
为达到特征之间的互相通信,除了采用dense pointwise convolution,还可以使用channel shuffle。如图b所示,就是对group convolution之后的特征图进行“重组”,这样可以保证下面的卷积其输入来自不同的组,因此信息可以在不同组之间流转。图c进一步的展示了这一过程,相当于“均匀的打乱”。
举例:ShuffleNet


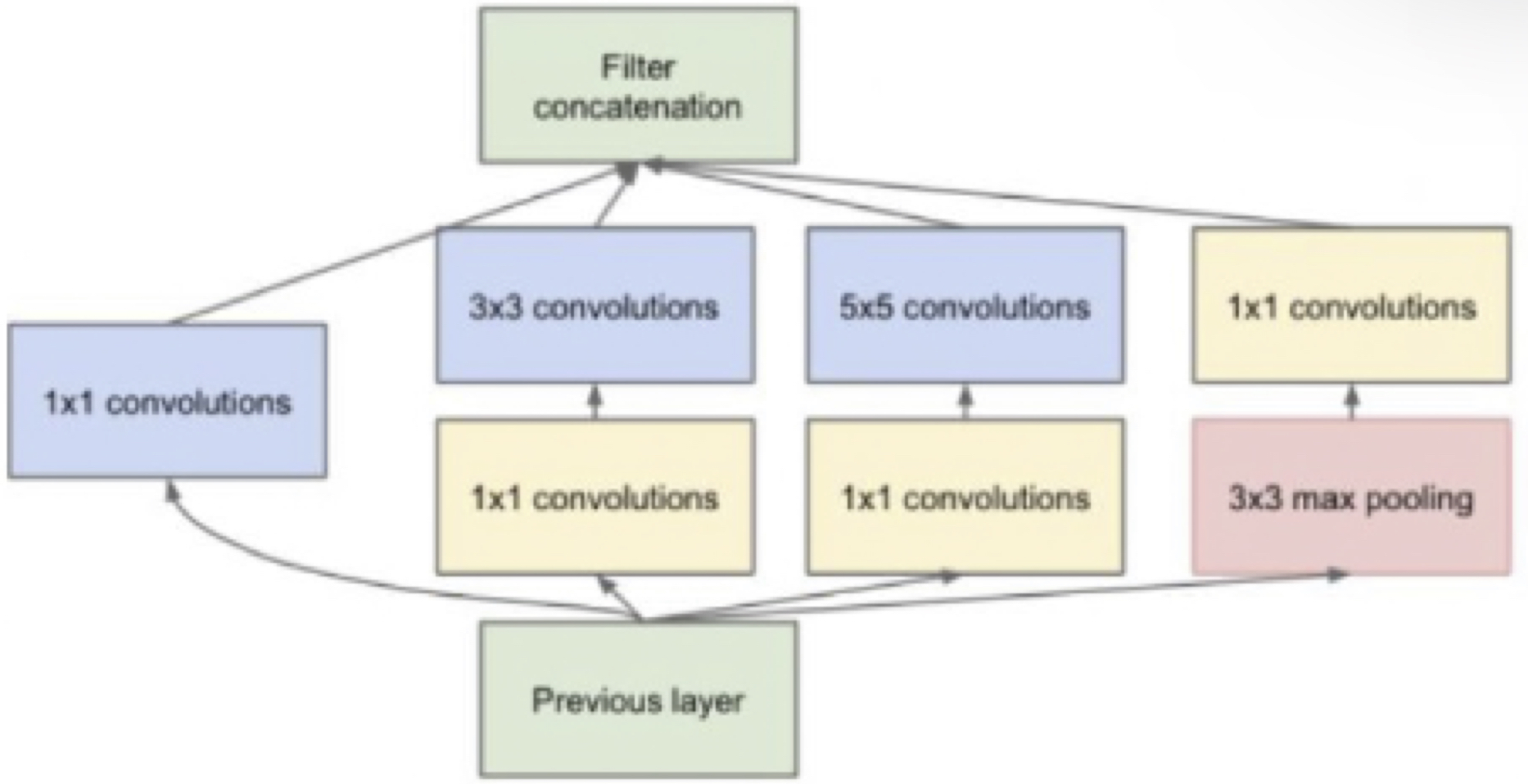
六、拓展卷积:每层卷积只能用一种尺寸的卷积核吗?
传统的层叠式网络,基本上都是一个个卷积层的堆叠,每层只用一个尺寸的卷积核,例如VGG结构中使用了大量的3×3卷积层。事实上,同一层feature map
可以分别使用多个不同尺寸的卷积核
,
以获得不同尺度的特征,
再把这些特征结合起来,得到的特征往往比使用单一卷积核的要好,
为了尽可能的减少参数,一般先用1×1的卷积将特征图映射到隐空间,再在隐空间做卷积
。
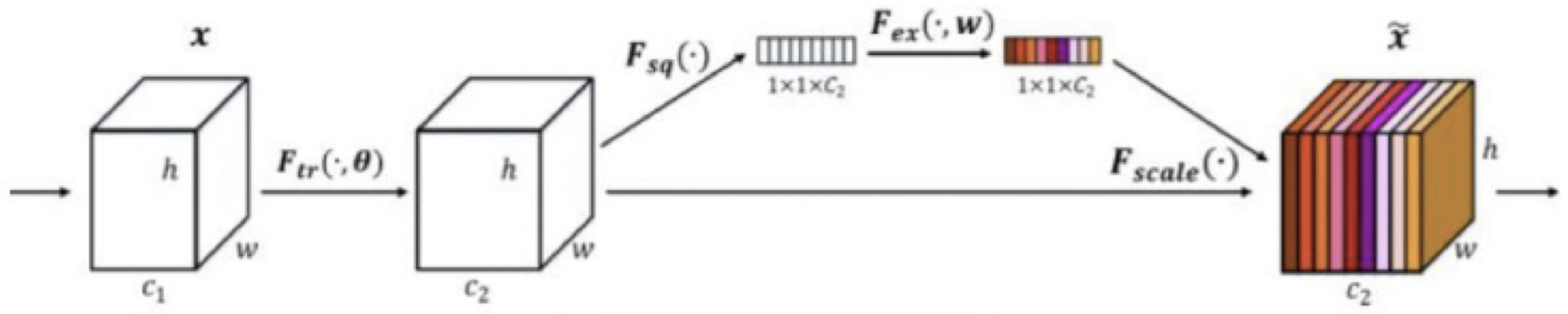
七、通道注意力:通道间的特征都是平等的吗?
无论是在Inception、DenseNet或者ShuffleNet里面,我们对所有通道产生的特征都是
不分权重直接结合的
,那为什么要认为所有通道的特征对模型的作用都是相等的呢?一个卷积层中往往有数以千计的卷积核,每个卷积核都对应了特征,于是那么多特征要怎区分?这个方法就是通过学习的方式来
自动获取到每个特征通道的重要程度
,然后
依照计算出来的重要程度去提升有用的特征并抑制对当前任务用处不大的特征
。
举例:SENet
八、可变性卷积:卷积核形状一定是矩形吗?
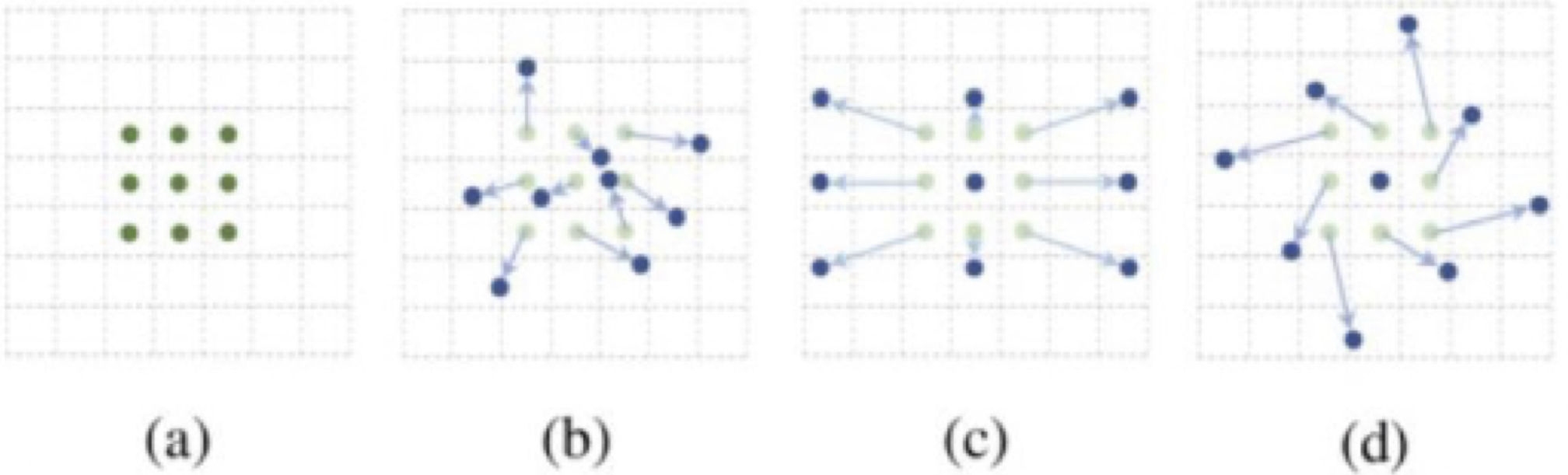
规则形状的卷积核(比如一般用的正方形3×3卷积)可能会限制特征的提取,如果
赋予卷积核形变的特征
,
让网络根据label反传下来的误差自动的调整卷积核的形状
,
适应网络重点关注的感兴趣的区域
,就可以提取更好的特征。例如,网络会根据原位置(a),学习一个offset偏移量,得到新的卷积核(b)(c)(d),那么一些特殊情况就会成为这个更泛化的模型的特例,例如图(c)表示从不同尺度物体的识别,图(d)表示旋转物体的识别。
缺点:由于需要计算卷积核的偏移量,故其
参数量会有一定增加。
举例:该方法多用于目标检测
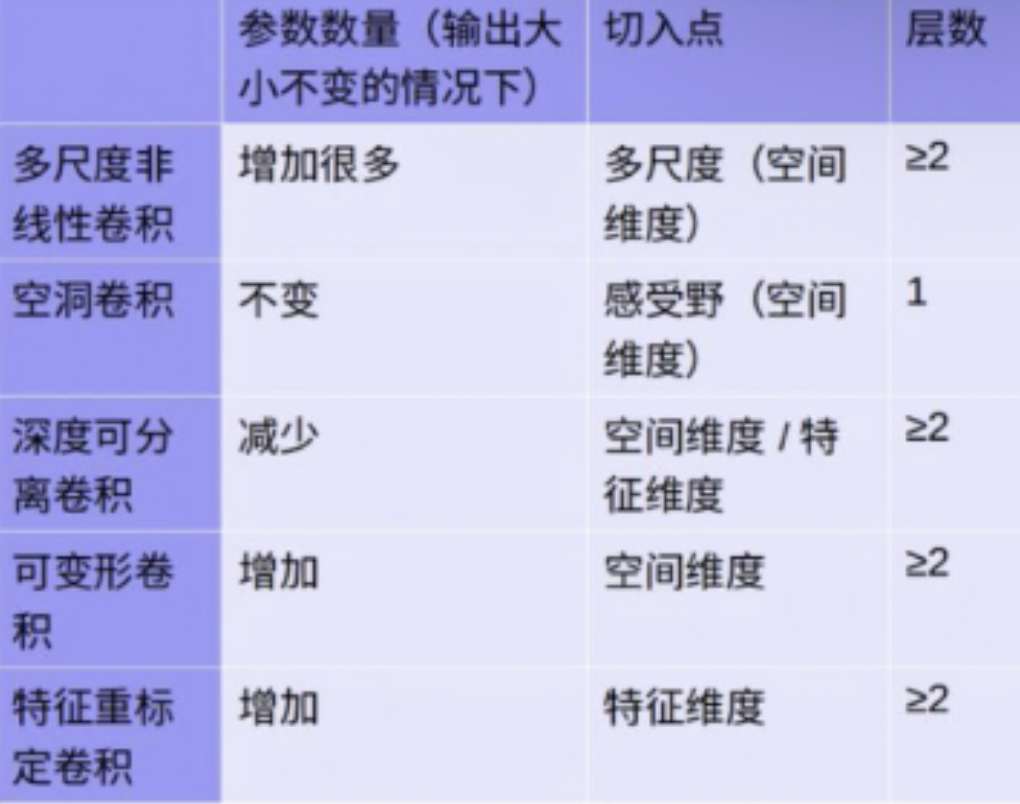
九、总结
1.卷积核方面
- 大卷积核用多个小卷积核代替
- 单一尺寸卷积核用多尺寸卷积核代替
- 固定形状卷积核趋于使用可变性卷积核
- 使用1×1卷积核(bottleneck结构)
2.卷积层通道方面
- 标准卷积用depthwise卷积代替
- 使用分组卷积
- 分组卷积后使用channel shuffle
- 通道加权计算
3.卷积层连接方面
- 使用skip connection,让模型更深(ResNet)
- densely connection,使每一层都融合其他层的特征输出(DenseNet)