博客

汇总篇：

计算几何汇总

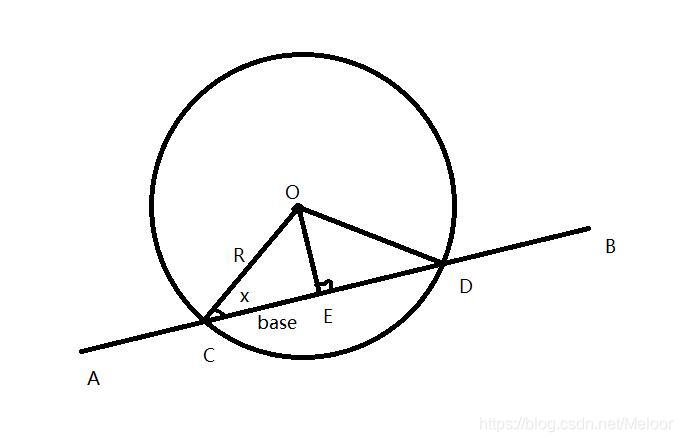
首先，求出圆心O在直线AB上的投影点E

然后求出

AB

的方向向量e=AB/|AB|

令EC=ED=base

base = sqrt(r^2-OE^2)

EC = -base *e

ED = base*e

C=E+EC

D=E+ED

相切时求得的C=D,CDE重合

如果A为切点，那么ACDE重合

#include<cmath>
const int eps = 1e-2;//精度
double myRound(double a){//因为小数有误差，所以判断相切时要精确到固定位数 
	return floor(a * 100 + 0.5) / 100; /*保留小数点后2位*/
}
class point{
 	public:
	double x;
	double y;
	point(double x_=0,double y_=0){
		x=x_;
		y=y_;
	} 
	void set(point p){
		x=p.x;
		y=p.y;
	}
	friend const point operator+(const point& p1,const point& p2){
		return point(p1.x+p2.x,p1.y+p2.y);
	};
	friend const point operator-(const point& p1,const point& p2){
		return point(p1.x-p2.x,p1.y-p2.y);
	};
	friend const point operator*(const point& p,const double& m){
		return point(p.x*m,p.y*m);
	};
	friend const point operator*(const double& m,const point& p){
		return point(p.x*m,p.y*m);
	};
	friend const point operator/(const point& p,const double& m){
		return point(p.x/m,p.y/m);
	};
	//friend ostream& operator <<(ostream& out,point& a);
};
typedef point vect2;//重命名，向量也是用坐标表示 

class line{
	public:
	point start;
	point end; 
	line(point s,point e){
		start.set(s);
		end.set(e);
	}
};

double dot(point O,point A,point B){//点乘 
	double oa_x=A.x-O.x;
	double oa_y=A.y-O.y;
	double ob_x=B.x-O.x;
	double ob_y=B.y-O.y;
	return oa_x*ob_x+oa_y*ob_y;
}
double dis(const point &p1,const point &p2){//求两点之间距离
	double ans=(p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y);
	return sqrt(ans);
}
double dis2(const point &p1,const point &p2){//求两点之间距离 
	return(p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y);	 
}
//点到直线的距离 
double disOfPointToLine(point O,line l){
	double cos0=dot(l.start,O,l.end)/(dis(O,l.start)*dis(l.start,l.end));
	return dis(O,l.start)*sin(acos(cos0));		
} 
//点在直线上的投影  
point shadowPointOfPointToLine(point A,line l){//投影点出了问题 
	point B = l.start;
	point C = l.end;
	point D;
	vect2 BC = C - B;
	vect2 BA = B - A;
	vect2 BD = dot(B,A,C)/dis2(B,C)*BC; 
	D = B + BD;
	return D;	
} 
//直线到圆的交点,所需函数：点到直线的距离，点在直线上的投影,两点之间的距离,判断点是否在线段上 
bool interPointOfLineAndCircle(line l,point O,double r,vector<point> &ans){
	ans.clear();
	point C,D,E;
	double d= disOfPointToLine(O,l);	
	E = shadowPointOfPointToLine(O,l);		
	vect2 AB = l.end-l.start;
	vect2 e=AB/dis(l.start,l.end);
	double base2 =myRound(r*r-d*d);//取约数，不然本来是0的会得不到0 
	//相切base^2 =0 两个点相等,相离 base^2<0 
	if(base2<0)return false;
	double base = sqrt(base2);	
	C = E - e*base;
	D = E + e*base;
	ans.push_back(C);
	if(!(D.x==C.x&&D.y==C.y))//避免点重复 
		ans.push_back(D);
	if(ans.size()>0)return true;
	else return false;		
}
//线段到圆的交点,所需函数：点到直线的距离，点在直线上的投影,两点之间的距离,判断点是否在线段上 
bool interPointOfLineAndCircle(line l,point O,double r,vector<point> &ans){
	ans.clear();
	point C,D,E;
	double d= disOfPointToLine(O,l);	
	E = shadowPointOfPointToLine(O,l);		
	vect2 AB = l.end-l.start;
	vect2 e=AB/dis(l.start,l.end);
	double base2 =myRound(r*r-d*d);//取约数，不然本来是0的会得不到0 
	//相切base^2 =0 两个点相等,相离 base^2<0 
	if(base2<0)return false;
	double base = sqrt(base2);	
	C = E - e*base;
	D = E + e*base;
	//判断C,D时候在线段AB上即可 
	if(pointIsOnLine(C,l))ans.push_back(C);
	if(pointIsOnLine(D,l)&&!(D.x==C.x&&D.y==C.y))//避免点重复 
		ans.push_back(D);
	if(ans.size()>0)return true;
	else return false;		
}