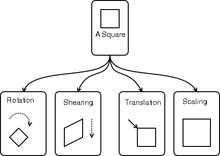
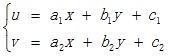图像映射

图像映射就是图像之间的变换，加上使用一些计算变换的方法。可以实现图像扭曲变形和图像配准，适用于全景拼接。普遍变换方法有单应性变换、仿射变换、阿尔法通道等等。图像的映射类型有：平移、旋转、仿射、透视映射、尺度变换，不同的类型对应不一样的方法。经过这些处理就可以达到自己想要实现的映射效果。

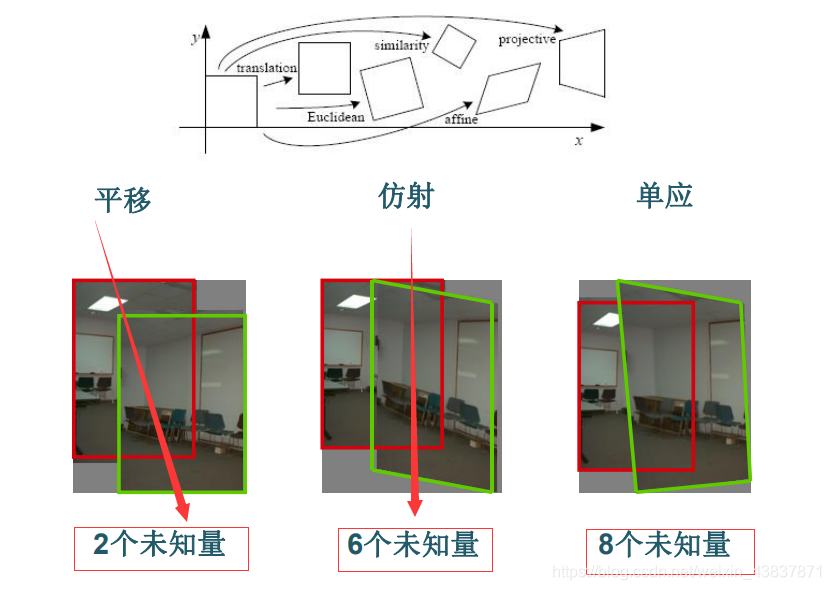
（一）原理解析

（1）单应性变换（homography）

矩阵的一个重要作用是将空间中的点变换到另一个空间中。比较形像直观地理解的方法就是图像变换，图像变换的方法很多，单应性变换是其中一种方法，单应性变换会涉及到单应性矩阵。单应性变换的目标是通过给定的几个点（通常是4对点）来得到单应性矩阵。以下为单应性矩阵的推导过程。

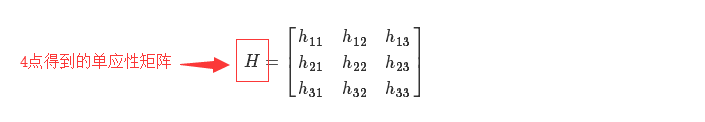
单应性矩阵

H

仅依赖尺度定义，所以，单应性矩阵具有

8

个独立自由度。通常会使第三个值为一来归一化点，即 ：

a

点坐标（x , y , z ) 转换成

a’

（x , y , 1）这样，点就具有唯一的图像坐标

x

和

y

。这个额外的坐标使得我们可以简单使用一个矩阵来表示表换。例如：矩阵H会将一幅图像上的一个点的坐标

a

=(x,y,1)映射成另一幅图像上的点的坐标

b

=(x1,y1,1)，已知

a

和

b

，它们是在同一平面上。 则有下面的公式：

即：

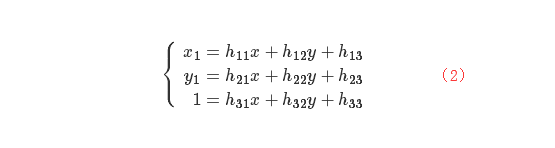
由上面的公式

1=h31x+h32y+h331 可得到：

然后取

V

的最后一列出来作为求解hh。因为矩阵

A

是行满秩，即只有一个自由度。具体实现需要输入两张图片，在两张图片之间找到4个点坐标，由此得到矩阵H。

（2）仿射变换

仿射变换（Affine Transformation ）是一种二维坐标（x, y）到二维坐标（u, v）的线性变换，保持二维图形的”平直性”(即变换后直线还是直线不会打弯，圆弧还是圆弧)和”平行性”(译注:par

常用的仿射变换:旋转、倾斜、平移、缩放

allelness，指保持二维图形间的相对位置关系不变，平行线还是平行线，而直线上点的位置顺序不变，需要注意向量间夹角可能会发生变化)。由于仿射变换具有6个自由度，因此需要三个对应点对估计矩阵H。通过最后两个元素设置为0，再通过直接线性变换（DLT）估计算出。可以通过Haffine_from_points(fp,tp)函数使用对应点对来计算仿射变换矩阵。其线性表达式形式如下：

对应的齐次坐标矩阵表示形式为：此类变换可以用一个3×3的矩阵来表示，其最后一行为(0, 0, 1)。该变换矩阵将原坐标(x, y)变换为新坐标(x’, y’)，这里原坐标和新坐标皆视为最末一行为(1)的三维列向量，原列向量左乘变换矩阵得到新的列向量:

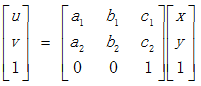
（3）alpha通道

阿尔法

通道

是一个8位的灰度通道，该通道用256级灰度来记录图像中的透明度信息，定义透明、不透明和半透明区域，其中白表示不透明，黑表示透明，灰表示半透明。

（二）仿射变换将一幅图像放置到另外一幅图像中

仿射扭曲im1到im3的例子：

 # -*- coding: utf-8 -*-
from PCV.geometry import warp, homography
from PIL import  Image
from pylab import *
from scipy import ndimage



# example of affine warp of im1 onto im2

im1 = array(Image.open('E.jpg').convert('L'))
im2 = array(Image.open('G.jpg').convert('L'))
# set to points
#tp = array([[120,260,260,120],[16,16,305,305],[1,1,1,1]])
tp = array([[600,2250,2550,600],[500,500,2400,2400],[1,1,1,1]])
im3 = warp.image_in_image(im1,im2,tp)
figure()
gray()
subplot(141)
axis('off')
imshow(im1)
subplot(142)
axis('off')
imshow(im2)
subplot(143)
axis('off')
imshow(im3)

# set from points to corners of im1
m,n = im1.shape[:2]
fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
# first triangle
tp2 = tp[:,:3]
fp2 = fp[:,:3]
# compute H
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im3 = (1-alpha)*im2 + alpha*im1_t
# second triangle
tp2 = tp[:,[0,2,3]]
fp2 = fp[:,[0,2,3]]
# compute H
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im4 = (1-alpha)*im3 + alpha*im1_t
subplot(144)
imshow(im4)
axis('off')
show()

warp.py.

from scipy.spatial import Delaunay 
from scipy import ndimage
from pylab import *
from numpy import *

from PCV.geometry import homography
    

def image_in_image(im1,im2,tp):
    """ Put im1 in im2 with an affine transformation
        such that corners are as close to tp as possible.
        tp are homogeneous and counter-clockwise from top left. """ 
    
    # points to warp from
    m,n = im1.shape[:2]
    fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
    
    # compute affine transform and apply
    H = homography.Haffine_from_points(tp,fp)
    im1_t = ndimage.affine_transform(im1,H[:2,:2],
                    (H[0,2],H[1,2]),im2.shape[:2])
    alpha = (im1_t > 0)
    
    return (1-alpha)*im2 + alpha*im1_t


def combine_images(im1,im2,alpha):
    """ Blend two images with weights as in alpha. """
    return (1-alpha)*im1 + alpha*im2    
    

def alpha_for_triangle(points,m,n):
    """ Creates alpha map of size (m,n) 
        for a triangle with corners defined by points
        (given in normalized homogeneous coordinates). """
    
    alpha = zeros((m,n))
    for i in range(min(points[0]),max(points[0])):
        for j in range(min(points[1]),max(points[1])):
            x = linalg.solve(points,[i,j,1])
            if min(x) > 0: #all coefficients positive
                alpha[i,j] = 1
    return alpha
    

def triangulate_points(x,y):
    """ Delaunay triangulation of 2D points. """
    
    centers,edges,tri,neighbors = md.delaunay(x,y)
    return tri


def plot_mesh(x,y,tri):
    """ Plot triangles. """ 
    
    for t in tri:
        t_ext = [t[0], t[1], t[2], t[0]] # add first point to end
        plot(x[t_ext],y[t_ext],'r')


def pw_affine(fromim,toim,fp,tp,tri):
    """ Warp triangular patches from an image.
        fromim = image to warp 
        toim = destination image
        fp = from points in hom. coordinates
        tp = to points in hom.  coordinates
        tri = triangulation. """
                
    im = toim.copy()
    
    # check if image is grayscale or color
    is_color = len(fromim.shape) == 3
    
    # create image to warp to (needed if iterate colors)
    im_t = zeros(im.shape, 'uint8') 
    
    for t in tri:
        # compute affine transformation
        H = homography.Haffine_from_points(tp[:,t],fp[:,t])
        
        if is_color:
            for col in range(fromim.shape[2]):
                im_t[:,:,col] = ndimage.affine_transform(
                    fromim[:,:,col],H[:2,:2],(H[0,2],H[1,2]),im.shape[:2])
        else:
            im_t = ndimage.affine_transform(
                    fromim,H[:2,:2],(H[0,2],H[1,2]),im.shape[:2])
        
        # alpha for triangle
        alpha = alpha_for_triangle(tp[:,t],im.shape[0],im.shape[1])
        
        # add triangle to image
        im[alpha>0] = im_t[alpha>0]
        
    return im
    
    
def panorama(H,fromim,toim,padding=2400,delta=2400):
    """ Create horizontal panorama by blending two images 
        using a homography H (preferably estimated using RANSAC).
        The result is an image with the same height as toim. 'padding' 
        specifies number of fill pixels and 'delta' additional translation. """ 
    
    # check if images are grayscale or color
    is_color = len(fromim.shape) == 3
    
    # homography transformation for geometric_transform()
    def transf(p):
        p2 = dot(H,[p[0],p[1],1])
        return (p2[0]/p2[2],p2[1]/p2[2])
    
    if H[1,2]<0: # fromim is to the right
        print ('warp - right')
        # transform fromim
        if is_color:
            # pad the destination image with zeros to the right
            toim_t = hstack((toim,zeros((toim.shape[0],padding,3))))
            fromim_t = zeros((toim.shape[0],toim.shape[1]+padding,toim.shape[2]))
            for col in range(3):
                fromim_t[:,:,col] = ndimage.geometric_transform(fromim[:,:,col],
                                        transf,(toim.shape[0],toim.shape[1]+padding))
        else:
            # pad the destination image with zeros to the right
            toim_t = hstack((toim,zeros((toim.shape[0],padding))))
            fromim_t = ndimage.geometric_transform(fromim,transf,
                                    (toim.shape[0],toim.shape[1]+padding)) 
    else:
        print ('warp - left')
        # add translation to compensate for padding to the left
        H_delta = array([[1,0,0],[0,1,-delta],[0,0,1]])
        H = dot(H,H_delta)
        # transform fromim
        if is_color:
            # pad the destination image with zeros to the left
            toim_t = hstack((zeros((toim.shape[0],padding,3)),toim))
            fromim_t = zeros((toim.shape[0],toim.shape[1]+padding,toim.shape[2]))
            for col in range(3):
                fromim_t[:,:,col] = ndimage.geometric_transform(fromim[:,:,col],
                                            transf,(toim.shape[0],toim.shape[1]+padding))
        else:
            # pad the destination image with zeros to the left
            toim_t = hstack((zeros((toim.shape[0],padding)),toim))
            fromim_t = ndimage.geometric_transform(fromim,
                                    transf,(toim.shape[0],toim.shape[1]+padding))
    
    # blend and return (put fromim above toim)
    if is_color:
        # all non black pixels
        alpha = ((fromim_t[:,:,0] * fromim_t[:,:,1] * fromim_t[:,:,2] ) > 0)
        for col in range(3):
            toim_t[:,:,col] = fromim_t[:,:,col]*alpha + toim_t[:,:,col]*(1-alpha)
    else:
        alpha = (fromim_t > 0)
        toim_t = fromim_t*alpha + toim_t*(1-alpha)
    
    return toim_t

输出结果：

1.仿射扭曲就是讲图像或者图像的一部分放置在另一幅图像中，使得它们能够和指定的区域或者标记物对齐。在函数image_in_image()中，函数的输入参数是两幅图像和一个坐标。该坐标为将第一幅图像放置到第二幅图像中的角点坐标：

设置仿射映射的目的坐标：

（三）遇到的问题

首先下载一个PCV包，然后进入cmd命令行窗口，进到pcv的路径下，输入：

具体步骤看链接：

http://yongyuan.name/pcvwithpython/installation.html

cd PCV
python setup.py install

出现以上问题就是，你的python版本是python3，里面的warp.py里的删掉matplotlib包里一些方法，里面的matplotlib.delaunay不再被使用了，所以把它换成一个相同功能的就可以，可以在warp.py把import matplotlib.delaunay as md 换成from scipy.spatial import Delaunay，就可以运行。