LCT入门（动态树）（点权）（边权）

LCT的用途：

1，在线链接link&cut（连接边，删除边）

2，查询连通性

3，维护链上信息

4，换根

5，维护子树信息。

等等：

基础知识：

1.伸展树（Splay Tree）

：支持链上求和，求最值，修改，等等操作，

2LCT（link cut tree）：是一棵树，长这样：

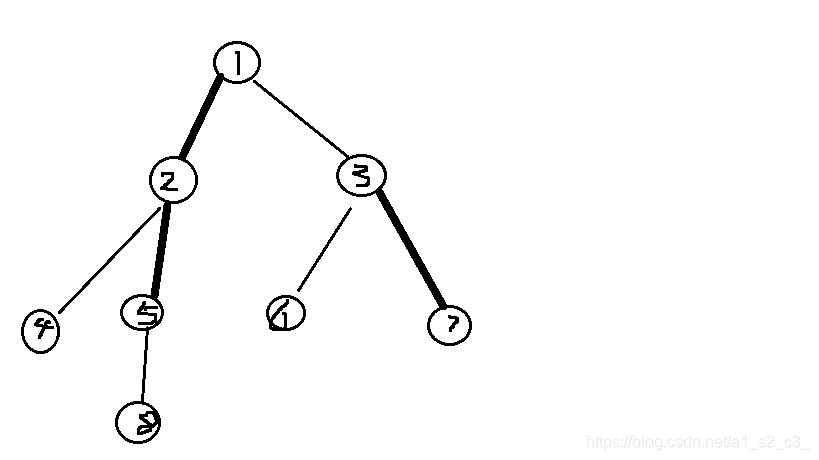
在这里插入图片描述

这上面有一些粗一点的边，我们把它称为

重边

；还有一些细一点的，我们把它称为

轻边

。

基本函数功能介绍：

access（x）

：x-根节点变成重边，专门用一棵splay维护

makeroot(x)

:将x变成整棵LCT树的根。

link(x, y)

:新建一条边，x-y链接起来；

cut(x,y)

:删除边x-y;

split(x,y)

:将x-y路径取出分离。求解u到v的路径上的节点权值和只需

split(u,v)

，然后输出sum[v]即可。

rotate(x)/reverse(x)

:翻转x的子树：

下面来举一个直接套用模板的例子：

在这里插入图片描述

//在上面的代码中除了update（），pushdown()其他的都是模板。

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<cmath>
#include<map>
#include<set>

using namespace std;

inline int read()
{
  int x=0,f=1;char ch=getchar();
  while (!isdigit(ch)) {if (ch=='-') f=-1;ch=getchar();}
  while (isdigit(ch)) {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
  return x*f;
}

const int maxn = 1e6+1e2;

int fa[maxn],ch[maxn][3]; //ch[i][0] -- 代表左孩子，ch[i][1]--代表右孩子； 
int rev[maxn],sum[maxn];    //sum[i]--表示i到根节点的异或和； 
int n,m;
int val[maxn];      //val--代表每一个点的权值。 
int st[maxn];

int son(int x)
{
	if (ch[fa[x]][0]==x) 
	  return 0;
	else return 1;
}

bool notroot(int x)
{
	return (ch[fa[x]][0]==x) || (ch[fa[x]][1]==x);
}

void update(int x)    //这是自己写的，在这个代码中是计算路径权值异或和，配合pushdown（）函数。 
{
	sum[x]=sum[ch[x][0]]^sum[ch[x][1]]^val[x];
}

void reverse(int x)
{
	swap(ch[x][0],ch[x][1]);
	rev[x]^=1;
}
void pushdown(int x)//里面的内容也是自己编辑的。
{
	if (rev[x])
	{
		if (ch[x][0]) reverse(ch[x][0]);
		if (ch[x][1]) reverse(ch[x][1]);
		rev[x]=0;
	}
}

void rotate(int x)
{
	int y=fa[x],z=fa[y];
	int b=son(x),c=son(y);
	if(notroot(y)) ch[z][c]=x;
    fa[x]=z;
	ch[y][b]=ch[x][!b];
	fa[ch[x][!b]]=y;
	ch[x][!b]=y;
	fa[y]=x;
	update(y);
	update(x);
	//cout<<1<<endl;
}

void splay(int x)
{
	int y=x,cnt=0;
	st[++cnt]=y;
	while(notroot(y)){y=fa[y];st[++cnt]=y;}
	while (cnt) pushdown(st[cnt--]);
	while (notroot(x))
	{
		int y=fa[x],z=fa[y];
		int b=son(x),c=son(y);
		if (!notroot(y)) rotate(x);
		else
		//if (notroot(y))
		{
			if (b==c)
			{
				rotate(y);
				rotate(x);
			}
			else
			{
				rotate(x);
				rotate(x);
			}
		}
		//cout<<1<<endl;
	 } 
	 update(x);
}

void access(int x)
{
	for (int y=0;x;y=x,x=fa[x])
	{
		splay(x);
		ch[x][1]=y;
		update(x); 
	}
}

void makeroot(int x)
{
	access(x);
	//splay(x);
	reverse(x);
} 

int findroot(int x)
{
   access(x);
   splay(x);
   while (ch[x][0])
   {
   	  pushdown(x);
   	  x=ch[x][0];
   }
   //splay(x);
   return x;
}

void split(int x,int y)
{
	makeroot(x);
	access(y);
	splay(y);
}

void link(int x,int y)
{
	makeroot(x);
	if (findroot(y)!=x) fa[x]=y;
}

void cut(int x,int y)
{
	split(x,y);
	if (ch[x][0] || ch[x][1] ||fa[x]!=y || ch[y][son(x)^1]) return;
	fa[x]=ch[y][0]=0;
}
//在上面的代码中除了update（），pushdown()其他的都是模板。
int main()
{
   n=read(),m=read();
   for (int i=1;i<=n;i++) val[i]=read();
   for (int i=1;i<=m;i++)
   {
      int opt=read(),x=read(),y=read();
      if(opt==0)  //为0 是计算x-y路径权值异或和。
      {
      	 split(x,y);  //提取这条路径
      	 printf("%d\n",sum[y]);
	  }
	  if(opt==1)//链接两条边
	  {
	  	 link(x,y); 
	  }            //切断两条边
	  if (opt==2)
	  {
	  	cut(x,y);
	  }
	  if (opt==3)
	  {
	  	 splay(x);     //把x转上去再改，不然会影响Splay信息的正确性
	  	 val[x]=y;
	  }
   }
   return 0;
}

第二个例子

在这里插入图片描述

第二个例子在一个例子基础上有所变化：

==求有多少条边经过x-y这一条边；等于：这条边连接的两棵子树大小的乘积 ==

这个中就用不到权值。

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<cmath>
#include<map>
#include<set>

using namespace std;

inline int read()
{
  int x=0,f=1;char ch=getchar();
  while (!isdigit(ch)) {if (ch=='-') f=-1;ch=getchar();}
  while (isdigit(ch)) {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
  return x*f;
}

const int maxn = 1e6+1e2;

int fa[maxn],ch[maxn][3]; //ch[i][0] -- 代表左孩子，ch[i][1]--代表右孩子； 
int rev[maxn],sum[maxn];    //sum[i]--表示i到根节点的异或和； 
int n,m;
int sz[maxn], lit[maxn];    //sz--代表节点子节点个数，lit--代表虚节点个数。 
int val[maxn];      //val--代表每一个点的权值。 
int st[maxn];

int son(int x)
{
	if (ch[fa[x]][0]==x) 
	  return 0;
	else return 1;
}

bool notroot(int x)
{
	return (ch[fa[x]][0]==x) || (ch[fa[x]][1]==x);
}

void update(int x)    //在这个函数中计算每一个点 
{
	//sum[x]=sum[ch[x][0]]^sum[ch[x][1]]^val[x];
	sz[x] = sz[ch[x][0]] + sz[ch[x][1]] + 1 + lit[x];
}

void reverse(int x)
{
	swap(ch[x][0],ch[x][1]);
	rev[x]^=1;
}
void pushdown(int x)
{
	if (rev[x])
	{
		if (ch[x][0]) reverse(ch[x][0]);
		if (ch[x][1]) reverse(ch[x][1]);
		rev[x]=0;
//		if(rev[x])
//		{
//			rev[ch[x][1]] ^= 1;
//			rev[ch[x][0]] ^= 1;
//			rev[x]  = 0;
//			//rev
//			swap[]
//		}
	}
}

void rotate(int x)
{
	int y=fa[x],z=fa[y];
	int b=son(x),c=son(y);
	if(notroot(y)) ch[z][c]=x;
    fa[x]=z;
	ch[y][b]=ch[x][!b];
	fa[ch[x][!b]]=y;
	ch[x][!b]=y;
	fa[y]=x;
	update(y);
	update(x);
	//cout<<1<<endl;
}

void splay(int x)
{
	int y=x,cnt=0;
	st[++cnt]=y;
	while(notroot(y)){y=fa[y];st[++cnt]=y;}
	while (cnt) pushdown(st[cnt--]);
	while (notroot(x))
	{
		int y=fa[x],z=fa[y];
		int b=son(x),c=son(y);
		if (!notroot(y)) rotate(x);
		else
		//if (notroot(y))
		{
			if (b==c)
			{
				rotate(y);
				rotate(x);
			}
			else
			{
				rotate(x);
				rotate(x);
			}
		}
		//cout<<1<<endl;
	 } 
	 update(x);
}
 
void access(int x)    //修改过: 
{
	for (int y=0;x;y=x,x=fa[x])
	{
		splay(x);
		lit[x] += sz[ch[x][1]] - sz[y];  //这个地方； 
		ch[x][1]=y;
		update(x); 
	}
}

void makeroot(int x)
{
	access(x);
	splay(x);
	reverse(x);
} 

int findroot(int x)
{
   access(x);
   splay(x);
   while (ch[x][0])
   {
   	  pushdown(x);
   	  x=ch[x][0];
   }
   //splay(x);
   return x;
}

void split(int x,int y)
{
	makeroot(x);
	access(y);
	splay(y);
}

void link(int x,int y)//修改过：
{
	makeroot(x);
	//if (findroot(y)!=x) fa[x]=y;
	access(y);
	splay(y);
	fa[x] = y;
	lit[y] += sz[x];
	update(y);
}

void cut(int x,int y)
{
	split(x,y);
	if (ch[x][0] || ch[x][1] ||fa[x]!=y || ch[y][son(x)^1]) return;
	fa[x]=ch[y][0]=0;
}

int main()
{
   //n=read(),m=read();
   scanf("%d%d", &n, &m);
   for (int i=1;i<=n;i++) sz[i] = 1;//val[i]=read();
   for (int i=1;i<=m;i++)
   {
   	  char s[10];
   	  int x, y;
      scanf("%s",s);
	  scanf("%d%d",&x,&y);
      if(s[0] == 'Q')
      {
      	makeroot(x);
      	access(y);
      	splay(y);
      	printf("%d\n", sz[x]*(sz[y]-sz[x]));
	  }
	  else
	  {
	  	link(x, y);
	  }
   }
   return 0;
}

上面的两个例子是关于点权的，经过某一条边的，下面这个例子是边权的。

题意：

给定一个边权树，要求支持动态修改边权，询问到某个点最远的点的距离

题目来源：

代码这个算法还不了解，以后补；

代码：

#include <set>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
using namespace std;

typedef long long ll;

int read() {
	char ch;
	for(ch=getchar();ch<'0'||ch>'9';ch=getchar());
	int x=ch-'0';
	for(ch=getchar();ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
	return x;
}

void write(ll x) {
	if (!x) {puts("0");return;}
	char ch[20];int tot=0;
	for(;x;x/=10) ch[++tot]=x%10+'0';
	fd(i,tot,1) putchar(ch[i]);
	puts("");
}

const int N=2e5+5;
const ll inf=1e16;

struct Path{
	int u,v;ll w;
	Path(){}
	Path(int u,int v,ll w):
		u(u),v(v),w(w){}
	Path operator + (const ll x)const{return Path(u,v,w+x);}
	Path operator - (const ll x)const{return Path(u,v,w-x);}
	Path operator + (const Path& x)const{
		Path ret;
		ret.u=u;ret.v=x.u;
		if (ret.u<ret.v) swap(ret.u,ret.v);
		ret.w=w+x.w;
		return ret;
	}
	bool operator < (const Path& x)const{
		if (w!=x.w) return w<x.w;
		if (u!=x.u) return u<x.u;
		return v<x.v;
	}
};

struct Data{
	Path pre,suf,ans;ll sum;
	Data(){}
	Data(Path pre,Path suf,Path ans,ll sum):
		pre(pre),suf(suf),ans(ans),sum(sum){}
	Data operator + (const Data& x)const{
		Data ret;
		ret.pre=max(pre,x.pre+sum);
		ret.suf=max(suf+x.sum,x.suf);
		ret.ans=max(ans,x.ans);
		ret.ans=max(ret.ans,suf+x.pre);
		ret.sum=sum+x.sum;
		return ret;
	}
};

namespace LCT{
	int f[N],t[N][2],p[N],sta[N],top;
	multiset<Path> pre[N],ans[N];
	ll val[N];
	Data a[N],ra[N],dp[N];
	bool rev[N];

	void upd(int x) {
		int ls=t[x][0],rs=t[x][1];
		a[x]=ra[x]=Data(dp[x].pre+val[x],dp[x].pre+val[x],dp[x].ans,val[x]);
		if (ls) {
			a[x]=a[ls]+a[x];
			ra[x]=ra[x]+ra[ls];
		}
		if (rs) {
			a[x]=a[x]+a[rs];
			ra[x]=ra[rs]+ra[x];
		}
	}

	int son(int x) {return t[f[x]][1]==x;}

	void rotate(int x) {
		int y=f[x],z=son(x);
		if (f[y]) t[f[y]][son(y)]=x;
		else p[x]=p[y],p[y]=0;
		if (t[x][1-z]) f[t[x][1-z]]=y;
		t[y][z]=t[x][1-z];t[x][1-z]=y;
		f[x]=f[y];f[y]=x;
		upd(y);upd(x);
	}

	void reverse(int x) {
		if (!x) return;
		swap(t[x][0],t[x][1]);
		swap(a[x],ra[x]);
		rev[x]^=1;
	}

	void down(int x) {
		if (rev[x]) {
			reverse(t[x][0]);reverse(t[x][1]);
			rev[x]=0;
		}
	}

	void remove(int x,int y) {
		do {sta[++top]=x;x=f[x];} while (x!=y);
		for(;top;down(sta[top--]));
	}

	void splay(int x,int y) {
		remove(x,y);
		while (f[x]!=y) {
			if (f[f[x]]!=y) 
				if (son(x)==son(f[x])) rotate(f[x]);
				else rotate(x);
			rotate(x);
		}
	}

	void get(int x) {
		dp[x].pre=*pre[x].rbegin();
		dp[x].ans=*ans[x].rbegin();
		if (pre[x].size()>=2) {
			auto smx=pre[x].rbegin(),mx=smx;smx++;
			dp[x].ans=max(dp[x].ans,*smx+*mx+val[x]);
		}
	}

	void add(int x,int y) {
		pre[x].insert(a[y].pre);
		ans[x].insert(a[y].ans);
		get(x);
	}

	void del(int x,int y) {
		pre[x].erase(pre[x].find(a[y].pre));
		ans[x].erase(ans[x].find(a[y].ans));
		get(x);
	}

	void access(int x) {
		int y=0;
		for(;x;y=x,x=p[x]) {
			splay(x,0);
			if (t[x][1]) {
				add(x,t[x][1]);
				f[t[x][1]]=0;p[t[x][1]]=x;
			}
			if (y) {
				del(x,y);
				f[y]=x;p[y]=0;
			}
			t[x][1]=y;
			upd(x);
		}
	}

	void make_root(int x) {access(x);splay(x,0);reverse(x);}

	void link(int u,int v) {
		make_root(u);make_root(v);
		p[v]=u;add(u,v);upd(u);
	}

	bool check(int u,int v) {
		make_root(u);access(v);
		splay(v,0);
		for(;u&&u!=v;u=f[u]);
		return u==v;
	}
}

int n;
char opt[5];

int main() {
	n=read();
	fo(i,1,n) {
		LCT::pre[i].insert(Path(i,i,0));
		LCT::ans[i].insert(Path(i,i,0));
		LCT::get(i);LCT::upd(i);
	}
	fo(i,1,n-1) {
		int x=read(),y=read(),z=read(),v=i+n;
		LCT::val[v]=z;
		LCT::pre[v].insert(Path(0,0,-inf));
		LCT::ans[v].insert(Path(0,0,-inf));
		LCT::get(v);LCT::upd(v);
		if (LCT::check(x,y)) continue;
		LCT::link(x,v);LCT::link(v,y);
	}
	for(int q=read();q;q--) {
		scanf("%s",opt);
		if (opt[0]=='C') {
			int x=read()+n,y=read();
			LCT::make_root(x);LCT::access(x);
			LCT::val[x]=y;LCT::get(x);LCT::upd(x);
		}
		if (opt[0]=='Q') {
			int x=read();
			LCT::make_root(x);
			write(LCT::a[x].pre.w);
		}
	}
	return 0;
}

原文链接：https://blog.csdn.net/a1_s2_c3_/article/details/101199124

基本函数功能介绍：

上面的两个例子是关于点权的，经过某一条边的，下面这个例子是边权的。

你可能也喜欢