0 笔记说明
本博文是对2021年李永乐老师线代基础课的重点笔记的二次整理。根据李老师使用的教材即同济版《工程数学:线性代数》第五版的目录,我将自己的笔记分为6大节,我会尽量将每条笔记放在合适的章节。如果遇到复杂公式,由于未学习LaTeX,我会上传手写图片或教材公式截图等代替(手机相机可能会拍的不太清楚,但是我会尽可能使内容完整可见)。
本笔记不是对上述教材的系统性整理,只适用于自己以后的学习与研究。
1 行列式
没什么特别要记的公式。
2 矩阵及其运算
1、求A
-1
B:构造矩阵(A|B),通过初等变换化为(E|X),X即为所求。
2、求AB
-1
:构造矩阵(B
T
|A
T
),通过初等变换化为(E|X),X
T
即为所求。
3、若A是n阶矩阵,则① r(A)<k⇔A的k阶子式(如果有)全为0;② r(A)≥k⇔A的k阶子式中存在不为0的;③A≠0⇔r(A)≥1;④r(A)=n⇔|A|≠0⇔A是可逆矩阵;⑤r(A)<n⇔|A|=0⇔A不可逆;
4、A、B是n阶矩阵,若A可逆,则r(AB)=r(B),r(BA)=r(B)。
5、A、B是n阶矩阵,max{r(A),r(B)}≤r(A|B)≤r(A)+r(B)。
6、设A
*
是n阶矩阵A的伴随矩阵,则有:① |A
*
|=|A|
n-1
;② A
-1
=A
*
/|A|;③AA
*
=|A|E;④|kA|=k
n
|A|。
7、A和B是m×n阶矩阵,若存在n阶可逆矩阵P,m阶可逆矩阵Q,使得B=QAP,则称A与B等价,记作A≌B。
8、A和B是m×n阶矩阵,则A≌B⇔r(A)=r(B)⇔A经过有限次的初等变换可以得到B。
9、设A
*
是n阶矩阵A的伴随矩阵,有:① 若r(A)=n,则r(A
*
)=n;② 若r(A)=n-1,则r(A
*
)=1;③ 若r(A)≤n-2,则r(A
*
)=0。
10、r(A
T
A)=r(A)=r(A
T
)=r(AA
T
)。
3 矩阵初等变换与线性方程组
1、对于n元线性方程组Ax=b,有:① 无解⇔r(A)+1=r(A|b);② 唯一解⇔r(A)=r(A|b)=n;③ 无穷多解⇔r(A)=r(A|b)<n。
2、对于n元齐次线性方程组Ax=0,有:① 有非零解⇔r(A)<n;② 只有零解⇔r(A)=n。
3、矩阵方程AX=B有解⇔r(A)=r(A|B)。
4、若方程组中方程的个数少于未知数的个数,则方程组必有非零解。
5、A经过有限次的初等行变换得到B,则A≌B,且一定存在可逆矩阵P,使得PA=B。A与B的列向量:① 有相同的线性相关性;② 有相同的线性表示法。
4 向量组的线性相关性
1、<α,β>为向量α与β的向量积运算,则<α,β>
2
=||α||
2
·||β||
2
,等号当且仅当α与β线性相关时成立。
2、三维向量空间中,设向量α与β在同一组基下的坐标分别为(a
1
,a
2
,a
3
)与(b
1
,b
2
,b
3
),设α与β之间夹角为θ,则:
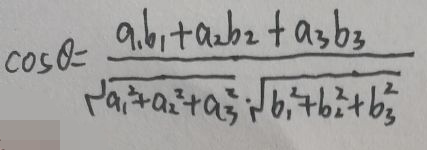
3、设n维向量α
1
,α
2
,…,α
n
是一组两两正交的非零向量组,则α
1
,α
2
,…,α
n
是线性无关向量组。
4、向量组Ⅰ等价于向量组Ⅱ的充要条件是向量组Ⅰ于向量组Ⅱ可互相线性表出。
5、若向量组Ⅰ可由向量组Ⅱ线性表出,则r(向量组Ⅰ)≤r(向量组Ⅱ);若向量组Ⅰ可由向量组Ⅱ线性表出,且向量组Ⅰ的向量个数>向量组Ⅱ的向量个数,则向量组Ⅰ必线性相关;若向量组Ⅰ线性无关,且向量组Ⅰ可由向量组Ⅱ线性表出,则向量组Ⅰ的向量个数≤向量组Ⅱ的向量个数。
6、向量组Ⅰ等价于向量组Ⅱ⇔r(向量组Ⅰ)=r(向量组Ⅱ)=r(向量组Ⅰ,向量组Ⅱ)。
7、n+1个n维向量必线性相关;若向量组α
1
,α
2
,…,α
s
线性相关,则α
1
,α
2
,…,α
s
,…,α
t
必线性相关;若向量组Ⅰ无关,则扩充向量组Ⅰ中每个向量的维数后的高维向量组依然无关。
8、单个向量α
1
相关⇔α
1
是零向量;两个向量α
1
,α
2
相关⇔α
1
,α
2
共线;三个向量α
1
,α
2
,α
3
相关⇔α
1
,α
2
,α
3
共面。
9、若向量组Ⅰ内的向量均为单位向量,即每个向量的模长均为1,且向量之间两两正交,即内积为0,则称向量组Ⅰ为标准正交组。
5 相似矩阵及二次型
1、设A是n阶矩阵,α是n维非零列向量,若有A·α=λ·α,则称λ是矩阵A的特征值,α是矩阵A对应于特征值λ的特征向量。
2、设A是n阶矩阵,则① A的迹tr(A)=Σλ
i
=Σa
ii
;② Πλ
i
=|A|。这样,A可逆⇔A的特征值均非零。
3、矩阵A的不同特征值的特征向量之间是线性无关的。若A为n阶实对称矩阵,则A的不同特征值的特征向量之间是两两正交的。
4、设A与B均是n阶矩阵,若存在可逆矩阵P使得P
-1
AP=B,则A~B。
5、若A~B,则① |λE-A|=|λE-B|,且A与B的特征值完全相同;② r(A)=r(B);③ |A|=|B|;④ tr(A)=tr(B)。
6、若3阶矩阵A可以相似对角化为矩阵Λ,则A的特征值λ
1
、λ
2
、λ
3
构成对角矩阵Λ=diag(λ
1
,λ
2
,λ
3
),A的对应于λ
1
、λ
2
、λ
3
的特征向量r
1
、r
2
、r
3
构成可逆矩阵P=(r
1
,r
2
,r
3
),有P
-1
AP=Λ,即A~Λ。
7、若三阶矩阵A有3个无关的特征向量r
1
、r
2
、r
3
,满足A·r
i
=λ
i
·r
i
,i=1,2,3。即A(r
1
,r
2
,r
3
)=(λ
1
·r
1
,λ
2
·r
2
,λ
3
·r
3
)=(r
1
,r
2
,r
3
)·diag(λ
1
,λ
2
,λ
3
),令P=(r
1
,r
2
,r
3
),Λ=diag(λ
1
,λ
2
,λ
3
),则AP=PΛ,即P
-1
AP=Λ。总之,n阶矩阵A可以相似对角化⇔A有n个无关的特征向量。
8、若n阶矩阵A有n个不同的特征值,则A一定可以相似对角化;若λ是A的k重特征值,则λ至多对应k个无关的特征向量;A可以相似对角化⇔若λ是矩阵A的k重特征值,则λ对应k个无关的特征向量。
9、若A为n阶实对称矩阵,则A的特征值均为实数。
10、A为任意一个n阶实对称矩阵,则一定存在n阶正交矩阵P,使得P
-1
AP=Λ=diag(λ
1
,λ
2
,…,λ
n
)。
11、二次型及其矩阵表示如下,矩阵A的秩就是二次型的秩:
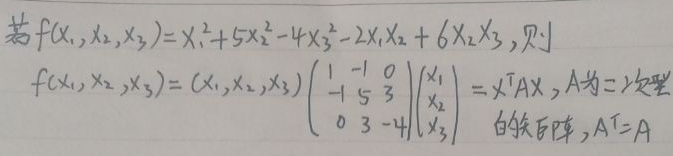
12、二次型的标准型只有平方项,没有混合项:

13、二次型的规范型首先必须是标准型,即只有平方项,没有混合项,其次平方项的系数只能是-1,0,+1,如:
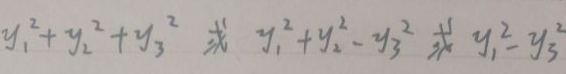
14、针对标准型,记正惯性指数为p,副惯性指数为q。如针对上图的三个二次型,分别为【p=3,q=0】、【p=2,q=1】、【p=1,q=1】。
15、二次型的变换:

16、合同:若C
T
AC=B,其中C可逆,则称A与B合同,记为A≃B。
17、任意一个二次型均可通过坐标变换化为标准型,有两个方法——配方法与正交变换法。
18、对任意一个二次型f=x
T
Ax,其中A
T
=A,总存在正交变换x=Py,其中P为正交矩阵,使得二次型化为标准型x
T
Ax=y
T
Λy=Σλ
i
·y
i
2
,其中λ
i
为A的n个特征值。
19、二次型的规范型是唯一的(惯性定理):对任意一个二次型x
T
Ax,经过坐标变换后化为的标准型中,正负惯性指数是唯一确定的。
20、正定二次型:设二次型f(x)=x
T
Ax,若对任意非零向量x=(x
1
,x
2
,…,x
n
)
T
,恒有f(x)>0,则称f(x)为正定二次型,相应的矩阵A称为正定矩阵。
21、二次型经过坐标变换不改变其正定性:在坐标变换x=Cy下,二次型x
T
Ax与二次型y
T
C
T
ACy的正定性相同。
22、二次型正定的必要条件是所有主对角元素a
ii
>0。二次型正定的充要条件:① 二次型f(x)=x
T
Ax正定;② f(x)的标准型的平方项系数均大于0;③ 正惯性指数p=n;④ A与E合同,即存在可逆C,使得C
T
AC=E,A≃E;⑤ A的特征值均大于0;⑥ A的顺序主子式均大于0。
23、n阶实对称矩阵A正定的必要条件是|A|>0。n阶实对称矩阵A正定的充要条件:① A与E合同,即存在可逆C,使得C
T
AC=E,A≃E;② A的正惯性指数等于n;③ A的顺序主子式均大于0;④ A的特征值均大于0;⑤ 存在可逆U,使得A=U
T
U。
24、相似矩阵有相同的特征值、特征多项式、行列式、秩、迹。
25、若A是n阶矩阵,设A的r个互不相同的特征值为λ
1
,λ
2
,…,λ
r
,且对应的重根数分别为p
1
,p
2
,…,p
r
,则称p
i
是λ
i
的代数重复度,λ
i
对应的特征空间的维数即λ
i
的无关的特征向量个数称为几何重复度。
26、λ矩阵与数字矩阵的逆(如果可逆)均为:A
-1
=A
*
/|A|。
27、任意λ矩阵可逆的充要条件是其行列式是非零常数。
28、设λ矩阵A(λ)的秩为r:① 行列式因子:对于正整数1≤k≤r,A(λ)必有非零的k阶子式,A(λ)的全部非零的k阶子式的首项系数为1的最大公因式D
k
(λ)称为A(λ)的k阶行列式因子;② A(λ)的不变因子:
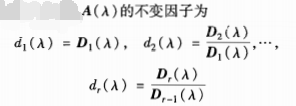
若n阶λ矩阵A(λ)满秩,则c·Πd
i
(λ)=|A(λ)|,c为非零常数,所有d
i
(λ)的次数之和=n;③ 初等因子可由不变因子中不是1的不变因子拆项得到,下面是一个例子:

29、设A与B均是n阶数字矩阵,则A~B的充要条件为:① λE-A≌λE-B;② λE-A与λE-B有相同的施密特标准型;③ λE-A与λE-B有相同的不变因子;④ λE-A与λE-B有相同的行列式因子;⑤ λE-A与λE-B有相同的初等因子。
30、对于数字矩阵A,称λE-A的不变因子就是A的不变因子,同时称λE-A的初等因子就是A的初等因子。
31、若A是n阶矩阵,设λE-A的秩为r,λE-A的不变因子为d
i
(λ),i=1…r。则λE-A的施密特标准型为:

6 线性空间与线性变换
1、向量组(α
1
,α
2
,α
3
)与(β
1
,β
2
,β
3
)是三维向量空间不同的两个基,若(β
1
,β
2
,β
3
)=(α
1
,α
2
,α
3
)·P,则称P为向量组(α
1
,α
2
,α
3
)到(β
1
,β
2
,β
3
)的过渡矩阵。P=(β
1
,β
2
,β
3
)
-1
·(α
1
,α
2
,α
3
)。
2、同一线性变换在不同基下的矩阵是相似的,相似矩阵有相同的特征值、特征多项式、行列式、秩、迹。
3、设V
1
、V
2
是线性空间V的两个子空间,若V
1
∩V
2
={0向量},则称V
1
与V
2
的和空间V
1
+V
2
是直和,记作V
1
⊕V
2
。下面命题是等价的:① V
1
+V
2
是直和;② dim(V
1
+V
2
)=dim(V
1
)+dim(V
2
);③ 若向量组Ⅰ是V
1
的一个基,向量组Ⅱ是V
2
的一个基,则{向量组Ⅰ,向量组Ⅱ}是V
1
+V
2
的一个基。
4、设W是V的子空间,取α∈V,若对任意β∈W,都有α⊥β,则称α⊥W。
5、勾股定理:若α与β均为非零向量,且α⊥β,则有||α+β||=||α-β||=||α||
2
+||β||
2
。
最后数了一下才知道正好是60条笔记,哈哈!
END