目录
目录
CH1 简介
1. Simutaneous localization and Mapping 解决定位与建图的问题,为路径规划做准备
2.
应用1:定位
弥补民用GPS精度的不足,室内无GPS,救援,反恐。
扫地机器人
AGV(Automated Guided Vehicle)
应用2:建图
VR、游戏、三位全景漫游
算法框架

分为激光slam和视觉slam


知识树

发展趋势
1. 消费级3D相机的广泛应用,无人驾驶技术的发展
2. 视觉slam越来越重要
3. 多传感器融合是大方向
4. 有适合的刚需场景
5. 入门难,人才缺口越来越大
6. 可替代性不强
CH2
时间:2021.6.6
1. 结构:场景的远近和大小
2. 单目相机有尺度不确定性:没办法确定二维图像的绝对大小。因此,需要双目相机和深度相机
3. 双目相机测定距离是通过对比左右眼图像实现的。
其缺点是:需要的计算资源大
4. RGB-D相机:有点像激光
缺点:测量范围债、容易受日光影响(因此主要用于室内)。
5. SLAM 框架(图是自己画的,可能丑了点)

6. SLAM的数学表示

其中第一个方程为
位置方程
:
Xk表示
位姿
,Uk表示运动传感器的读入,Wk是该过程加入的噪声;
是第二个方程为
观测方程
:Zk表示观测数据,Xk是位置,Vk是观测里的噪声
这个方程在
二维
的具体化为:


x1、x2确定位置,θ为转角(姿态),三个确定位姿
r为小萝卜于一个路标的距离(对应度量地图),Φ为夹角
CH2~2
时间:2021.6.11
今天主要学习了在Ubuntu18.04的环境下编程
1. 在一开始,我连创建一个文本文档都不会,还是在网上查了之后才知道要用gedit;
2. g++作为编译器,可以来编辑文件:在创建了helloslam.cpp之后,可以用在teminal 运行g++ helloslam.cpp来生成可执行文件。
3. 而cmake可以使链接等事情更加方便,通过创建一个CMakeLists.txt来实现此功能
先创建Helloslam.cpp、libHelloslam.cpp、libHelloslam.h
//在CMakeLists.txt中
project(Helloslam) //声明文件
add_exectable(Helloslam Helloslam.cpp) //添加源文件(可执行)
add_library(hello libHelloslam.cpp) //添加库文件,
add_library(hello_shared SHARED libHelloslam.cpp) 生成共享库
target_link_libraries(Helloslam hello_shared) //使Helloslam可执行文件和hello_shared共性库链接起来(前提是Helloslam里有include “libHelloslam.h”,libHelloslam.cpp对应的声明)
然后:创建一个build来储存中间文件
//teminal里
cd build
cmake ..
make
./Helloslam
即可执行
3. 在Kdevelop这个IDE里,可以直接省略teminal里的东西
值得注意的是,在里面CMakeLists.txt要添加set(CMAKE_BUILD_TYPE “Debug”),然后去run那里添加一个启动器;
还有一个搞我心态的一点:修改之后一定要点击左上角的build,才能执行不然会显示没有修改。
CH3
时间:2021.6.19
此次内容的学习大多于线代挂钩,如坐标变换(正交变换),旋转矩阵(正交阵的一个特殊例子)
1. 外积
(叉乘)可以用矩阵a^b来表示,其中a^表示该矩阵为反对称矩阵(A的转置=负A)aXb=a^b a^=
2. 欧氏变换
:(坐标变换)
前面为坐标系1,后面为坐标系2

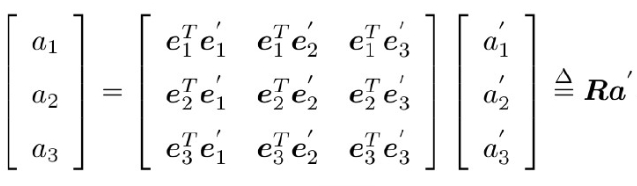
表示坐标系2
旋转变化
到坐标系1,R称为旋转矩阵(列向量两两正交,|A|=+1)
若是加上平移
其中:
表示从2坐标系变化到1坐标系,
表示坐标系1原点坐标指向坐标系2原点坐标的向量(指向被减向量)
3. 因为不是线性变化(有一个t)所以把非线性问题转化为线性问题

这样太麻烦,转化为

注意,此时三维问题用四维表示
T称为
变换矩阵
CH3~Eigen库的学习
1.eigen库的链接:
首先,按下快捷键
Ctrl + Shift + P
,输入
edit configuration
,选择
C/Cpp: Edit Configurations...
,此时会在工程的配置目录
.vscode
下生成一个配置文件:
c_cpp_properties.json,
(注:json文件中是不能添加注释在里面的),添加一行:”/usr/include/eigen3” 在includePath里面,如下
"includePath": [
"${workspaceFolder}/**",
"/usr/include/eigen3"
],Eigen 库的路径要写成#include 的形式,写#include 的形式可能vscode识别不出来
2. 定义方式
方式1:在开头添加一个模板:
template
using Mat2 = Matrix;
以后Mat2相当于一个像int类型的关键字,申明的都是2X2的矩阵
方式2:Vector2d vec;
定义了一个2维向量,2d可以变成3d,就是三维向量
方式3:直接用Matrixmat;(推荐)
这种方式是比较推荐的的方式
方式4:用MatrixXd mat(m,n);(推荐)
与上面区别不大,默认为double类型
3. 输入数据
mat<
实际上这个<<是在eigen库里进行了重载的。
特殊矩阵的输入:
MatrixXd zero=MatrixXd::Zero(3,2); //纯0阵
MatrixXd one=MatrixXd::Ones(3,3); //纯1阵
MatrixXd E=MatrixXd::Identity(4,4); //单位阵
MatrixXd rand=MatrixXd::Random(5,2); //随机阵,值-1到1
#include <iostream>
#include <eigen3/Eigen/Dense>
using namespace std;
using namespace Eigen; //
template <typename T>
using Mat2 = Matrix<T,2,2>;//Mat2定义成2X2的矩阵
int main(void)
{
#if 0
Mat2<int> mat1; //自定的定义方式
mat1<<6,1, //重载的<<
1,3;
cout<<mat1<<endl<<endl;
Vector2d vec1; //eigen自带的定义方式1
vec1<<1,2;
cout<<vec1<<endl<<endl;
Matrix< double, 2, 3 > matrix_NN;//方式2:定义一个2X3的double矩阵
MatrixXd mat(2,2); //更常用的方法
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
mat(i,j)=2;
//也可以使用mat<<2,2,2,2;
cout<<mat<<endl<<endl;
//常见的矩阵
MatrixXd zero=MatrixXd::Zero(3,2); //纯0阵
MatrixXd one=MatrixXd::Ones(3,3); //纯1阵
MatrixXd E=MatrixXd::Identity(4,4); //单位阵
MatrixXd rand=MatrixXd::Random(5,2); //随机阵,值-1到1
cout<<zero<<endl<<endl<<one<<endl<<endl<<E
<<endl<<endl<<rand<<endl;
#endif
MatrixXd mat2=MatrixXd::Ones(2,2); //若是不赋值,则直接打印出来为纯0阵
cout<<mat2<<endl<<endl<<mat2.rows()<<' '<<mat2.cols()<<endl;
MatrixXd mat3(3,3);
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
mat3(i,j)=2;
mat2=mat3; //强制转换会使其变为等号后的长宽
//这个变成3X3,前2X2是mat3的2X2,其他变为0
//2 2 0
//2 2 0
//0 0 0
cout<<mat2<<endl<<endl<<mat2.rows()<<' '<<mat2.cols()<<endl;
return 0;
}
4. 矩阵基本运算
1)加减乘照样,应该也是经过了运算符重载
2)逆、转置、行列式等:
cout<<"transpose"<<endl<<mat2.transpose()<<endl; //转置矩阵
cout<<"inverse"<<endl<<mat2.inverse()<<endl; //逆矩阵
cout<<"adjoint"<<endl<<mat2.adjoint()<<endl; //伴随矩阵
cout<<"conjugate"<<endl<<mat2.conjugate()<<endl; //共轭矩阵
cout<<"各元素数和"<<endl<<mat2.sum()<<endl; //数和
cout<<"行列式"<<endl<<mat2.determinant()<<endl; //行列式
cout<<"迹"<<endl<<mat2.trace()<<endl; //迹
mat2.setZero(); //清03) 求特征值、特征向量:
eigen_solver.eigenvalues();
eigen_solver.eigenvectors();
4)矩阵分块操作
a.向量分块:
vec.head(n);
vec.tail(n);
vec.block(m,n);
b.矩阵分块
mat.block(1,0,2,4); //以(1,0)位置的点为标准,向下取2行,向右取4列
或者:
mat.block<2,4>(1,0);
#include <iostream> //块操作
#include <eigen3/Eigen/Dense>
using namespace std;
using namespace Eigen;
int main(void)
{
MatrixXd mat1(9,1);
mat1<<1,2,3,4,5,6,7,8,9;
cout<<"mat1"<<endl<<mat1<<endl;
ArrayXd vec(9);
vec<<1,2,3,4,5,6,7,8,9;
cout<<"head:"<<endl<<vec.head(3)<<endl;//前3个
cout<<"tail:"<<endl<<vec.tail(3)<<endl;//后三个
cout<<"segment"<<endl<<vec.segment(3,6)<<endl; //4到7的元素
MatrixXd mat=MatrixXd::Identity(4,4);
cout<<mat.row(3)<<endl; //第4行
cout<<mat.col(1)<<endl; //第2列
cout<<mat.block(1,0,2,4)<<endl<<endl; //以(1,0)位置的点为标准,向下取2行,向右取4列
cout<<mat.block<2,4>(1,0)<<endl; //同上
return 0;
}
CH3~各种旋转的表示方式
time:2021.7.13
一. 旋转向量
def:任意一个旋转可以用一个旋转向量表示,该向量的方向与旋转轴一致,长度为
,表示为
旋转向量与旋转矩阵的转换:
R=Icosθ+(1-cosθ)n*
n
T+n^sinθ
二. 欧拉角
def:把一个旋转分解为3次绕不同方向的旋转

以ZYX为例(绕旋转之后的轴)



不足:存在万向锁问题,即若绕y轴的旋转为
时(
第二次旋转
),第一次旋转和第三次旋转的轴相同,失去了一个自由度。也称奇异性。
三. 四元数
def:
任意
单位四元数
可以表示一个旋转,若四元数不是单位四元数,要进行归一化。
1.虚部的含义
i,j,k之间有以下关系
i2 = j2 = k2 = -1
ij = k,ji =-k
jk = i, kj = -i
ki= j, ik = -j
乘以i对应着旋转180° , 而
意味着绕i轴旋转360° 后得到一个相反的东西。 这个东西要旋转两周才会和它原先的样子相等。
2.运算规则
1. 加减

2. 乘




6. 数乘

3. 与其他表示旋转的量的转换
1)四元数到旋转矩阵
首先引入:e

易证:
![]()
设p’和p都是虚四元数(用来表示位置)
所以:


2)四元数到旋转向量

四. eigen库的实战
(和十四讲里的不同,是自己做完再试一次的)
1. 自制思维导图

2. 代码
#include <iostream>
#include <eigen3/Eigen/Geometry>
#include <eigen3/Eigen/Core>
#include <cmath>
using namespace std;
using namespace Eigen;
/*
旋转:
旋转向量
旋转矩阵
欧拉角
四元数
变换:
欧氏变换矩阵
*/
int main(void)
{
Vector3d vec(0,0,1);
//表示旋转的几种方法的转换
//旋转向量向旋转矩阵
AngleAxisd rovector(M_PI/3,Vector3d(1,0,0));
Matrix3d romatrix=rovector.matrix();
cout<<"旋转矩阵="<<endl<<romatrix<<endl;
cout<<"旋转之后="<<endl<<rovector*vec<<endl<<endl;
cout<<"旋转之后="<<endl<<romatrix*vec<<endl<<endl;
//旋转矩阵向欧拉角
Vector3d euleranger = romatrix.eulerAngles(0,1,2);
cout<<"欧拉角"<<endl<<euleranger.transpose()<<endl<<endl;
//旋转向量向四元数
Quaterniond q (rovector);
cout<<"四元数="<<endl<<q.coeffs()<<endl; //coeffs(q1,q2,q3,q0)
cout<<"旋转之后="<<endl<<q*vec<<endl<<endl;
//旋转矩阵向四元数
Quaterniond q1 (romatrix);
cout<<"四元数="<<endl<<q1.coeffs()<<endl;
cout<<"旋转之后="<<endl<<q1*vec<<endl<<endl;
//表示转换:平移加旋转,欧氏变换矩阵
Vector3d tranvector (0,1,0); //平移参数
Isometry3d isomatrix=Isometry3d::Identity(); //初始化
isomatrix.rotate(rovector); //旋转部分赋值(R)
isomatrix.pretranslate(tranvector); //平移部分赋值(t)
cout<<"欧氏变换矩阵="<<endl<<isomatrix.matrix()<<endl;
/*
R t
0 1
实际数据:
1 0 0 0
0 0.5 -0.866025 1
0 0.866025 0.5 0
0 0 0 1
*/
cout<<"变换之前="<<endl<<vec<<endl<<endl;
cout<<"旋转之后="<<endl<<romatrix*vec<<endl<<endl;
cout<<"变换之后="<<endl<<isomatrix*vec<<endl<<endl;
}
CH3~pangolin库的初级使用
时间:7月16日
单开这个节来说是要对自己的态度进行深刻的反思。我这一步从7月14就开始了,但当天尝试了很多次没有成功,就有点挫败,打算7月15再开始重新尝试。但7月15当天可能还是逃离挫败心理,没有立即开始尝试,而是想着早上先看番剧,下午再学。就这样,我一天看了一部24集的番剧,一点都没有学习。然后今天开始再次尝试,居然半个小时就搞定了,我突然有点怀疑我之前在害怕什么了。无非是按照教程一步步来,不过,我还是 没有习惯用cmake,太麻烦了,所以现在开始 要习惯在vscode下开始用cmake。
下面是成果图:


CH3~课后习题:
1~3,6题:
https://zhuanlan.zhihu.com/p/369180479
4:

5:
#include <iostream>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main(void)
{
MatrixXd origin_matrix=MatrixXd::Random(5,5);
cout<<"origin matrix is"<<endl<<origin_matrix<<endl;
Matrix3d sub_matrix=origin_matrix.block(0,0,3,3);
cout<<"sub matrix is"<<endl<<sub_matrix<<endl;
sub_matrix=MatrixXd::Identity(3,3);
cout<<"now sub matrix is"<<endl<<sub_matrix<<endl;
}
补:review
1.
不同
类型
的矩阵不能进行运算;如double类型不能和float类型进行运算,Eigen库里自定义的都 是double类型的。如下,matrix_23是double,v_3d是float,这么解决:
Eigen::Matrix<double,2,1> result=matrix_23.cast<double>()*v_3d;
2.
计算特征向量必须保证方阵是
SelfAdjointEigenSolver<Matrix3d> eigen_solver(matrix_33);
其中直接Matrix<double,3,3>只能计算特征值,而上面都可以。
3.
对Matrix_33*x=v_Nd;
QR分解:x=Matrix_33.colPivHouseholderQr().solve(v_Nd);
cholesky分解:x=Matrix_33.Idlt().solve(v_Nd);
4.
旋转向量中的n为单位向量。
5.
Rn=n;
6.
任意单位四元数描述一个旋转
pangolin的学习
要包含unistd.h
#include <pangolin/pangolin.h>
#include <Eigen/Core>
#include <unistd.h>
// 本例演示了如何画出一个预先存储的轨迹
using namespace std;
using namespace Eigen;
// path to trajectory file
string trajectory_file = "./trajectory.txt";
void DrawTrajectory(vector<Isometry3d, Eigen::aligned_allocator<Isometry3d>>);
int main(int argc, char **argv) {
vector<Isometry3d, Eigen::aligned_allocator<Isometry3d>> poses;
ifstream fin(trajectory_file);
if (!fin) {
cout << "cannot find trajectory file at " << trajectory_file << endl;
return 1;
}
while (!fin.eof()) {
double time, tx, ty, tz, qx, qy, qz, qw;
fin >> time >> tx >> ty >> tz >> qx >> qy >> qz >> qw;
Isometry3d Twr(Quaterniond(qw, qx, qy, qz));
Twr.pretranslate(Vector3d(tx, ty, tz));
poses.push_back(Twr);
}
cout << "read total " << poses.size() << " pose entries" << endl;
// draw trajectory in pangolin
DrawTrajectory(poses);
return 0;
}
/*******************************************************************************************/
void DrawTrajectory(vector<Isometry3d, Eigen::aligned_allocator<Isometry3d>> poses) {
//创建窗口,(窗口名字,长,宽)
pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 1000);
glEnable(GL_DEPTH_TEST);//深度测试
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
pangolin::OpenGlRenderState s_cam(
pangolin::ProjectionMatrix(1024, 1000, 420, 420, 320, 240, 0.1, 1000),//(h,w,fx,fy,cx,cy,最近距离,最远距离)
pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0) //
);
pangolin::View &d_cam = pangolin::CreateDisplay()
.SetBounds(0.0, 1.0, 0.0, 1.0, -1024.0f / 1000.0f)//边界(左,右,上,下,长宽比),0表示碰到边界
.SetHandler(new pangolin::Handler3D(s_cam)); //新建一个相机
while (pangolin::ShouldQuit() == false) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);//清空颜色和深度缓存,刷新显示
d_cam.Activate(s_cam);//激活显示并设置状态矩阵
glClearColor(1.0f, 1.0f, 1.0f, 1.0f);//使用红,绿,蓝以及AFA值来清除颜色缓冲区的,并且都被归一化在(0,1)之间的值,其实就是清空当前的所有颜色
glLineWidth(2);
for (size_t i = 0; i < poses.size(); i++) {
// 画每个位姿的三个坐标轴
Vector3d Ow = poses[i].translation();
Vector3d Xw = poses[i] * (0.1 * Vector3d(1, 0, 0));
Vector3d Yw = poses[i] * (0.1 * Vector3d(0, 1, 0));
Vector3d Zw = poses[i] * (0.1 * Vector3d(0, 0, 1));
glBegin(GL_LINES);//开始
glColor3f(1.0, 0.0, 0.0);//x轴用red
glVertex3d(Ow[0], Ow[1], Ow[2]);
glVertex3d(Xw[0], Xw[1], Xw[2]);
glColor3f(0.0, 1.0, 0.0);//y轴用green
glVertex3d(Ow[0], Ow[1], Ow[2]);
glVertex3d(Yw[0], Yw[1], Yw[2]);
glColor3f(0.0, 0.0, 1.0);//z轴用blue
glVertex3d(Ow[0], Ow[1], Ow[2]);
glVertex3d(Zw[0], Zw[1], Zw[2]);
glEnd();//结束
}
// 画出连线
for (size_t i = 0; i < poses.size(); i++) {
glColor3f(0.0, 0.0, 0.0);
glBegin(GL_LINES);
auto p1 = poses[i], p2 = poses[i + 1];
glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
glEnd();
}
pangolin::FinishFrame();
usleep(5000); // sleep 5 ms
}
}

自己改了一点代码
该了y轴和连线的颜色,顺便改了窗口长宽比
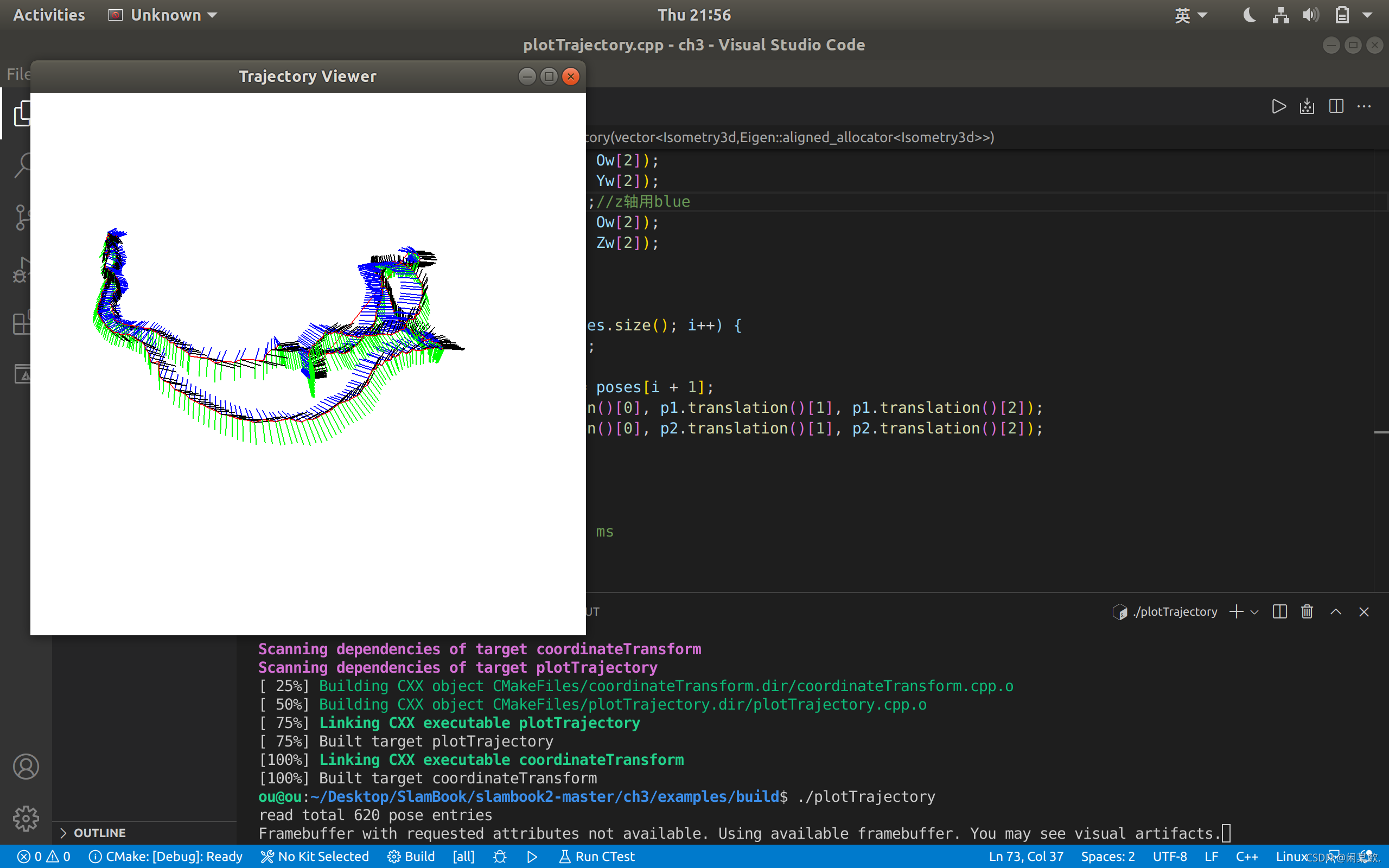
去掉了中间的连线

