//todo
/**
*IMU预积分中采用中值积分地推jacobian和covariance
**/
void midPointIntegration(double _dt,
const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0,
const Eigen::Vector3d &_acc_1, const Eigen::Vector3d &_gyr_1,
const Eigen::Vector3d &delta_p, const Eigen::Quaterniond &delta_q, const Eigen::Vector3d &delta_v,
const Eigen::Vector3d &linearized_ba, const Eigen::Vector3d &linearized_bg,
Eigen::Vector3d &result_delta_p, Eigen::Quaterniond &result_delta_q, Eigen::Vector3d &result_delta_v,
Eigen::Vector3d &result_linearized_ba, Eigen::Vector3d &result_linearized_bg, bool update_jacobian)
中值法计算预积分
处理IMU数据的函数。采用的是中值法计算预积分,对应的公式为

Vector3d un_acc_0 = delta_q * (_acc_0 - linearized_ba);//(4-1)
Vector3d un_gyr = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;//(5) w
result_delta_q = delta_q * Quaterniond(1, un_gyr(0) * _dt / 2, un_gyr(1) * _dt / 2, un_gyr(2) * _dt / 2);//(3)--->un_gyr(0) * _dt / 2 (5)
Vector3d un_acc_1 = result_delta_q * (_acc_1 - linearized_ba);//(4-2)
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);//(4)
result_delta_p = delta_p + delta_v * _dt + 0.5 * un_acc * _dt * _dt;//(1)
result_delta_v = delta_v + un_acc * _dt;//(2) --> un_acc(4)
result_linearized_ba = linearized_ba;
result_linearized_bg = linearized_bg;
推jacobian和covariance
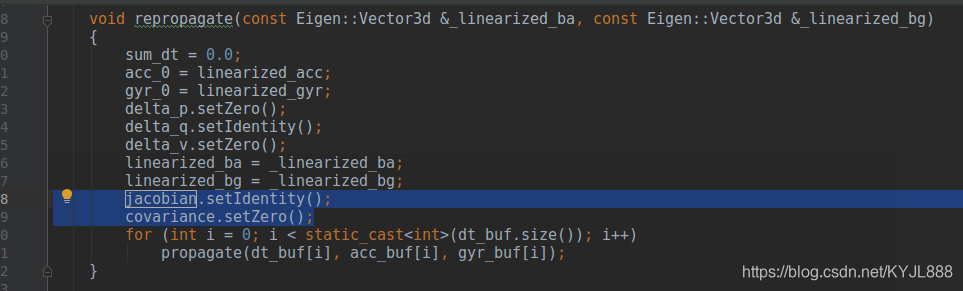
jacobian.setIdentity();
covariance.setZero();


R_w_x<<0, -w_x(2), w_x(1),
w_x(2), 0, -w_x(0),
-w_x(1), w_x(0), 0;//反对称矩阵
R_a_0_x<<0, -a_0_x(2), a_0_x(1),
a_0_x(2), 0, -a_0_x(0),
-a_0_x(1), a_0_x(0), 0;//反对称矩阵
R_a_1_x<<0, -a_1_x(2), a_1_x(1),
a_1_x(2), 0, -a_1_x(0),
-a_1_x(1), a_1_x(0), 0;//反对称矩阵
MatrixXd F = MatrixXd::Zero(15, 15);
F.block<3, 3>(0, 0) = Matrix3d::Identity();
F.block<3, 3>(0, 3) = -0.25 * delta_q.toRotationMatrix() * R_a_0_x * _dt * _dt +
-0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt * _dt;
F.block<3, 3>(0, 6) = MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(0, 9) = -0.25 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt * _dt;
F.block<3, 3>(0, 12) = -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * -_dt;
F.block<3, 3>(3, 3) = Matrix3d::Identity() - R_w_x * _dt;
F.block<3, 3>(3, 12) = -1.0 * MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(6, 3) = -0.5 * delta_q.toRotationMatrix() * R_a_0_x * _dt +
-0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt;
F.block<3, 3>(6, 6) = Matrix3d::Identity();
F.block<3, 3>(6, 9) = -0.5 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt;
F.block<3, 3>(6, 12) = -0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * -_dt;
F.block<3, 3>(9, 9) = Matrix3d::Identity();
F.block<3, 3>(12, 12) = Matrix3d::Identity();
//cout<<"A"<<endl<<A<<endl;

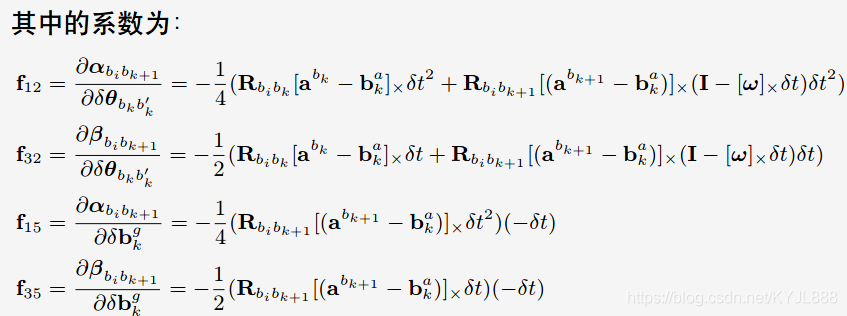
MatrixXd V = MatrixXd::Zero(15,18);
V.block<3, 3>(0, 0) = 0.25 * delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 3) = 0.25 * -result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * 0.5 * _dt;
V.block<3, 3>(0, 6) = 0.25 * result_delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 9) = V.block<3, 3>(0, 3);
V.block<3, 3>(3, 3) = 0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(3, 9) = 0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(6, 0) = 0.5 * delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 3) = 0.5 * -result_delta_q.toRotationMatrix() * R_a_1_x * _dt * 0.5 * _dt;
V.block<3, 3>(6, 6) = 0.5 * result_delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 9) = V.block<3, 3>(6, 3);
V.block<3, 3>(9, 12) = MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(12, 15) = MatrixXd::Identity(3,3) * _dt;
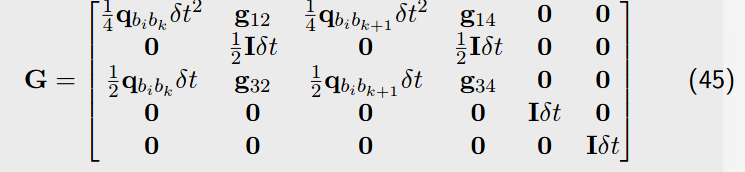
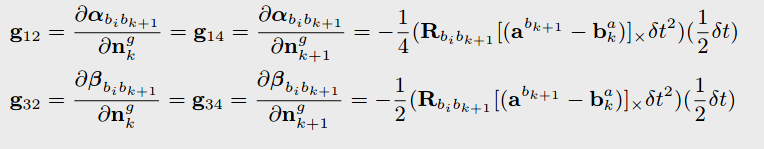
jacobian = F * jacobian;
covariance = F * covariance * F.transpose() + V * noise * V.transpose();

noise = Eigen::Matrix<double, 18, 18>::Zero();
noise.block<3, 3>(0, 0) = (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(3, 3) = (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(6, 6) = (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(9, 9) = (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(12, 12) = (ACC_W * ACC_W) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(15, 15) = (GYR_W * GYR_W) * Eigen::Matrix3d::Identity();
雅克比矩阵的使用

void EdgeImu::ComputeJacobians() {
...............
}
jacobians_[3] Eigen::Quaterniond corrected_delta_q /jacobian_speedbias_i
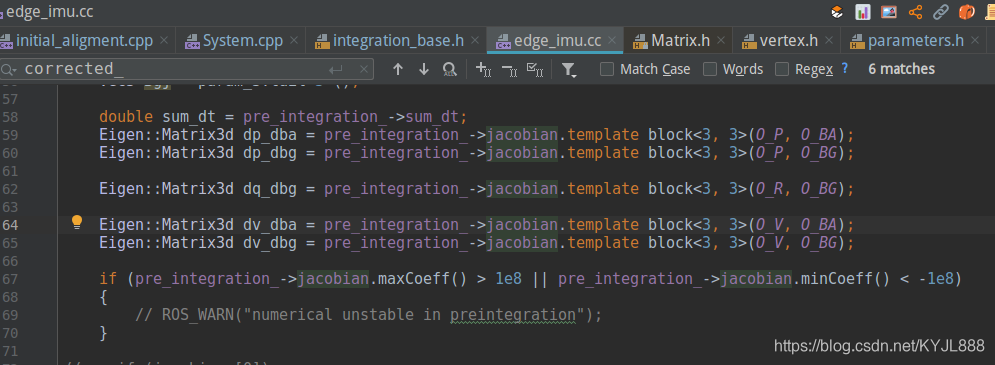
covariance的使用
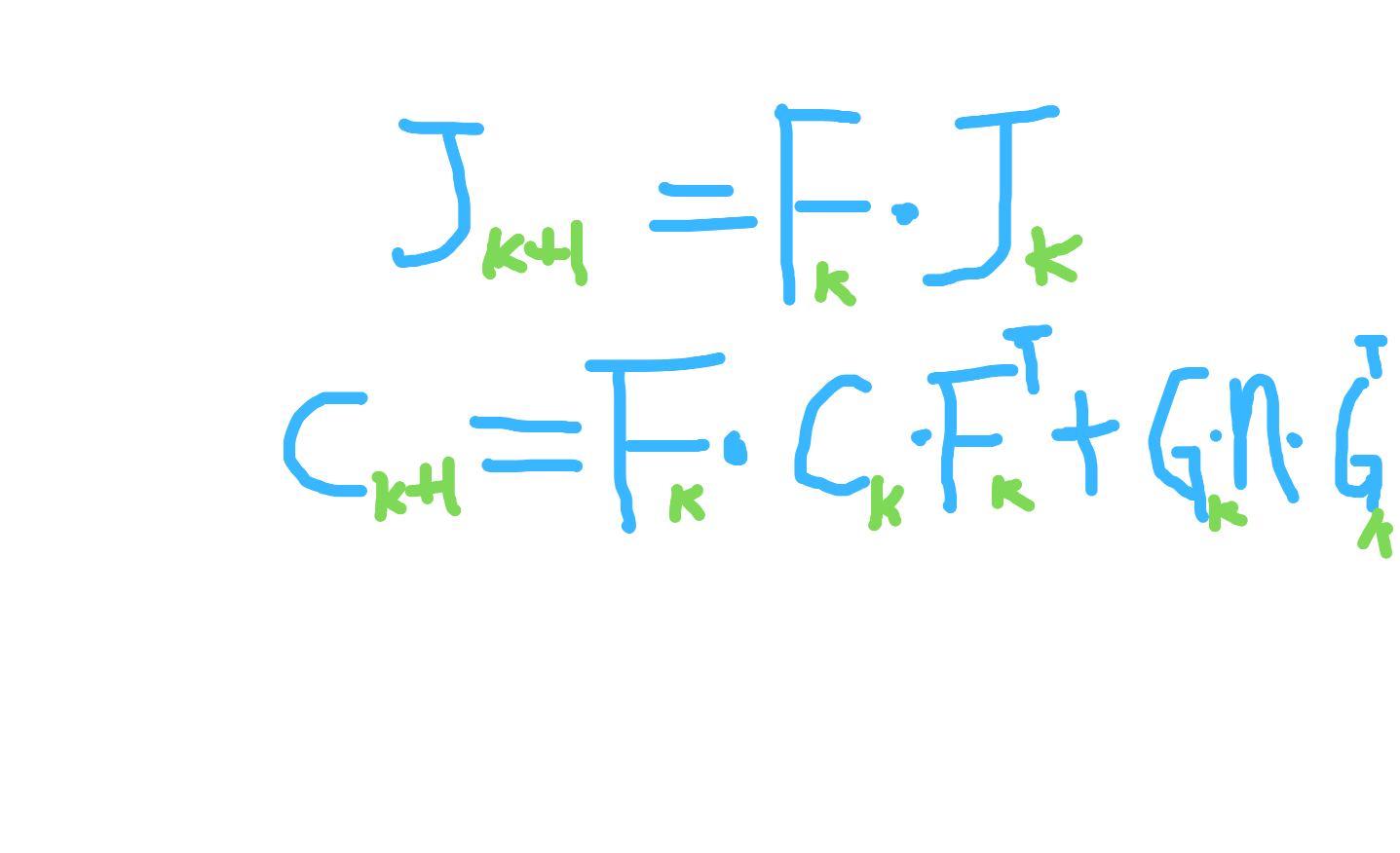
评估残差: residual = pre_integration->evaluate;
covariance = F * covariance * F.transpose() + V * noise * V.transpose(); Eigen::Map<Eigen::Matrix<double, 15, 1>> residual(residuals);
residual = pre_integration->evaluate(Pi, Qi, Vi, Bai, Bgi,
Pj, Qj, Vj, Baj, Bgj);
Eigen::Matrix<double, 15, 15> sqrt_info = Eigen::LLT<Eigen::Matrix<double, 15, 15>>(pre_integration->covariance.inverse()).matrixL().transpose();
//sqrt_info.setIdentity();
residual = sqrt_info * residual;计算残差中使用 (设置信息矩阵)
void EdgeImu::ComputeResidual() {
.....................
residual_ = pre_integration_->evaluate(Pi, Qi, Vi, Bai, Bgi,
Pj, Qj, Vj, Baj, Bgj);
// Mat1515 sqrt_info = Eigen::LLT< Mat1515 >(pre_integration_->covariance.inverse()).matrixL().transpose();
SetInformation(pre_integration_->covariance.inverse());
}edge.h
/// 返回残差
VecX Residual() const { return residual_; }
/// 返回雅可比
std::vector<MatXX> Jacobians() const { return jacobians_; }
/// 设置信息矩阵
void SetInformation(const MatXX &information) {
information_ = information;
// sqrt information
sqrt_information_ = Eigen::LLT<MatXX>(information_).matrixL().transpose();
}Eigen::LLT<MatXX>(information_)LLT.h
template<typename InputType>
explicit LLT(const EigenBase<InputType>& matrix)
: m_matrix(matrix.rows(), matrix.cols()),
m_isInitialized(false)
{
compute(matrix.derived());
}
信息矩阵
1. 协方差矩阵
在统计学中,
方差
是用来度量
单个随机变量
的
离散程度
,而协方差则一般用来刻画
两个随机变量
的
相似程度.
其中,
方差
的计算公式为
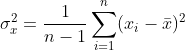
其中,n 表示样本量,符号
表示观测样本的均值。
在此基础上,
协方差
的计算公式被定义为
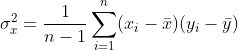
在公式中,符号
,
分别表示两个随机变量所对应的观测样本均值,据此,我们发现:方差
可视作随机变量
关于其自身的协方差 .
2. 信息矩阵和协方差矩阵
1:运动方程有协方差矩阵R,观测方程有协方差矩阵Q。它们表示的意义是,到当前时刻t为止,所有测量的样本的协方差矩阵,
用来衡量本次测量的不确定性
。
2:信息矩阵是协方差矩阵的逆,用来表示本次测量的可靠性,即
不确定越小,则可靠性就越大
。
3:因此,公式推导里出现的相邻两个状态之间的协方差矩阵,实际上是到当前状态为止,之前所有样本的协方差矩阵。也就是说协方差矩阵随着样本的增加在不断的更新。
3. 协方差矩阵和信息矩阵在SLAM中的应用
经过优化后,误差只是减少并不是完全消除,不能消除的误差去那了呢,当然是每条边分摊喽,那么问题来了,每条边误差分担多少呢,难道每条边都分担一样多的误差吗,当然也是可以的,但这样明显不科学,因为有些边在构建的时候已经很准确了,所以这个时候就有了信息矩阵,它表达的是每条边要分摊总误差的多少,嗯 ,这样就科学多了。提一句,如果你的信息矩阵是单位矩阵,那么误差就是均摊啦。(
误差项的权重
)
但是信息矩阵是协方差矩阵的一个逆矩阵,这个怎么理解呢?没什么意义,香农形式,这里是推导出来的,只是换了一种数学表达形式
,那为什么需要信息矩阵呢?
因为信息矩阵在计算条件概率分布明显比协方差矩阵要方便
,显然,协方差矩阵要求逆矩阵,所以时间复杂度是O(n^3). 之后我们可以在图优化slam中可以看到,因为图优化优化后的解是无穷多个的,比如说x1->x2->x3, 每个xi相隔1m这是我们实际观测出来的,优化后,我们会得出永远得不出x1 x2 x3的唯一解,因为他们有可能123 可能是234 blabla 但是如果我们提供固定值比如说x2 坐标是3那么解那么就有唯一解234,提供固定值x2这件事情其实就是个先验信息,提供先验信息,求分布,那就是条件分布,也就是这里我们要用到信息矩阵。
4.最小二乘计算误差
另外,因为是最小二乘计算误差,误差项取平方,所以
误差项的权重(信息矩阵)
也要对应σ的平方。
极大似然估计中,信息矩阵、Hessian矩阵和协方差矩阵的关系
1. Fisher Information Matrix 和 Hessian of Log Likelihood
这个博客
根据Fisher Information的定义,非常清晰地证明了为什么Fisher Information Matrix和负的Hessian of log likelihood是相等的(关键步骤是二阶导运算符和积分可以互换位置!)。
2. Hessian of Negative Log Likelihood 和 Covariance Matrix
高斯分布假设下,maximum likelihood的等效结果是minimize negative log likelihood(根据高斯分布的概率密度函数可以看出)。同时注意到,negative log likelihood的二阶导数(也就是其Hessian),正好是协方差的逆,也就是说此Hessian of Negative Log Likelihood即Inverse of Covariance Matrix。
这个结论可以继续往下推广:
当高斯分布的均值是关于状态的线性函数时,negative log likelihood的二阶导数(也就是其Hessian),正好是这个线性变换后的新状态的的协方差的逆,此时也有Hessian of Negative Log Likelihood (about the original state)
等于
Inverse of (new) Covariance Matrix。
当高斯分布的均值是关于状态的非线性函数时,可以做一个线性化将其展开乘线性形式,于是根据上一段的结论,此时Approximate Hessian of Negative Log Likelihood (about the original state)
等于
Approximate Inverse of (new) Covariance Matrix
近似于
Inverse of (new) Covariance Matrix。
另外,这里也有
一份pdf
阐述了我的上述理解。
3. 总结
注意到negative log likelihood其实就得到了我们非常熟悉的指标函数了,在高斯牛顿法中,指标函数做线性展开时得到的Hessian,实际就是前面所说的Approximate Hessian of Negative Log Likelihood (about the original state),这个Hessian,从一个方向近似等于Fisher信息矩阵,从另一个方向则近似等于协方差矩阵的逆。
REF:
1.
如何直观理解协方差矩阵
3.
OrbSLAM的Optimizer函数用到的信息矩阵如何理解
4.
SLAM优化中信息矩阵
5.
PCA中的协方差
6. 拓展学习:
高斯分布与边缘化