目录
一、浮点型和整型存储方式一样吗?
尝试着做一下,看答案是否和你想得相同,如果不一样,那你算是找对文章了。


答案1:是以整型的方式存储,以整型的方式取出
答案2:是以整型的方式存储,以浮点型的方式取出
答案3:是以浮点型的方式存储,以整型的方式取出
答案4:是以浮点型的方式存储,以浮点型的方式取出
由此我们可以得知,整型的存储方式和浮点型的存储方式是不一样的
二、浮点型的存储规则
2.1 S,M,E求法
根据国际标准IEEE 754,任何一个二进制的浮点数都能表示为以下方式
(-1)^S*M*2^E
浮点数为正数时S=0,反之S=1
M表示有效数字,在1~2之间(二进制)
2^E表示指数位
用一个实例来帮助大家理解
写出5.5对应的式子
5.5的二进制:101.1(小数点右边是从2的-1次方开始)
S=0(5.5为正数)
E=2(转换成科学计数法:1.011小数点左移两位)
M=1.011
既然浮点型可以用SEM来表示,那我们存放这三个值是不是就间接的把数据存在内存中了
所以在内存中存放浮点型就是在存放SME
2.2 如何存放S,M,E
2.2.1 IEEE 754规定
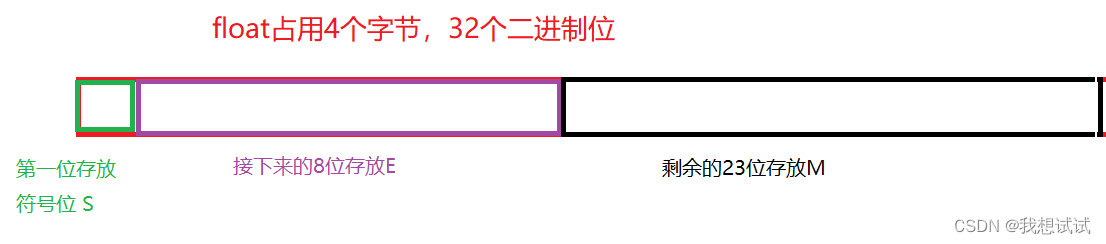
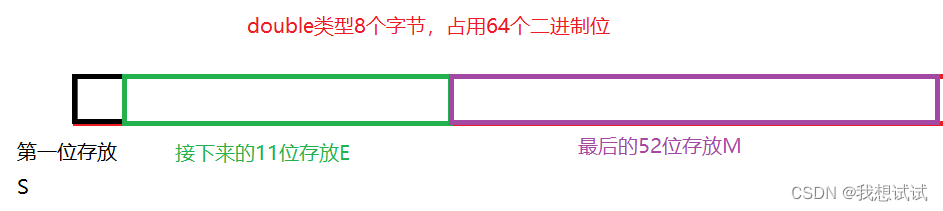
2.2.2 特别的规定
存储M
在我们取M时会将它转换为1.xxxxxxxx(范围在1~2之间的数),如此我们存储时会一直存放一个不变的数1
IEEE 754规定:
在计算机保存M时,默认他的第一位永远是1,因此可以将它舍去,
只存储小数点后的数据
,这样还可以提高精度
存储E
当我们在内存中存储E时,是从第二位开始的,没有符号位,所以它是一个无符号整数
当它占8位时(float)数据范围0~255,占11位时(double)数据范围0~2047
但是,我们在实际计算中
E是可能出现负数
的比如0.5
0.5的二进制:0.1
S:0
M:1.0(科学计数法的形式,小数点向右移1位)
E:-1
当E出现负数,但内存中
不能表示负数
,因为他是
无符号类型
的
IEEE 754规定:
再存入真实的E之前要加一个中间数,8位时加127,11位时加1023,如此就可以解决出现负数的情况
2.2.3 验证
我们进行一个简单的验证,同时让大家的记忆更加深刻

如果你在困惑内存中存放的为什么是倒过来的
这涉及到大小端的问题,在上一篇整型数据的存储时详细的讲解了这个问题,在此就不过多赘述
2.3 取出规则
2.3.1 E不全为0或不全为1
S:存的什么就取出什么
E:当E的范围是8位时(float),存的时候+127,取得时候-127,得到的就是真实值
当E的范围是11位时(double),存的时候+1023,取得时候-1023,得到的就是真实值
M:存的时候,只存了小数点右边的值,取出来的时候要在前面加上1
2.3.2 E为全0
S:存的什么就取出什么
E:直接用1-127(1-1023)就为真实值
M:不用在加前面的1,直接是0.xxxxxxx
2.3.3 E为全1
存放的是无穷大的数字,存取规则和第一种情况相同。
2.3.4验证
// 这个是上面5.5存进去的列子
// 0 10000001 01100000000000000000000
// S E M
// S =0 是正数
// E = (10000001)129 - 127 = 2
// M = 0.011+1 =1.011
// (-1)^S*M*2^E
// 由此可以写出对应的数字了解了怎样存储和取出浮点型数据,开头的那道程序是否有了不一样的见解


答案1和答案4
他们就是整型的方式存储,整型的方式取出,浮点型的方式存储,浮点型的方式取出
这里解析答案2和答案3
int main()
{
int n = 9;
float* pFloat = (float*)&n;
//整型方式存进去的是补码
//00000000000000000000000000001001 //9的原码,正数的原反补相同
//浮点型的方式取出,就认为里面存的是浮点类型,要用浮点型的规则取出
//0 00000000 00000000000000000001001
//S E M
//S = 0
//E = 1-127 = -126
//M = 0.00000000000000000001001
//(-1)*0*0.00000000000000000001001 *2^-128
//是一个非常小的数字接近于0,float精度不够,所以只能打印出0.000000
printf("*pFloat的值为:%f\n", *pFloat);
*pFloat = 9.0;
//浮点型的方式存进去,整型的方式取出来
//9的二进制:1001
// S = 0
// E = 3 +127 =130
// M = 1.001
//实际在内存中存储的是
//0 10000010 00100000000000000000000
//用整型的方式取出,就认为存进去的是补码(正数,原反补相同)
//01000001000100000000000000000000 (原码)
//原码换算成十进制为:1,091,567,616
printf("num的值为:%d\n", n);
return 0;
}
END.
有没有一种豁然开朗的感觉呢?有没有感觉到,生硬的规则下又透露出一丝丝的合理,让我对前辈们又多了一份敬佩。
如果对整型的存储有不清楚的地方,可以翻看我的另一篇文章.
最后送给大家一句名言:
Genius only means hard-working all one’s life. ——Mendeleyev Russian chemist
天才只意味着终身不懈地努力。——俄国化学家 门捷列耶夫