掌握机器学习数学基础之概率统计

机器学习为什么要使用概率
概率学派和贝叶斯学派
何为随机变量和何又为概率分布？
条件概率，联合概率和全概率公式：
边缘概率
独立性和条件独立性
期望、方差、协方差和相关系数
常用概率分布
贝叶斯及其应用
中心极限定理
极大似然估计
概率论中的独立同分布?

机器下学习为什么要使用概率

我们借助概率论来解释分析机器学习为什么是这样的，有什么依据，同时反过来借助概率论来推导出更多机器学习算法。很多人说机器学习是老中医，星座学，最主要的原因是机器学习的很多不可解释性，我们应用概率知识可以解释一部分，但还是很多值得我们去解释理解的东西，同时，什么时候机器学习更多的可解释了，反过来，可以用那些理论也可以继续为机器学习的，对人工智能创造推出更多的理论，等到那一天，也许真的能脱离更多的人工智障了。
这是因为机器学习通常必须处理不确定量,有时也可能需要处理随机 (非确定性的) 量。不确定性和随机性可能来自多个方面。总结如下，

不确定性有三种可能的来源：

被建模系统内在的随机性：例如一个假想的纸牌游戏，在这个游戏中我们假设纸牌被真正混洗成了随机顺序。假如这个时候你要对这个这个游戏建模(预测抽的牌点数也好，预测怎么玩才会赢也罢)，虽然牌的数量和所有牌有什么是确定的，但是若我们随机抽一张，这个牌是什么是随机的。这个时候就要使用概率去建模了。
不完全观测：例如一个游戏节目的参与者被要求在三个门之间选择，并且会赢得放置在选中门后的奖品。其中两扇门通向山羊，第三扇门通向一辆汽车。选手的每个选择所导致的结果是确定的，但是站在选手的角度，结果是不确定的。在机器学习中也是这样，很多系统在预测的时候，是不确定的，这个时候我们就要用一个”软度量“即概率去描述它。
不完全建模：假设我们制作了一个机器人，它可以准确地观察周围每一个对象的位置。在对这些对象将来的位置进行预测时，如果机器人采用的是离散化的空间，那么离散化的方法将使得机器人无法确定对象们的精确位置：因为每个对象都可能处于它被观测到的离散单元的任何一个角落。也就是说，当不完全建模时，我们不能明确的确定结果，这个时候的不确定，就需要概率来补充。

频率学派和贝叶斯学派：

简单的理解的话：

频率学派：研究的是事件本身，所以研究者只能反复试验去逼近它从而得到结果。比如：想要计算抛掷一枚硬币时正面朝上的概率，我们需要不断地抛掷硬币，当抛掷次数趋向无穷时正面朝上的频率即为正面朝上的概率。

贝叶斯学派：研究的是观察者对事物的看法，所以你可以用先验知识和收集到的信息去描述他，然后用一些证据去证明它。还是比如抛硬币，当小明知道一枚硬币是均匀的，然后赋予下一次抛出结果是正面或反面都是50%的可信度（概率分布），可能是出于认为均匀硬币最常见这种信念，然后比如小明随机抛了1000次，发现结果正是这样，那么它就通过这些证据验证了自己的先验知识。（也有存在修改的时候，比如发现硬币的材质不一致，总之就是这么一个过程）

不是很懂？那我们继续举起”栗子“来：如果一个医生诊断了病人，并说该病人患流感的几率为40%，这就不好办了，因为这意味着非常不同的事情——我们既不能让病人有无穷多的副本，也没有任何理由去相信病人的不同副本在具有不同的潜在条件下表现出相同的症状。若我们用概率来表示一种信任度，其中1表示非常肯定病人患有流感，而0表示非常肯定病人没有流感。这样医生也就变的好办了。然后前面那种概率，直接与事件发生的频率相联系，被称为频率派概率；而后者，涉及到确定性水平，被称为贝叶斯概率。（当然，这知识举例，不是说贝叶斯学派优于概率学派）

来个比喻：概率学派像唯物主义，世间事物不会以你的意识的转移而转变，概率就是事物客观的存在的现象。

贝叶斯学派就是我思故我在，同一个事件，对于观察者来说，他若知道，那就是确定性事件，如果不知道，就是随机事件，鬼知道它到底存不存在。

总的来说，两个学派站的角度不一样，贝叶斯概率论为人的知识（knowledge）建模来定义概率这个概念。频率学派试图描述的是事物本体，而贝叶斯学派试图描述的是观察者知识状态在新的观测发生后如何更新，描述的是观察这的对事物看法。

何为随机变量和何又为概率分布？

随机变量：随机变量可以随机地取不同值的变量。我们通常用小写字母来表示随机变量本身，而用带数字下标的小写字母来表示随机变量能够取到的值。例如，
$x_{1}$
和
$x_{2}$
都是随机变量X可能的取值。

对于向量值变量，我们会将随机变量写成
$X$
，它的一个值为
$x$
。就其本身而言，一个随机变量只是对可能的状态的描述；它必须伴随着一个概率分布来指定每个状态的可能性。

随机变量可以是离散的或者连续的。离散随机变量拥有有限或者可数无限多的状态。注意这些状态不一定非要是整数;它们也可能只是一些被命名的状态而没有数值。连续随机变量伴随着实数值。注意：下面很多在知识点都会分离散和连续的分别讲述，但其实原理类似。

当随机变量是离散的，我们称是离散型随机变量，如果是连续的，我们会说是连续型随机变量。

举例：比如，一次掷20个硬币，k个硬币正面朝上，k是随机变量，k的取值只能是自然数0，1，2，…，20，而不能取小数3.5、无理数√20，因而k是离散型随机变量。

公共汽车每15分钟一班，某人在站台等车时间x是个随机变量，x的取值范围是[0,15)，它是一个区间，从理论上说在这个区间内可取任一实数3.5、√20等，因而称这随机变量是连续型随机变量。

概率分布：给定某随机变量的取值范围，概率分布就是导致该随机事件出现的可能性。而从机器学习的角度来说的话，概率分布就是符合随机变量取值范围的某个对象属于某个类别或服从某种趋势的可能性。

条件概率，联合概率和全概率公式：

条件概率：其记号为P(A|B)，表示在给定条件B下A事件发生的概率。

举个“栗子”：P(第二次投硬币是正面|第一次投硬币是正面)：就是在“第一次投硬币是正面”时“第二次投硬币是正面”的概率。不过，既然举了这个例子，那么就顺带问一下：你以为P(第二次投硬币是正面|第一次投硬币是正面)的结果是多少呢？1/4？错。答案是1/2，是不是很意外？看完下面的两种情况你就明白了。

条件概率的两种情况：

B事件的结果不会影响到A事件的发生。如上面的例子，两次投币正面向上的概率不会相互干扰。所以A事件发生的概率=A事件单独发生的概率。记为：P(A|B) =P(A)
B事件的结果会影响A事件的发生。如：若头天下雨，则第二天下雨的可能性会增大。即：A事件在B事件之后发生的概率> A事件单独发生的概率。记为：P(A|B)> P(A)

条件概率链式法则:

任何多维随机变量的联合概率分布，都可以分解成只有一个变量的条件概率相乘的形式：

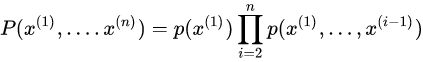
这个规则被称为概率的链式法则或者乘法法则。它可以直接从条件概率的定义中得到。例如，使用两次定义可以得到

$p(a,b,c)=p(a|b,c)p(b,c)$

$p(b,c)=p(b|c)p(c)$

$p(a,b,c)=p(a|b,c)p(b|c)p(c)$

联合概率：联合概率为两个事件同时发生的概率。记为：P(A and B)或直接P(AB)

然后，因为两个事件的发生会有先后，所以联合概率可以进一步描述为：“事件A发生的概率”和“事件A发生后，事件B发生的概率”。于是：P(A and B)= P(A)P(B|A)

结合刚才“条件概率的两种情况”，可以得出：P(A and B) 根据不同的情况有如下两种结果：

P(A and B) = P(A)P(B) — A和B的结果互不影响，即：P(B|A) = P(B)
P(A and B) = P(A)P(B|A) — 反之

全概率公式：公式表示若事件B1，B2，…，Bn构成一个完备事件组且都有正概率，则对任意一个事件A都有公式成立。注意：

Bi

是两两互斥的，如下图：

举例：某地盗窃风气盛行，且偷窃者屡教不改。我们根据过往的案件记录，推断A今晚作案的概率是0.8，B今晚作案的概率是0.1，C今晚作案的概率是0.5，除此之外，还推断出A的得手率是0.1，B的得手率是1.0，C的得手率是0.5。那么，今晚村里有东西被偷的概率是多少？

通过阅读上述文字，我们大概对A、B、C三人有了一个初步的印象。首先，A的脑子可能有些问题，特别喜欢偷，但是技术相当烂。B看来是个江湖高手，一般不出手，一出手就绝不失手。C大概是追求中庸，各方面都很普通。

我们将文字描述转换为数学语言，根据作案频率可知

P

(

A

)=0.8,

P

(

B

)=0.1,

P

(

C

)=0.5

将“村里有东西被偷”记为

S

，根据得手率可以得到

P

(

S

|

A

)=0.1,

P

(

S

|

B

)=1.0,

P

(

S

|

C

)=0.5

很简单，所求得的就是

P

(

S

)=

P

(

A

)

P

(

S

|

A

)+

P

(

B

)

P

(

S

|

B

)+

P

(

C

)

P

(

S

|

C

)=0.43

祝这个村晚上好运吧。

边缘概率

边缘概率：当我们知道一组变量的联合概率分布时，若我们想知道一个子集的概率分布。那么定义在子集上的概率分布就被我们称为边缘概率分布。

离散型随机变量： X和Y，并且我们知道P(X, Y)。我们可以依据下面的求和法则来计算P(x)

$\forall x\in X，P(X=x)=\sum_{y}^{}{X=x，Y=y}$

注：这里有了大写字母表示随机变量，但其实要用小写的，具体查看上面第一节。

注：“边缘概率”的名称来源于手算边缘概率的计算过程。当P(x, y)的每个值被写在由每行表示不同的x值，每列表示不同的y值形成的网格中时，对网格中的每行求和是很自然的事情，然后将求和的结果P(x)写在每行右边的纸的边缘处。

连续型随机变量：我们需要用积分替代求和：

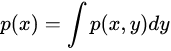
独立性和条件独立性

独立性：两个随机变量 x和y，如果它们的概率分布可以表示成两个因子的乘积形式,并且一个因子只包含x另一个因子只包含y，,我们就称这两个随机变量是相互独立的：

$\forall x\in X,y\in Y,p(X=x,Y=y)=p(X=x)p(Y=y)$

条件独立性：如果关于 x 和 y 的条件概率分布对于 z 的每一个值都可以写成乘积的形式,那么这两个随机变量 x 和 y 在给定随机变量 z 时是条件独立的(conditionally independent):

$\forall x\in X,y\in Y,z\in Z,p(X=x,Y=y|Z=z)=p(X=x|Z=z)p(Y=y|Z=z)$

我们可以采用一种简化形式来表示独立性和条件独立性:x⊥y 表示 x 和 y 相互独立,x⊥y | z 表示 x 和 y 在给定 z 时条件独立。

期望、方差、协方差和相关系数

在概率论和统计学中，数学期望是试验中每次可能结果的概率乘以其结果的总和。它是最基本的数学特征之一，反映随机变量平均值的大小。

离散随机变量：假设X是一个离散随机变量，其可能的取值有：
$\left\{ x_{1} ,x_{2} ,......,x_{n} \right\}$
，各个取值对应的概率取值为：
$P\left( x_{k} \right) , k=1,2,......,n$
，则其数学期望被定义为：

$E\left(X \right) =\sum_{k=1}^{n}{x_{k} P\left( x_{k} \right) }$

举例说明：

某城市有10万个家庭，没有孩子的家庭有1000个，有一个孩子的家庭有9万个，有两个孩子的家庭有6000个，有3个孩子的家庭有3000个。

则此城市中任一个家庭中孩子的数目是一个随机变量，记为X。它可取值0，1，2，3。

其中，X取0的概率为0.01，取1的概率为0.9，取2的概率为0.06，取3的概率为0.03。

则，它的数学期望

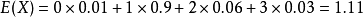
即此城市一个家庭平均有小孩1.11个。

连续型随机变量：假设X是一个连续型随机变量，其概率密度函数为
$P\left( x \right)$
则其数学期望被定义为：

$E\left( x \right) =\int_{-\varpi }^{+\varpi } xf\left( x \right) dx$

方差：概率中，方差用来衡量随机变量与其数学期望之间的偏离程度；统计中的方差为样本方差，是各个样本数据分别与其平均数之差的平方和的平均数。数学表达式如下：

$Var\left( x \right) =E\left\{ \left[ x-E\left( x \right) \right] ^{2} \right\} =E\left( x^{2} \right) -\left[ E\left( x \right) \right] ^{2}$

协方差：在概率论和统计学中，协方差被用于衡量两个随机变量X和Y之间的总体误差。数学定义式为：

$Cov\left( X,Y \right) =E\left[ \left( X-E\left[ X \right] \right) \left( Y-E\left[ Y \right] \right) \right] =E\left[ XY \right] -E\left[ X \right] E\left[ Y \right]$

相关系数：相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量。由于研究对象的不同，相关系数有如下几种定义方式。

简单相关系数：又叫相关系数或线性相关系数，一般用字母r 表示，用来度量两个变量间的线性关系。定义式：

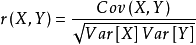
其中，Cov(X,Y)为X与Y的协方差，Var[X]为X的方差，Var[Y]为Y的方差

常用概率分布

伯努利试验（Bernoulli experiment）：是在同样的条件下重复地、相互独立地进行的一种随机试验，其特点是该随机试验只有两种可能结果：发生或者不发生。

（1）离散型随机变量分布：

0-1分布：

0-1分布是单个二值型离散随机变量的分布，其概率分布函数为：

$P\left( X=1 \right) =p$
$P\left( X=0 \right) =1-p$

几何分布

几何分布是离散型概率分布，其定义为：在n次伯努利试验中，试验k次才得到第一次成功的机率。即：前k-1次皆失败，第k次成功的概率。其概率分布函数为：

$P\left( X=k \right) =\left( 1-p \right) ^{k-1} p$

性质，这个需要记住：

$E\left( X \right) =\frac{1}{p}$
$Var\left( X \right) =\frac{1-p}{p^{2} }$

二项分布

二项分布即重复n次伯努利试验，各次试验之间都相互独立，并且每次试验中只有两种可能的结果，而且这两种结果发生与否相互对立。如果每次试验时，事件发生的概率为p，不发生的概率为1-p，则n次重复独立试验中发生k次的概率为：

$P\left( X=k \right) =C_{n}^{k} p^{k} \left( 1-p \right) ^{n-k}$

性质：

$E\left( X \right) =np$
$Var\left( X \right) =np\left( 1-p \right)$

泊松分布

日常生活中，大量事件是有固定频率的，比如：

某医院平均每小时出生3个婴儿
某网站平均每分钟有2次访问
某超市平均每小时销售4包奶粉

它们的特点就是，我们可以预估这些事件的总数，但是没法知道具体的发生时间。已知平均每小时出生3个婴儿，请问下一个小时，会出生几个？有可能一下子出生6个，也有可能一个都不出生，这是我们没法知道的。

泊松分布就是描述某段时间内，事件具体的发生概率。其概率函数为：

$P\left( N\left( t \right) =n \right) =\frac{\left( \lambda t \right) ^{n}e^{-\lambda t} }{n!}$

其中：

P表示概率，N表示某种函数关系，t表示时间，n表示数量，1小时内出生3个婴儿的概率，就表示为 P(N(1) = 3) ；λ 表示事件的频率。

还是以上面医院平均每小时出生3个婴儿为例，则
$\lambda =3$
；

那么，接下来两个小时，一个婴儿都不出生的概率可以求得为：

$P\left( N\left(2 \right) =0 \right) =\frac{\left( 3\cdot 2 \right) ^{o} \cdot e^{-3\cdot 2} }{0!} \approx 0.0025$

同理，我们可以求接下来一个小时，至少出生两个婴儿的概率：

$P\left( N\left( 1 \right) \geq 2 \right) =1-P\left( N\left( 1 \right)=0 \right) - P\left( N\left( 1 \right)=1 \right)\approx 0.8$

（2）连续型随机变量分布：

均匀分布

在概率论和统计学中，均匀分布也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。均匀分布由两个参数a和b定义，它们是数轴上的最小值和最大值，通常缩写为U（a，b）

均匀分布的概率密度函数为：

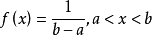
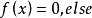
高斯分布/正态分布

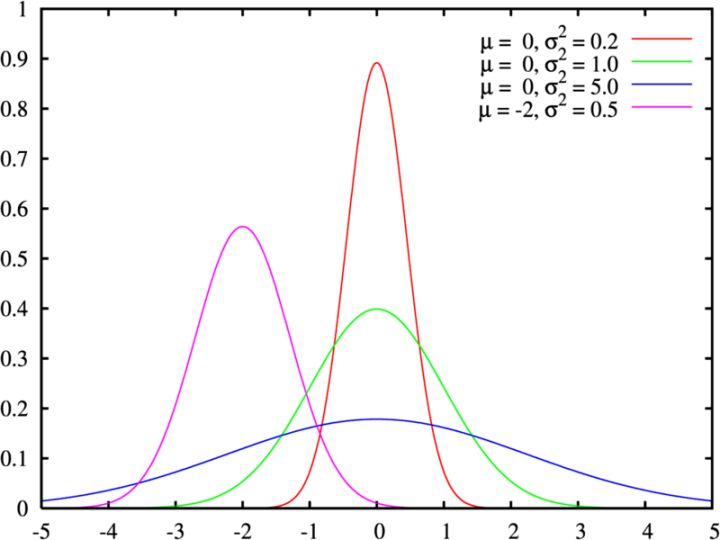
高斯分布又叫正态分布，其曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，如下图所示的这个不同期望和方差的分布图：

若随机变量X服从一个数学期望为
$\mu$
，方差为
$\sigma ^{2}$
的正态分布，则我们将其记为：
$N\left( \mu ,\sigma^{2} \right)$
。其期望值
$\mu$
决定了正态分布的位置，其标准差
$\sigma$
（方差的开方）决定了正态分布的幅度。

就如上图：σ描述正态分布资料数据分布的离散程度，σ越大，数据分布越分散，σ越小，数据分布越集中。也称为是正态分布的形状参数，σ越大，曲线越扁平，反之，σ越小，曲线越瘦高。

而对应的，一维正态分布，且其概率密度函数为：

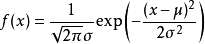
注：高斯分布是几个及其重要的分布，希望读者可以去深入了解。

指数分布

指数分布是事件的时间间隔的概率，它的一个重要特征是无记忆性。这个是其最重要的性质！例如：如果某一元件的寿命的寿命为T，已知元件使用了t小时，它总共使用至少t+s小时的条件概率，与从开始使用时算起它使用至少s小时的概率相等。下面这些都属于指数分布：

婴儿出生的时间间隔
网站访问的时间间隔
奶粉销售的时间间隔

指数分布的公式可以从泊松分布推断出来。如果下一个婴儿要间隔时间t，就等同于t之内没有任何婴儿出生，即：

$P\left( X\geq t \right) =P\left( N\left( t \right) =0 \right) =\frac{\left( \lambda t \right) ^{0}\cdot e^{-\lambda t} }{0!}=e^{-\lambda t}$

则：

$P\left( X\leq t \right) =1-P\left( X\geq t \right) =1-e^{-\lambda t}$

如：接下来15分钟，会有婴儿出生的概率为：

$P\left( X\leq \frac{1}{4} \right) =1-e^{-3\cdot \frac{1}{4} } \approx 0.53$

指数分布的图像如下：

贝叶斯及其应用

”栗子“引申出知识：曲奇饼问题

条件：碗1中有30个香草曲奇饼干和10个巧克力饼干，碗2中有上述饼干个20个。

问：闭上眼随机拿一块，从碗1中拿到香草曲奇的概率是多少？

解：首先，我们将“问”的内容用数学符号表示出来，即：P(碗1|香草)。

PS1：这里我对为什么是“P(碗1|香草)”而不是“P(香草|碗1)”有点疑惑，个人感觉将问题描述成“得到的是香草饼干，而且该饼干是从碗1中拿到的”会更好。

PS2：顺便一提P(香草|碗1) = 3/4。嗯？为什么？从碗1出拿出一块饼干是香草饼干的概率这不是显而易见的 3/4 么，这个和碗2完全没关系。

然后，我们计算P(碗1|香草)。。。。。这怎么算？嗯。。香草饼干一共50块，巧克力饼干一共30块，所以取出一块饼干是香草的概率是5/8 然后。。然后。。饼干从碗1中取出的概率是1/2。

不行我编不下去了，还是看看书上怎么说的吧(其实上面这两个概率就是贝叶斯公式中的两个必求的概率)。（翻书翻书）书上说的求这个要用贝叶斯定理。

那我们先把这个问题暂停到这里，看一下贝叶斯定理。

贝叶斯定理

介绍：贝叶斯定理是一种“根据数据集内容的变化而更新假设概率”的方法。

于是对于事件A和B，贝叶斯定理的表达式可写成：

$P\left( B|A \right) =\frac{P\left( A|B \right)P\left( B\right) }{P\left( A \right) }$

在这种解释里，每项的意义如下：

P(B)：先验概率。即：在的得到新数据前某一假设的概率。

P(B|A)：后验概率。即：在看到新数据后，要计算的该假设的概率。

P(A|B) ：似然度。即：在该假设下，得到这一数据的概率。

P(A)：标准化常亮。即：在任何假设下得到这一数据的概率。

额。。不太好理解啊。那我们还用香草饼干的例子来说明下。我们求得是P(碗1|香草)，所以上面的A对应的事件是“取出饼干的碗是碗1”，B对应的事件是“取出的饼干是香草饼干”。于是：

先验概率P(B) ：取出饼干的碗是碗1的概率。结果是1/2。

后验概率P(B|A) ：得到的是香草饼干，且该饼干从碗1中拿到。待求。

似然度P(A|B)：在碗1中得到香草饼干的概率。结果是3/4。

标准化常亮P(A)：饼干是香草饼干的概率。结果是5/8。

现在，上面这四个除了待求的后验概率外其他的求已经知道了！那这就好办了，我们代入公式，于是很容易就得出结果了。

中心极限定理

中心极限定理：是概率论中的一组定理。中央极限定理说明，大量相互独立的随机变量，其均值的分布以正态分布为极限。这组定理是数理统计学和误差分析的理论基础，指出了大量随机变量之和近似服从正态分布的条件。

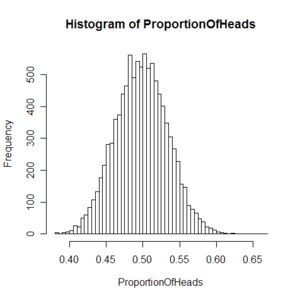
本图描绘了多次抛掷硬币实验中出现正面的平均比率，每次实验均抛掷了大量硬币。我们就可以发现其是符合高斯分布的。

极大似然估计

最大似然估计：是利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值的一种方法。

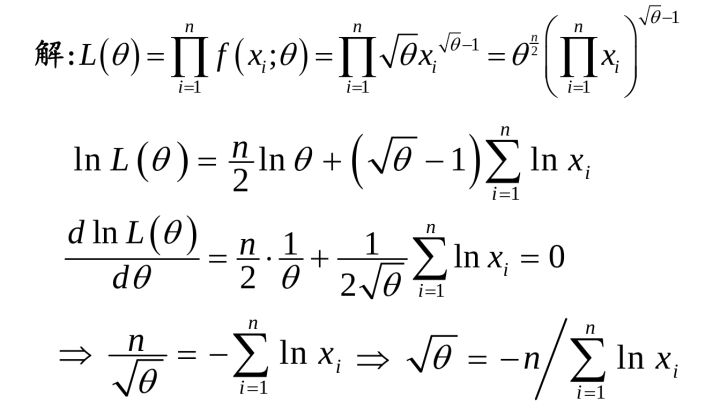
上面有定义和例子，应该比较好理解了，我们要注意的是离散型和联系型的区别。这个知识点特别重要，机器学习很多时候，应该说是非常多时候，都是在求参调参。怎么求参，很多时候用就是极大似然估计！

概率论中的独立同分布?

独立：就是每次抽样之间是没有关系的,不会相互影响。就像我抛色子每次抛到几就是几这就是独立的。但若我要两次抛的和大于8,其余的不算,那么第一次抛和第二次抛就不独立了,因为第二次抛的时候结果是和第一次相关的。不懂可查看独立性。

同分布：就是每次抽样,样本都服从同样的一个分布抛色子每次得到任意点数的概率都是1/6,这就是同分布的但若我第一次抛一个六面的色子,第二次抛一个正12面体的色子,就不再是同分布了

独立同分布：就是每次抽样之间独立而且同分布的意思

追问：同分布是指服从同一分布函数么？答：是的。

转载于:https://www.cnblogs.com/jialin0421/p/8988834.html