博客

使用示例：

输入[input]：[5 4 3 2 1 1 1 1]

输出[output]：

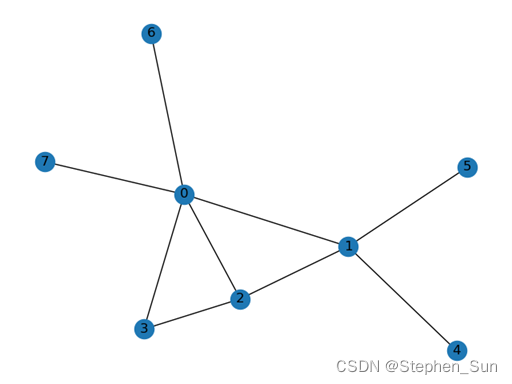
相关实现代码如下：

'''
通过软件界面输入任意一个有限非负整数序列，
如果是图序列，界面上显示一个对应的简单图，
否则，界面上显示“否”。
'''
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt

seq_input = [int(n) for n in input("输入一个序列：").split()]  # 输入一个序列
seq_input.sort(reverse=True)  # 将输入的序列降序排列
print("序列按降序排列：", seq_input)

# 若序列的和为奇数，则不是图的度序列
sum_seq_input = np.sum(seq_input)
if sum_seq_input % 2 == 1:
    print("该序列不是图序列！")
else:
    seq_input = np.array(seq_input)  # 将输入转化为np数组
    seq_len = seq_input.size  # 获取序列长度
    n = seq_len
    matrix_adj = np.zeros((n, n))  # 生成一个nxn的邻接矩阵
    matrix_iter = np.array([seq_input])  # 初始化序列矩阵，保存每一次循环过后的序列结果

    ite_num = 0
    # 循环求解删除第一个点以及对应的边后的子图的序列
    while ((seq_input < 0).any() == False) & ((seq_input == 0).all() == False):

        # 当最大度点的度数大于n-1时，不存在简单图
        if (seq_input[0]+1) > n:
            print("该序列不是图序列！")
            break

        # 循环次数计数
        ite_num = ite_num + 1
        print("第", ite_num, "轮递归")

        # 执行简单图度序列判定算法
        for i in range(0, seq_input[0]+1):
            seq_input[i] = seq_input[i]-1
        seq_input = np.delete(seq_input, 0)  # 删去剩余序列的第一个点
        n = n-1
        # 由于np.sort函数只能升序排列，因此对其相反数进行升序排列后再取相反数
        seq_input = np.sort(-seq_input)
        seq_input = (-seq_input)
        print(seq_input)

        # 更新序列矩阵
        d_inst = np.pad(seq_input, (ite_num, 0), 'constant', constant_values=(0, 0))
        matrix_iter = np.insert(matrix_iter, ite_num, values=d_inst, axis=0)

    # 循环结束，判断是否是全0还是有负数
    if (seq_input < 0).any():
        print("该序列不是图序列！")
    elif (seq_input == 0).all():

        # 当可以是图序列的时候，利用迭代矩阵更新邻接矩阵
        for i in range(ite_num-1, -1, -1):  # 行遍历
            for k in range(i+1, seq_len, 1):  # 列遍历
                matrix_adj[i, k] = matrix_iter[i, k] - matrix_iter[i+1, k]
                matrix_adj[k, i] = matrix_iter[i, k] - matrix_iter[i+1, k]
        print("该序列对应的图的邻接矩阵：")
        print(matrix_adj)

        # 使用networkx进行绘图
        G = nx.Graph()
        Matrix = matrix_adj

        # 当邻接矩阵中对应的点之间的值为1时，在两点之间添加一条边
        for i in range(len(Matrix)):
            for j in range(len(Matrix)):
                if Matrix[i, j] == 1:
                  G.add_edge(i, j)

        nx.draw(G, with_labels=True)
        plt.show()