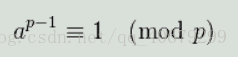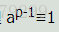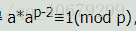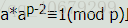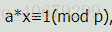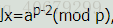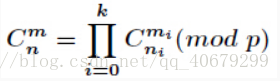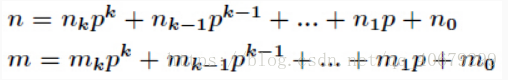在开始之前我们先介绍3个定理:
1.乘法逆元
如果ax≡1 (mod p),且gcd(a,p)=1(a与p互质),则称a关于模p的乘法逆元为x。
2.费马小定理:
3.扩展欧几里得
已知整数a、b,扩展欧几里得算法可以在求得a、b的最大公约数的同时,能找到整数x、y(其中一个很可能是负数),使它们满足贝祖等式ax + by = gcd(a, b)。
好了,在明白上面的定理后我们开始分析乘法逆元:ax≡1 (mod p) 这个等式用中文描述就是 a乘一个数x并模p等于1,即 a%p*x%p=res,res%p=1;看上去就是同余定理的一个简单等式- -。那么问题来了。
———————————————————————————————————————————–
为什么可以用费马小定理来求逆元呢?
由费马小定理
, 变形得
,答案已经很明显了:若a,p互质,因为
且
,则
,用快速幂可快速求之。
———————————————————————————————————————————–
为什么可以用扩展欧几里得求得逆元?
我们都知道模就是余数,比如12%5=12-5*2=2,18%4=18-4*4=2。(/是程序运算中的除)
那么ax≡1 (mod p)即ax-yp=1.把y写成+的形式就是ax+py=1,为方便理解下面我们把p写成b就是ax+by=1。就表示x是a的模b乘法逆元,y是b的模a乘法逆元。然后就可以用扩展欧几里得求了。
———————————————————————————————————————————–
知道逆元怎么算之后,那么乘法逆元有什么用呢?
先说重点,本人认为!乘法逆元最大的作用就是,在要除以一个数,再取模时,把除法变成乘法运算,然后再取模。因为除法,比如用16/5应该是3.2,但是计算机会算成3.。。误差有没有,用double就更不用说了,数大了一定有误差,所以,有了逆元!!!!
若对于数字A,C 存在X,使A * X = 1 (mod C) ,那么称X为 A 对C的乘法逆元。
逆元的作用?让我们来看下面的例子:
12 / 4 mod 7 = ? 很显然结果是3
我们现在对于数对 (4,7), 可以知道 X = 2是 4 对7的乘法逆元即2*4=1(mod 7)
那么我们有(12 / 4) * (4 * 2 ) = (?) * (1) (mod 7)
除法被完美地转化为了乘法
理论依据:
F / A mod C = ?
如果存在 A*X = 1 (mod C)
那么2边同时乘起来,得到 F * X = ? (mod C)
成立条件
(1) 模方程 A * X = 1(mod C) 存在解
(2) A | F (F % A == 0)
以下来百度百科:
若ax=1 mod f 则称a关于模f的乘法逆元为x。也可表示为ax≡1(mod f)。
当a与f互素时,a关于模f的乘法逆元有唯一解。如果不互素,则无解。如果f为素数,则从1到f-1的任意数都与f互素,即在1到f-1之间都恰好有一个关于模f的乘法逆元。
例如,求5关于模14的乘法逆元:
14=5*2+4
5=4+1
说明5与14互素,存在5关于14的乘法逆元。
1=5-4=5-(14-5*2)=5*3-14
因此,5关于模14的乘法逆元为3。
———————————————————————————————————————————–
接下来进入正题:
Lucas定理针对该取值范围较大又不太大的情况
定理描述
这样将组合数的求解分解为小问题的乘积,下面考虑计算C(ni, mi) %p.
已知C(n, m) mod p = n!/(m!(n – m)!) mod p。当我们要求(a/b)mod p的值,且b很大,无法直接求得a/b的值时,我们可以转而使用乘法逆元k,将a乘上k再模p,即(a*k) mod p。 其结果与(a/b) mod p等价。
下面附上Lucas定理的一种证明,见下图,参考冯志刚《初等数论》第37页。
对于该定理的理解,也很好理解:
其实大可不必看中间一大堆文字描述,直接看下面公式的推导:
———————————————————————————————————————————–
代码实现:
费马小定理实现(其实跟拓展gcd没多大区别,换了个公式而已)
#include <iostream>
#include <stdio.h>
#include <algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
ll mulit(ll a,ll b,ll m){
ll ans=0;
while(b){
if(b&1) ans=(ans+a)%m;
a=(a<<1)%m;
b>>=1;
}
return ans;
}
ll quick_mod(ll a,ll b,ll m){
ll ans=1;
while(b){
if(b&1){
ans=mulit(ans,a,m);
}
a=mulit(a,a,m);
b>>=1;
}
return ans;
}
ll comp(ll a,ll b,ll m){
if(a<b) return 0;
if(a==b) return 1;
if(b>a-b) b=a-b;
ll ans=1,ca=1,cb=1;
for(int i=0;i<b;i++){
ca=ca*(a-i)%m;
cb=cb*(b-i)%m;
}
ans=ca*quick_mod(cb,m-2,m)%m;
return ans;
}
ll lucas(ll a,ll b,ll m){
ll ans=1;
while(a&&b){
ans=(ans*comp(a%m,b%m,m))%m;
a/=m;
b/=m;
}
return ans;
}
int main()
{
ll a,b,m;
while(cin>>a>>b>>m){
cout<<lucas(a,b,m)<<endl;
}
return 0;
}
拓展gcd实现
#include <iostream>
#include <stdio.h>
#include <algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
ll exgcd(ll a,ll b,ll& x,ll& y){
if(a%b==0){
x=0,y=1;
return b;
}
ll r,tx,ty;
r=exgcd(b,a%b,tx,ty);
x=ty;
y=tx-a/b*ty;
}
ll comp(ll a,ll b,ll m){
if(a<b) return 0;
if(a==b) return 1;
if(b>a-b) b=a-b;
ll ans=1,ca=1,cb=1;
for(int i=0;i<b;i++){
ca=ca*(a-i)%m;
cb=cb*(b-i)%m;
}
ll x,y;
exgcd(cb,m,x,y);
x=(x%m+m)%m;
ans=ca*x%m;
return ans;
}
ll lucas(ll a,ll b,ll m){
ll ans=1;
while(a&&b){
ans=(ans*comp(a%m,b%m,m))%m;
a/=m;
b/=m;
}
return ans;
}
int main()
{
ll a,b,m;
int n;
cin>>n;
while(n--){
cin>>a>>b>>m;
cout<<lucas(a+b,b,m)<<endl;
}
return 0;
}
试试拓展吧
拓展卢卡斯定理