信用评分模型可用“四张卡”来表示,分别是 A卡(Application score card,申请评分卡)、B卡(Behavior score card,行为评分卡)、C卡(Collection score card,催收评分卡)和 F卡(Anti-Fraud Card,反欺诈评分卡),分别应用于贷前、贷中、贷后。
本篇我们主要讨论基于Python的信用评分模型开发,并在各部分附上了相关代码。
❶
项目流程
典型的信用评分模型如图1-1所示。信用风险评级模型的主要开发流程如下:
1.数据获取,
包括获取存量客户及潜在客户的数据。存量客户是指已开展相关业务的客户;潜在客户是指未来拟开展相关业务的客户。
2.数据预处理
,主要工作包括数据清洗、缺失值处理、异常值处理,主要是为了将获取的原始数据转化为可用作模型开发的格式化数据。
3.探索性数据分析
,该步骤主要是获取样本总体的大概情况,描述样本总体情况的指标主要有直方图、箱形图等。
4.变量选择
,该步骤主要是通过统计学的方法,筛选出对违约状态影响最显著的指标。主要有单变量特征选择方法和基于机器学习模型的方法。
5.模型开发
,该步骤主要包括变量分段、变量的WOE(证据权重)变换和逻辑回归估算三部分。
6.模型评估
,该步骤主要是评估模型的区分能力、预测能力、稳定性,并形成模型评估报告,得出模型是否可以使用的结论。
7.信用评分,
根据逻辑回归的系数和WOE等确定信用评分的方法。将Logistic模型转换为标准评分的形式。
8.建立评分系统
,根据信用评分方法,建立自动信用评分系统。
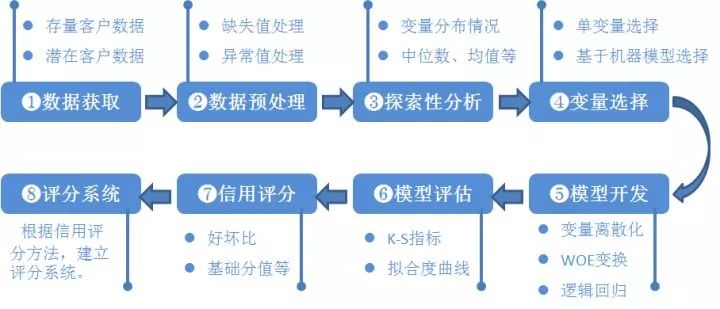
图1-1 信用评分模型开发流程
❷
数据获取
数据来自Kaggle的Give Me Some Credit:https://www.kaggle.com/c/GiveMeSomeCredit/data,有15万条的样本数据,下图可以看到这份数据的大致情况。
数据属于个人消费类贷款,只考虑信用评分最终实施时能够使用到的数据应从如下一些方面获取数据:
– 基本属性:包括了借款人当时的年龄。
– 偿债能力:包括了借款人的月收入、负债比率。
– 信用往来:两年内35-59天逾期次数、两年内60-89天逾期次数、两年内90天或高于90天逾期的次数。
– 财产状况:包括了开放式信贷和贷款数量、不动产贷款或额度数量。
– 贷款属性:暂无。
– 其他因素:包括了借款人的家属数量(不包括本人在内)。
– 时间窗口:自变量的观察窗口为过去两年,因变量表现窗口为未来两年。
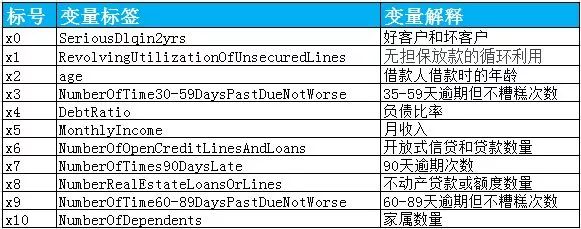
图2-1 原始数据的变量
#
❸
数据预处理
在对数据处理之前,需要对数据的缺失值和异常值情况进行了解。Python内有describe()函数,可以了解数据集的缺失值、均值和中位数等。
-
#载入数据
-
data = pd.read_csv('cs-training.csv')
-
#数据集确实和分布情况
-
data.describe().to_csv('DataDescribe.csv')
数据集的详细情况:

图3-1 变量详细情况
从上图可知,变量 MonthlyIncome 和 NumberOfDependents 存在缺失,变量 MonthlyIncome 共有缺失值 29731 个,NumberOfDependents 有 3924 个缺失值。
3.1
缺失值处理
这种情况在现实问题中非常普遍,这会导致一些不能处理缺失值的分析方法无法应用,因此,在信用风险评级模型开发的第一步我们就要进行缺失值处理。缺失值处理的方法,包括如下几种。
**1.直接删除含有缺失值的样本。
2.根据样本之间的相似性填补缺失值。
3.根据变量之间的相关关系填补缺失值。**
变量 MonthlyIncome 缺失率比较大,所以我们根据变量之间的相关关系填补缺失值,我们采用随机森林法:
-
# 用随机森林对缺失值预测填充函数
-
def set_missing(df):
-
# 把已有的数值型特征取出来
-
process_df = df.ix[:,[5,0,1,2,3,4,6,7,8,9]]
-
# 分成已知该特征和未知该特征两部分
-
known = process_df[process_df.MonthlyIncome.notnull()].as_matrix()
-
unknown = process_df[process_df.MonthlyIncome.isnull()].as_matrix()
-
# X为特征属性值
-
X = known[:, 1:]
-
# y为结果标签值
-
y = known[:, 0]
-
# fit到RandomForestRegressor之中
-
rfr = RandomForestRegressor(random_state=0,
-
n_estimators=200,max_depth=3,n_jobs=-1)
-
rfr.fit(X,y)
-
# 用得到的模型进行未知特征值预测
-
predicted = rfr.predict(unknown[:, 1:]).round(0)
-
print(predicted)
-
# 用得到的预测结果填补原缺失数据
-
df.loc[(df.MonthlyIncome.isnull()), 'MonthlyIncome'] = predicted
-
return df
NumberOfDependents 变量缺失值比较少,直接删除,对总体模型不会造成太大影响。对缺失值处理完之后,删除重复项。
-
data=set_missing(data)#用随机森林填补比较多的缺失值
-
data=data.dropna()#删除比较少的缺失值
-
data = data.drop_duplicates()#删除重复项
-
data.to_csv('MissingData.csv',index=False)
3.2
异常值处理
缺失值处理完毕后,我们还需要进行异常值处理。
异常值是指明显偏离大多数抽样数据的数值
,比如个人客户的年龄为0时,通常认为该值为异常值。找出样本总体中的异常值,通常采用离群值检测的方法。
首先,我们发现变量age中存在0,显然是异常值,直接剔除:
-
# 年龄等于0的异常值进行剔除
-
data = data[data['age'] > 0]
对于变量 NumberOfTime30-59DaysPastDueNotWorse、NumberOfTimes90DaysLate 、NumberOfTime60-89DaysPastDueNotWorse 这三个变量,由下面的箱线图图 3-2 可以看出,均存在异常值,且由 unique 函数可以得知均存在 96、98 两个异常值,因此予以剔除。同时会发现剔除其中一个变量的 96、98 值,其他变量的 96、98 两个值也会相应被剔除。
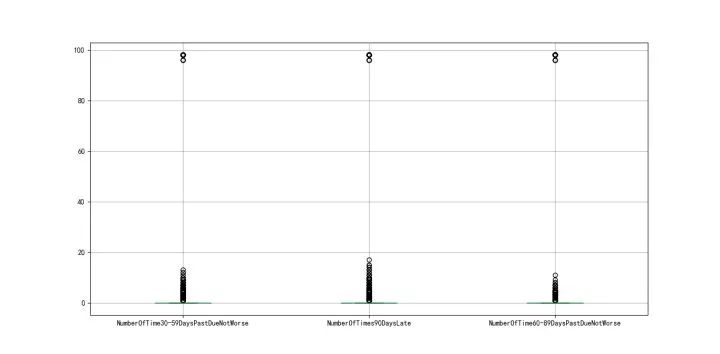
图3-2 箱形图
剔除变量 NumberOfTime30-59DaysPastDueNotWorse 、 NumberOfTimes90DaysLate 、 NumberOfTime60-89DaysPastDueNotWorse 的异常值。另外,数据集中好客户为 0,违约客户为 1,考虑到正常的理解,能正常履约并支付利息的客户为 1,所以我们将其取反。
-
#剔除异常值
-
data = data[data['NumberOfTime30-59DaysPastDueNotWorse'] < 90]
-
#变量SeriousDlqin2yrs取反
-
data['SeriousDlqin2yrs']=1-data['SeriousDlqin2yrs']
3.3
数据切分
为了验证模型的拟合效果,我们需要对数据集进行切分,分成
训练集和测试集
。
-
from sklearn.cross_validation import train_test_splitY = data['SeriousDlqin2yrs']
-
X = data.ix[:, 1:]
-
#测试集占比30%
-
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=0)
-
# print(Y_train)
-
train = pd.concat([Y_train, X_train], axis=1)
-
test = pd.concat([Y_test, X_test], axis=1)
-
clasTest = test.groupby('SeriousDlqin2yrs')['SeriousDlqin2yrs'].count()
-
train.to_csv('TrainData.csv',index=False)
-
test.to_csv('TestData.csv',index=False)
❹
探索性分析
在建立模型之前,我们一般会对现有的数据进行 EDA(Exploratory Data Analysis,探索性数据分析) 。EDA 是指对已有的数据(特别是调查或观察得来的原始数据)在尽量少的先验假定下进行探索。
常用的探索性数据分析方法有:直方图、散点图和箱线图等。
客户年龄分布如图4-1所示,可以看到年龄变量大致呈正态分布,符合统计分析的假设。
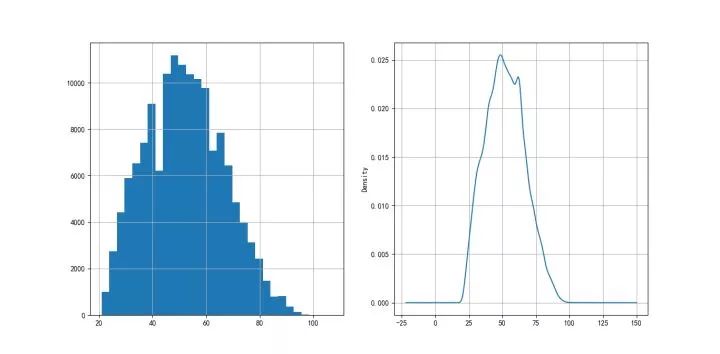
图4-1 客户年龄分布
客户年收入分布如图4-2所示,月收入也大致呈正态分布,符合统计分析的需要。
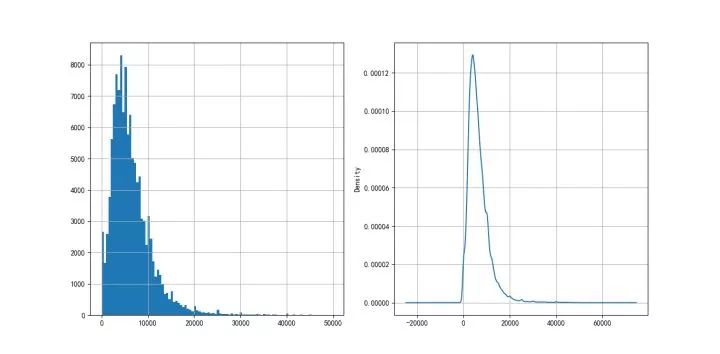
客户年收入分布如图4-2所示,月收入也大致呈正态分布,符合统计分析的需要。
❺
变量选择
特征变量选择(排序)对于数据分析、机器学习从业者来说非常重要。好的特征选择能够提升模型的性能,更能帮助我们理解数据的特点、底层结构,这对进一步改善模型、算法都有着重要作用。至于Python的变量选择代码实现可以参考结合Scikit-learn介绍几种常用的特征选择方法:https://www.cnblogs.com/hhh5460/p/5186226.html。
在本文中,我们采用信用评分模型的变量选择方法,通过
WOE分析方法,即是通过比较指标分箱和对应分箱的违约概率来确定指标是否符合经济意义
。首先我们对变量进行离散化(分箱)处理。
5.1
分箱处理
变量分箱
(binning)是对连续变量离散化(discretization)的一种称呼。信用评分卡开发中一般有常用的等距分段、等深分段、最优分段。
其中
等距分段
(Equval length intervals)是指分段的区间是一致的,比如年龄以十年作为一个分段;
等深分段
(Equal frequency intervals)是先确定分段数量,然后令每个分段中数据数量大致相等;
最优分段
(Optimal Binning)又叫监督离散化(supervised discretizaion),使用递归划分(Recursive Partitioning)将连续变量分为分段,背后是一种基于条件推断查找较佳分组的算法。
我们首先选择对连续变量进行最优分段,在连续变量的分布不满足最优分段的要求时,再考虑对连续变量进行等距分段。最优分箱的代码如下:
-
# 定义自动分箱函数def mono_bin(Y, X, n = 20):
-
r = 0
-
good=Y.sum()
-
bad=Y.count() - good
-
while np.abs(r) < 1:
-
d1 = pd.DataFrame({"X": X, "Y": Y, "Bucket": pd.qcut(X, n)})
-
d2 = d1.groupby('Bucket', as_index = True)
-
r, p = stats.spearmanr(d2.mean().X, d2.mean().Y)
-
n = n - 1
-
d3 = pd.DataFrame(d2.X.min(), columns = ['min'])
-
d3['min']=d2.min().X
-
d3['max'] = d2.max().X
-
d3['sum'] = d2.sum().Y
-
d3['total'] = d2.count().Y
-
d3['rate'] = d2.mean().Y
-
d3['woe']=np.log((d3['rate']/(1-d3['rate']))/(good/bad))
-
d4 = (d3.sort_index(by = 'min')).reset_index(drop=True)
-
print("=" * 60)
-
print(d4)
-
return d4
针对我们将使用最优分段对于数据集中的 RevolvingUtilizationOfUnsecuredLines 、age、 DebtRatio和MonthlyIncome 进行分类。
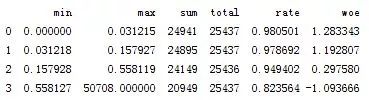
图5-1 RevolvingUtilizationOfUnsecuredLines分箱情况
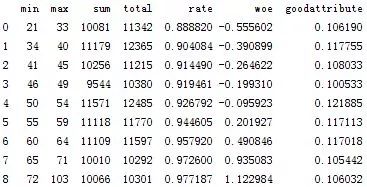
图5-2 age分箱情况
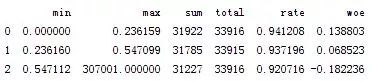
图5-3 DebtRatio分箱情况
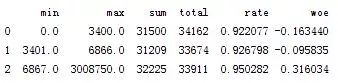
图5-4 MonthlyIncome分箱情况
针对不能最优分箱的变量,分箱如下:
-
# 连续变量离散化
-
cutx3 = [ninf, 0, 1, 3, 5, pinf]
-
cutx6 = [ninf, 1, 2, 3, 5, pinf]
-
cutx7 = [ninf, 0, 1, 3, 5, pinf]
-
cutx8 = [ninf, 0,1,2, 3, pinf]
-
cutx9 = [ninf, 0, 1, 3, pinf]
-
cutx10 = [ninf, 0, 1, 2, 3, 5, pinf]
5.2
WOE
WOE分析, 是对指标分箱、计算各个档位的WOE值并观察WOE值随指标变化的趋势。其中WOE的数学定义是:
woe=ln(goodattribute/badattribute)
在进行分析时,我们需要对各指标从小到大排列,并计算出相应分档的 WOE 值
。其中正向指标越大,WOE 值越小;反向指标越大,WOE 值越大。正向指标的 WOE 值负斜率越大,反响指标的正斜率越大,则说明指标区分能力好。WOE 值趋近于直线,则意味指标判断能力较弱。若正向指标和 WOE 正相关趋势、反向指标同 WOE 出现负相关趋势,则说明此指标不符合经济意义,则应当予以去除。
WOE函数实现在上一节的mono_bin()函数里面已经包含,这里不再重复。
5.3
相关性分析和IV筛选
接下来,我们会用经过清洗后的数据看一下变量间的相关性。注意,这里的相关性分析只是初步的检查,进一步检查模型的 VI (证据权重)作为变量筛选的依据。
相关性图我们通过Python里面的seaborn包,调用heatmap()绘图函数进行绘制,实现代码如下:
-
corr = data.corr()
-
#计算各变量的相关性系数
-
xticks = ['x0','x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']#x轴标签
-
yticks = list(corr.index)
-
#y轴标签
-
fig = plt.figure()ax1 = fig.add_subplot(1, 1, 1)sns.heatmap(corr, annot=True, cmap='rainbow', ax=ax1, annot_kws={'size': 9, 'weight': 'bold', 'color': 'blue'})
-
#绘制相关性系数热力图
-
ax1.set_xticklabels(xticks, rotation=0, fontsize=10)ax1.set_yticklabels(yticks, rotation=0, fontsize=10)plt.show()
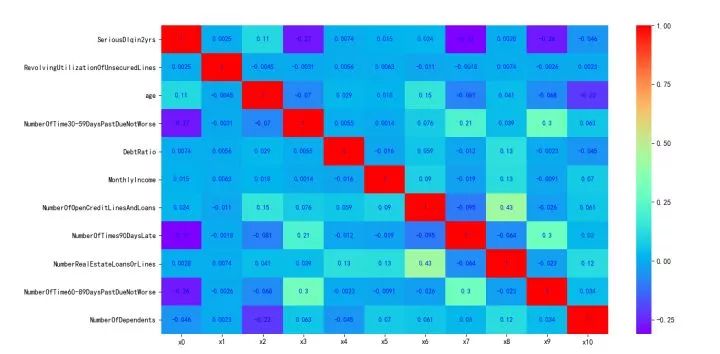
图5-5 数据集各变量的相关性
由上图可以看出,各变量之间的相关性是非常小的。NumberOfOpenCreditLinesAndLoans 和 NumberRealEstateLoansOrLines 的相关性系数为 0.43 。
接下来,
进一步计算每个变量的 Infomation Value(IV) 。
IV 指标是一般用来确定自变量的预测能力。其公式为:
IV=sum((goodattribute-badattribute)*ln(goodattribute/badattribute))
通过IV值判断变量预测能力的标准是:
< 0.02: unpredictive
0.02 to 0.1: weak
0.1 to 0.3: medium
0.3 to 0.5: strong
0.5: suspicious
IV的实现放在mono_bin()函数里面,代码实现如下:
-
# 定义自动分箱函数def mono_bin(Y, X, n = 20):
-
r = 0
-
good=Y.sum()
-
bad=Y.count()-good
-
while np.abs(r) < 1:
-
d1 = pd.DataFrame({"X": X, "Y": Y, "Bucket": pd.qcut(X, n)})
-
d2 = d1.groupby('Bucket', as_index = True)
-
r, p = stats.spearmanr(d2.mean().X, d2.mean().Y)
-
n = n - 1
-
d3 = pd.DataFrame(d2.X.min(), columns = ['min'])
-
d3['min']=d2.min().X
-
d3['max'] = d2.max().X
-
d3['sum'] = d2.sum().Y
-
d3['total'] = d2.count().Y
-
d3['rate'] = d2.mean().Y
-
d3['woe']=np.log((d3['rate']/(1-d3['rate']))/(good/bad))
-
d3['goodattribute']=d3['sum']/good
-
d3['badattribute']=(d3['total']-d3['sum'])/bad
-
iv=((d3['goodattribute']-d3['badattribute'])*d3['woe']).sum()
-
d4 = (d3.sort_index(by = 'min')).reset_index(drop=True)
-
print("=" * 60)
-
print(d4)
-
cut=[]
-
cut.append(float('-inf'))
-
for i in range(1,n+1):
-
qua=X.quantile(i/(n+1))
-
cut.append(round(qua,4))
-
cut.append(float('inf'))
-
woe=list(d4['woe'].round(3))
-
return d4,iv,cut,woe
生成的IV图代码:
-
ivlist=[ivx1,ivx2,ivx3,ivx4,ivx5,ivx6,ivx7,ivx8,ivx9,ivx10]
-
#各变量
-
IVindex=['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']
-
#x轴的标签
-
fig1 = plt.figure(1)ax1 = fig1.add_subplot(1, 1, 1)x = np.arange(len(index))+1ax1.bar(x, ivlist, width=0.4)
-
#生成柱状图
-
ax1.set_xticks(x)ax1.set_xticklabels(index, rotation=0, fontsize=12)ax1.set_ylabel('IV(Information Value)', fontsize=14)
-
#在柱状图上添加数字标签
-
for a, b in zip(x, ivlist):
-
plt.text(a, b + 0.01, '%.4f' % b, ha='center', va='bottom', fontsize=10)plt.show()
输出图像:
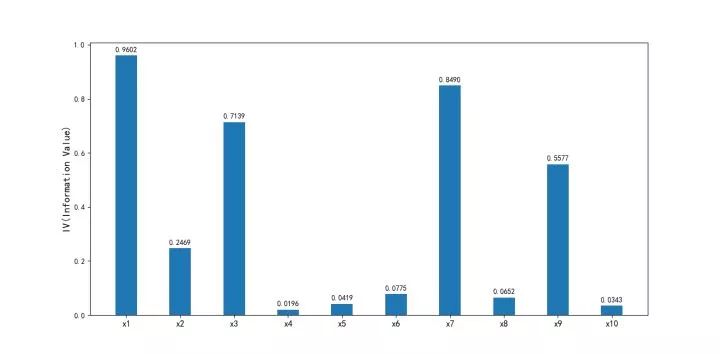
图5-6 输出的各变量IV图
可以看出, DebtRatio、 MonthlyIncome、 NumberOfOpenCreditLinesAndLoans、 NumberRealEstateLoansOrLines 和 NumberOfDependents 变量的IV值明显较低,所以予以删除。
❻
模型分析
证据权重(Weight of Evidence,WOE)转换可以将Logistic回归模型转变为标准评分卡格式。
引入WOE转换的目的并不是为了提高模型质量,只是一些变量不应该被纳入模型,或者是因为它们不能增加模型值,再或者是因为与其模型相关系数有关的误差较大,其实建立标准信用评分卡也可以不采用WOE转换。
这种情况下,Logistic回归模型需要处理更大数量的自变量。尽管这样会增加建模程序的复杂性,但最终得到的评分卡都是一样的。
在建立模型之前,我们需要将筛选后的变量转换为WOE值,便于信用评分。
6.1
WOE转换
我们已经能获取了每个变量的分箱数据和 WOE 数据,只需要根据各变量数据进行替换,实现代码如下:
-
#替换成woe函数def replace_woe(series, cut, woe):
-
list = []
-
I = 0
-
while i<len(series):
-
value=series[i]
-
j=len(cut) - 2
-
m=len(cut) - 2
-
while j >= 0:
-
if value>=cut[j]:
-
j = -1
-
else:
-
j -= 1
-
m -= 1
-
list.append(woe[m])
-
i += 1
-
return list
我们将每个变量都进行替换,并将其保存到 WoeData.csv 文件中:
-
# 替换成
-
woedata['RevolvingUtilizationOfUnsecuredLines'] = Series(replace_woe(data['RevolvingUtilizationOfUnsecuredLines'], cutx1, woex1))
-
data['age'] = Series(replace_woe(data['age'], cutx2, woex2))
-
data['NumberOfTime30-59DaysPastDueNotWorse'] = Series(replace_woe(data['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, woex3))
-
data['DebtRatio'] = Series(replace_woe(data['DebtRatio'], cutx4, woex4))
-
data['MonthlyIncome'] = Series(replace_woe(data['MonthlyIncome'], cutx5, woex5))
-
data['NumberOfOpenCreditLinesAndLoans'] = Series(replace_woe(data['NumberOfOpenCreditLinesAndLoans'], cutx6, woex6))
-
data['NumberOfTimes90DaysLate'] = Series(replace_woe(data['NumberOfTimes90DaysLate'], cutx7, woex7))
-
data['NumberRealEstateLoansOrLines'] = Series(replace_woe(data['NumberRealEstateLoansOrLines'], cutx8, woex8))
-
data['NumberOfTime60-89DaysPastDueNotWorse'] = Series(replace_woe(data['NumberOfTime60-89DaysPastDueNotWorse'], cutx9, woex9))
-
data['NumberOfDependents'] = Series(replace_woe(data['NumberOfDependents'], cutx10, woex10))
-
data.to_csv('WoeData.csv', index=False)
6.2
Logisic模型建立
我们直接调用 statsmodels 包来实现逻辑回归:
-
导入数据data = pd.read_csv('WoeData.csv')
-
#应变量
-
Y=data['SeriousDlqin2yrs']
-
#自变量,剔除对因变量影响不明显的变量
-
X=data.drop(['SeriousDlqin2yrs','DebtRatio','MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines','NumberOfDependents'],axis=1)
-
X1=sm.add_constant(X)
-
logit=sm.Logit(Y,X1)
-
result=logit.fit()
-
print(result.summary())
输出结果:
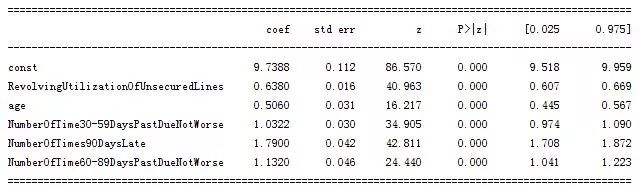
图6-1 逻辑回归模型结果
通过图 6-1 可知,逻辑回归各变量都已通过显著性检验,满足要求。
6.3
模型检验
到这里,我们的建模部分基本结束了。我们需要验证一下模型的预测能力如何。我们使用在建模开始阶段预留的 test 数据进行检验。通过 ROC 曲线和 AUC 来评估模型的拟合能力。
在 Python 中,可以利用 sklearn.metrics,它能方便比较两个分类器,自动计算 ROC 和 AUC 。
实现代码:
-
#应变量
-
Y_test = test['SeriousDlqin2yrs']
-
#自变量,剔除对因变量影响不明显的变量,与模型变量对应
-
X_test = test.drop(['SeriousDlqin2yrs', 'DebtRatio', 'MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines', 'NumberOfDependents'], axis=1)
-
X3 = sm.add_constant(X_test)
-
resu = result.predict(X3)
-
#进行预测
-
fpr, tpr, threshold = roc_curve(Y_test, resu)
-
rocauc = auc(fpr, tpr)
-
#计算
-
AUCplt.plot(fpr, tpr, 'b', label='AUC = %0.2f' % rocauc)
-
#生成ROC曲线
-
plt.legend(loc='lower right')
-
plt.plot([0, 1], [0, 1], 'r--')
-
plt.xlim([0, 1])
-
plt.ylim([0, 1])
-
plt.ylabel('真正率')
-
plt.xlabel('假正率')
-
plt.show()
输出结果:
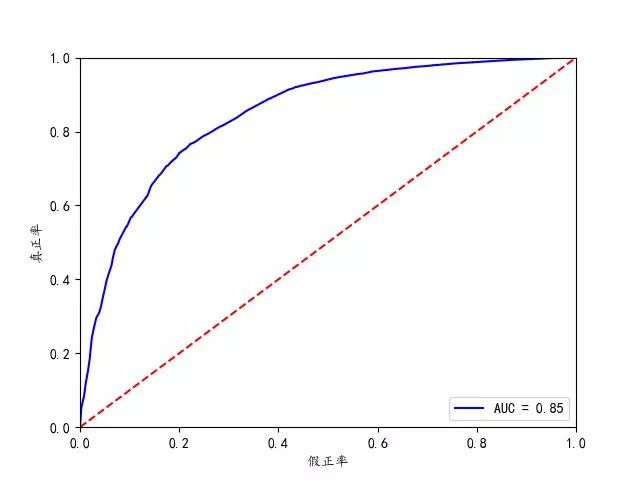
图6-2 ROC曲线
从上图可知,AUC 值为 0.85,说明该模型的预测效果还是不错的,正确率较高。
❼
信用评分
我们已经基本完成了建模相关的工作,并用ROC曲线验证了模型的预测能力。接下来的步骤,就是将Logistic模型转换为标准评分卡的形式。
7.1
评分标准

依据以上论文资料得到:
a=log(p_good/P_bad)
Score = offset + factor * log(odds)
在建立标准评分卡之前,我们需要选取几个评分卡参数:基础分值、 PDO (比率翻倍的分值)和好坏比。这里, 我们取600分为基础分值, PDO 为20 (每高20分好坏比翻一倍),好坏比取 20 。
-
# 我们取600分为基础分值,PDO为20(每高20分好坏比翻一倍),好坏比取20。
-
z = 20 / math.log(2)
-
q = 600 - 20 * math.log(20) / math.log(2)
-
baseScore = round(q + p * coe[0], 0)
个人总评分=基础分+各部分得分
7.2部分评分
下面计算各变量部分的分数。各部分得分函数:
-
#计算分数函数 def get_score(coe,woe,factor):
-
scores=[]
-
for w in woe:
-
score=round(coe*w*factor,0)
-
scores.append(score)
-
return scores
计算各变量得分情况:
-
# 各项部分分数
-
x1 = get_score(coe[1], woex1, p)
-
x2 = get_score(coe[2], woex2, p)
-
x3 = get_score(coe[3], woex3, p)
-
x7 = get_score(coe[4], woex7, p)
-
x9 = get_score(coe[5], woex9, p)
我们可以得到各部分的评分卡如图 7-1 所示:
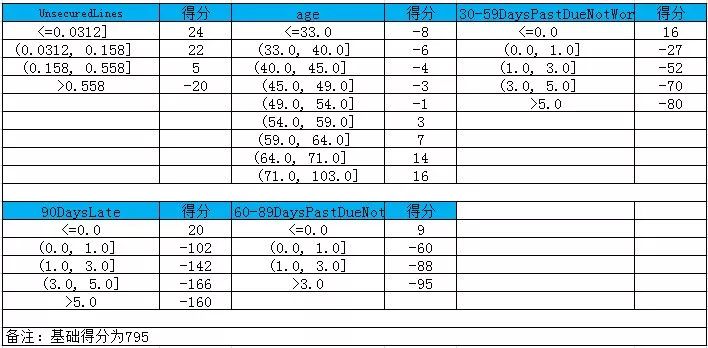
图7-1 各变量的评分标准
#
❽
自动评分系统
根据变量来计算分数,实现如下:
-
#根据变量计算分数
-
def compute_score(series,cut,score):
-
list = []
-
i = 0
-
while i < len(series):
-
value = series[i]
-
j = len(cut) - 2
-
m = len(cut) - 2
-
while j >= 0:
-
if value >= cut[j]:
-
j = -1
-
else:
-
j -= 1
-
m -= 1
-
list.append(score[m])
-
i += 1
-
return list
我们来计算test里面的分数:
-
test1 = pd.read_csv('TestData.csv')
-
test1['BaseScore']=Series(np.zeros(len(test1)))+baseScore
-
test1['x1'] = Series(compute_score(test1['RevolvingUtilizationOfUnsecuredLines'], cutx1, x1))
-
test1['x2'] = Series(compute_score(test1['age'], cutx2, x2))
-
test1['x3'] = Series(compute_score(test1['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, x3))
-
test1['x7'] = Series(compute_score(test1['NumberOfTimes90DaysLate'], cutx7, x7)
-
test1['x9'] = Series(compute_score(test1['NumberOfTime60-89DaysPastDueNotWorse'], cutx9, x9))
-
test1['Score'] = test1['x1'] + test1['x2'] + test1['x3'] + test1['x7'] +test1['x9'] + baseScore
-
test1.to_csv('ScoreData.csv', index=False)
批量计算的部分分结果:
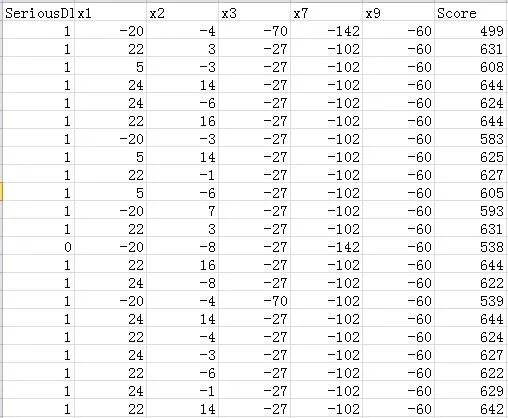
图8-1 批量计算的部分结果
❾
总结以及展望
本文通过对 kaggle 上的 Give Me Some Credit 数据的挖掘分析,结合信用评分卡的建立原理,从数据的预处理、变量选择、建模分析到创建信用评分,创建了一个简单的信用评分系统。
基于 AI 的机器学习评分卡系统可通过把旧数据(某个时间点后,例如2年)剔除掉后再进行自动建模、模型评估、并不断优化特征变量,可以使系统更加强大。
文章链接 | https://zhuanlan.zhihu.com/p/35284849
【Python】利用Python开发信用评分卡就为大家介绍到这里,
《python金融风控评分卡模型和数据分析(加强版)》
更多相关实战案例会定期更新,用于银行培训,论文参考,大家记得收藏课程。