A Ship Detector Applying Principal Component Analysis to the Polarimetric Notch Filter
将主成分分析应用于偏振陷波滤波器的船舶探测器
摘要
近年来,利用极化合成孔径雷达(PolSAR)数据进行舰船探测引起了人们的广泛关注。偏振测量可以提供有关目标散射机制的信息,这有助于区分船只和海杂波。当我们的目标是探测处于恶劣海况的小型船只时,这种增强尤其有价值。这项工作利用了一种称为几何摄动偏振陷波滤波器(GP-PNF)的舰船探测器,旨在提高其性能,尤其是在可获得较少偏振图像(例如,双偏振数据)时。该想法是设计一种新的极化特征向量,其中包含更多的特征,这些特征以允许船只和海杂波之间的分离而闻名。然后,进一步使用主成分分析(PCA)来降低新特征空间的维数。在四个真实的Sentinel-1数据集上进行了实验,以证明所提出的方法的有效性,并将其与其他船舶探测器进行了比较。实验结果分析表明,该算法不仅可以显著减少虚警,而且可以提高目标杂波比(TCR),从而更有效地检测较弱的舰船。
1 Introduction
在过去几十年中,许多国家都高度重视海上监视。除了自动识别系统(AIS)[1],合成孔径雷达(SAR)由于其昼夜成像能力和穿透云层的能力,已广泛用于海上监视。然而,船舶探测仍然是一项具有挑战性的任务,特别是当我们想要探测较小的船舶或海况较高时。海面风或其他海洋现象引起的海洋反向散射也会产生许多错误警报。另一方面,来自船舶的反向散射主要由船体和金属结构上的多次反射组成,对于较小的船舶,其反射相对较弱[2]。因此,能够有效消除虚假警报并同时检测较弱船舶的强大方法在SAR船舶检测中发挥着重要作用。
到目前为止,已经在舰船探测方面做了大量工作,利用了不同的机载和星载SAR系统,如AIRSAR、TerraSAR-X和Radarsat-2[3]。在早期的研究中,大多数方法探索了单极化SAR图像,其中大量使用了恒虚警率(CFAR)检测[4,5]。Eldhuset[6]采用自适应滤波器来检测候选船舶,并进一步利用船舶尾流作为次要指标。这可以为减少错误警报的数量提供额外的信息。Leng等人[7]结合了单通道SAR图像的强度分布和空间分布,以减少误报和检测船舶。基于离散小波变换,Tello等人。 [8]提出了一种利用四个不同子带相乘的新的舰船检测器。 尽管传统的单通道数据可用于在相对平静的海况下探测大型船舶,但使用它们在较高海况下探测小型船舶仍然具有挑战性。
与单极化模式相比,全极化模式可以获得更多的后向散射信息,从而提高目标与海杂波的分辨能力。近年来,已经开发了许多使用四极化SAR(PolSAR)数据的算法。最直接的方法直接利用PolSAR数据作为使用协方差/相干矩阵进行船舶检测的基本特征。除了偏振SPAN(总功率)检测器[9],偏振白化滤波器(PWF)检测器[10]是最常用的船舶检测算法。它使用所有通道以最佳方式减少斑点[11],提供比SPAN更好的性能。然而,PWF检测器可能会漏掉较弱的血管[10]。
一些算法利用统计数据。基于全极化SAR数据,Liu等人[12]将使用高斯分布的恒虚警检测器应用于每个频带。最终结果取决于所有三个独立信道中最高的检测概率。已经提出了新的模型,它们显示出更好的性能。这些统计模型包括Weibull、Gamma、G0和K分布。
或者,可以从协方差矩阵或相干矩阵计算不同的极化分解(PD)方法或参数。其中一些参数可用于区分船只和海杂波。杉本等人利用山口分解来发现船只和海面之间的差异[13]。Wang等人[14]使用不同的PD算法来分析几种类型船舶的散射。在[15]中,对称散射表征方法(SSCM)是Cameron方法[16]的扩展,用于船舶检测。在C波段AIRSAR数据上测试的初步结果证明了该方法的可靠性。Cloude等人[17]利用Cloude–Pottier分解计算的熵和α角成功检测目标。Nunziata等人[18]利用海杂波的反射对称性(RF)特性来检测海上目标。为了找到更稳健的算法,Yang等人[19]开发了一个新的参数来反映两个散射矩阵之间的相似度,并引入了一种通用对比度优化方法,该方法可以有效提高舰船的目标杂波比(TCR)[20]。Marino等人[21]提出了一种利用Huynen分叉进行目标检测的新检测器,该检测器提取了极化目标复杂空间中的目标特征。这在Marino等人提出的一种称为几何扰动偏振陷波滤波器(GP-PNF)的船舶探测器中达到了顶峰。[22]。
总体而言,所有上述方法主要属于“基于像素的”类别,这意味着大多数特征都是通过像素方法提取的,使用单视散射矩阵或多书协方差/相关性矩阵[23]。一些研究人员考虑到目标像素周围的偏振信息,拓宽了这一概念。Wang等人[23]采用超像素模型来推导用于舰船检测的新偏振散射特征。Zhang等人[24,25]使用船舶像素与其周围杂波像素之间的差异来改进船舶检测的TCR。然而,由于计算极化协方差差矩阵(PCDM)和特征值的负担,该算法仍然耗时。
利用当今的技术,四极化SAR数据仅在有限的幅宽下可用[26]。因此,使用具有双极化和更宽波段的SAR数据对于操作目的更为实用[26]。
基于离散小波变换,Tello等人。 [8]提出了一种利用四个不同子带相乘的新的舰船检测器。 在这项工作中,我们利用了欧洲航天局(ESA)的哨兵-1号数据。 哨兵一号于2014年4月由欧空局发射。 它有几种工作模式,可以实现广覆盖的中高分辨率成像[27]。 干涉宽条带(IWS)模式获得了VH/VV(或HH/HV)双极化组合,可以在5m×20m(距离×方位)空间分辨率下提供250km的单视复格式条带。 一些工作已经将Sentinel-1用于船舶探测[28-30],证明Sentinel-1数据非常适合于这项任务。 然而,双极化SAR在探测较弱的船只时存在问题,尤其是在海况较高的情况下。
近年来,主成分分析(PCA)[31]已广泛应用于遥感技术[32]。Ready等人[33]证明,使用PCA可以从有噪声的多光谱数据中显著提高信噪比(SNR)。Eklundh[34]等人发现,使用标准化主成分分析(sPCA),我们可以比非标准化主成份分析(uPCA)更有效地提高SNR。Lee等人[35]使用主成分变换(PCT)来减少PolSAR图像中的斑点。
在上述方法的鼓励下,本文提出了一种改进的GP-PNF方法,以提高船舶的TCR值,特别是在粗糙海况下,对于散射较弱的船舶。四个真实的Sentinel-1 IW数据集被进一步用于测试其性能。
本文的其余部分结构如下。第2节介绍了理论背景。第三节提出了基于GP-PNF和PCA的舰船检测方案。在第4节中,详细介绍了Sentinel-1数据的实验结果和讨论,该数据包括一个平静海况的港口数据集、一个中等/粗糙海况的海港数据集和两个粗糙海况的近海数据集。最后,第5节总结了本文。
2. Theoretical Background
2.1. Theory of Polarimetric SAR Data
散射矩阵[S]可以有效地表示物体的偏振信息。以线性水平和垂直极化为例,[S]可以表示为[36]:
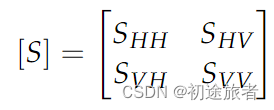
其中,例如,SHV表示水平接收和垂直发射极化信道。当目标是倒数时,其[S]散射矩阵是对称的,即热噪声的SHV=SV Hexcept。对于双极化情况,散射矩阵[S]可以简化为列向量[37]:
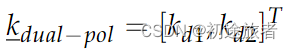
其中kdual−pol表示双pol SAR的散射矢量[38],上标“T”表示矩阵转置。元素kd1和kd2分别表示共极性散射元素(SHH或SVV)和交叉极性散射元件(SHV或SVH)。
为了进一步分析分布式目标的物理信息,我们可以使用散射向量的二阶统计量,例如协方差矩阵[C]或相干矩阵[T]。在本文中,我们选择VH/VV作为双偏振模式。因此,所得协方差矩阵定义为[36]:
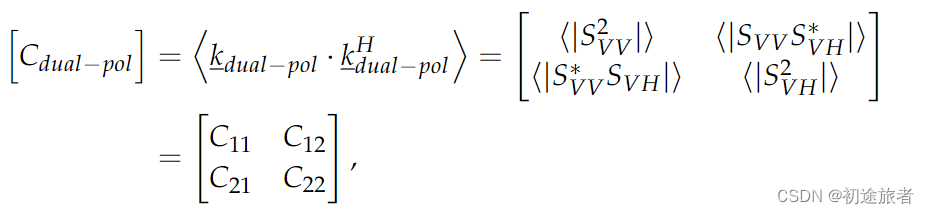
其中上标“H”表示共轭转置,〈·〉表示空间平均,|·|表示幅度,“*”表示复共轭。
2.2. Geometrical Perturbation-Polarimetric Notch Filter (GP-PNF)
GP-PNF由Marino等人提出[38],它是几何扰动滤波器(GPF)[39]的一种改进,在极化空间中用作陷波滤波器。GP-PNF可以通过在协方差矩阵的极化空间中隔离和拒绝海面回波来有效地检测海面上的物体。
在GP-PNF中,首先构建6D部分散射特征向量t,即[40]:
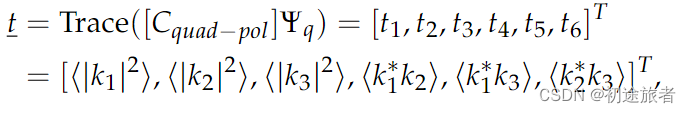
其中Ψq是埃尔米特内积下的一组6×6基矩阵,ki(i=1,2,3)是在单站传感器和互易的情况下从Sinclair散射矩阵[S]导出的散射向量k的元素。考虑到我们将在这项工作中使用双极化数据,利用了双极化特征向量tdual−pol[39]:
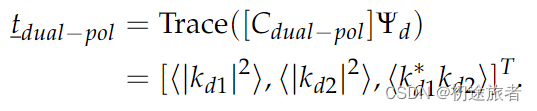
请注意,双极化特征向量只能提供全极化空间的不完全观测[40]。
然后,进一步设计矢量tT来表示部分目标。此外,还获得了稍微扰动tT的伪目标tP(即,稍微修改tT的所有分量)。因此,在一系列数学操作[40]之后,最终的双偏振检测器被定义为:

其中,RedR是一个称为缩减比率的参数,PC和PT分别表示杂波和目标的功率。
总之,如果部分目标在感兴趣的目标上具有强分量,则PT将大于PC,γ将接近1。
2.3. Principal Component Analysis (PCA)
丰富的多维数据集通常允许提取许多特征。在雷达极化数据的情况下,我们可以提取所谓的“极化特征”。然而,这些特征中的一些将是相关的。因此,减少特征数量,但仍保留原始数据集中的有用信息是有帮助的[31]。主成分分析(PCA)是减少特征维数的有效工具[41]。其目标是找到一个子空间,其中包含了先前特征空间中的大部分方差[42]。
假设我们的信号X由作为n个随机变量的向量X的n个测量值组成,并且我们希望将维数从n减小到m,其中m小于n。首先,我们让信号X具有协方差矩阵[∑],分别具有[P]和[∧]特征向量和特征值矩阵,即[43]:[Λ] = [P]T [Σ][P].
可以证明,与m个正交基向量的所有其他可能选择相比,对应于m个最大特征值的[∑]的m(m≤n)特征向量集(这里称为Am)将使均方重建误差最小化[43]。然后,PCA信号Y可以被给出为:Y = [X]Am,
其中[X]是原始数据矩阵,Am=[a1,a2,…,Am]T。
3. Methodology
本节的第一部分分析了所提出方法中使用的一些偏振特征。在第二部分中,将创建新的偏振散射矢量。最后,我们将使用GP-PNF框架来设计船舶探测器。
3.1. Analysis of Polarimetric Features
极化特征可分为两类:(1)直接从PolSAR数据中选择,如散射矩阵[S]和协方差矩阵[C];(2) 在操纵散射或协方差矩阵的元素之后选择。
总体强度是船舶检测中非常重要的特征。其计算为协方差矩阵的对角元素之和[Cdual−pol][9]:SPAN = C11 + C22.
交叉极化信道中的海洋反向散射通常比共极化信道中弱。这是因为海洋散射通常可以使用布拉格散射来建模[44]。另一方面,船舶的主要散射是由高反射表面和角落的反射产生的,这些反射通常会被周围海洋的反射增强。由于这些多重反射具有角的随机取向,我们期望有一个强的交叉极化通道。因此,利用共极化信道(SHH或SVV)和交叉极化信道(SH V或SV H)的特征可以帮助我们检测船舶[45]。与[8]中的乘积运算不同,Hannevik[46,47]通过将两个通道的振幅相乘并除以一个常数(这里,我们称其为“MTC”检测器)开发了一种检测器:
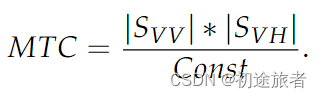
与SPAN类似,这种度量在恶劣的海洋状态下效果较差。因此,仅使用MTC将产生错误警报。然而,MTC对于高入射角是有效的;因此,我们将其添加到极化特征向量中。我们在本文中设置Const=1,因为它只是一个比例参数。
极化度(DP)也可以提供重要信息,因为海洋被认为具有高极化度,而船舶具有较低的极化度。极化程度可以使用斯托克斯参数[48]进行评估:
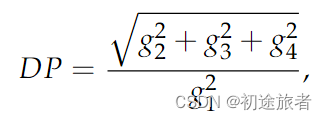
其中斯托克斯参数由[49]给出:
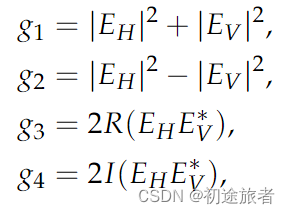
其中E是在下标极化中接收到的复电场,R(·)和I(·)表示复电场的实部和虚部。 图齐等人。 [50]利用四极化数据证明了对所有可能的DPS进行优化是有用的。 同样,Shirvany等人。 并用双波尔SAR数据证明了DOD=1-DP的去极化度对舰船探测的有效性[49]。 同时,考虑到DOD与发射极化无关,适合于星上实现[49],我们选择它作为最后一个扩展极化特征向量。
总之,不同的特征有其各自的优点和缺点。为了解决不同方法的缺点,提高GP-PNF的性能,在GP-PNF特征向量中加入了新的特征。
3.2. Constructions of Scattering Vectors
我们形成如下偏振散射矢量(SVN),如表1所示:
•SV1:它是GP-PNF的原始特征向量。我们认为这些特征是直接从协方差矩阵[C]中选择的PolSAR数据的基本表示
•SV2:在本文中,我们使用三个额外的极化特征(即SPAN、MTC和DoD)扩展了3D SV1矢量。它们都已成功用于船舶检测,并可在GP-PNF框架内有效补充船舶极化信息。
•SV1PCA和SV2PCA:它们是由PCA产生的基础的前三个轴导出的特征向量。SV1PCA具有与原始SV1相同的维度,但用于表示它的基础不同,它被转移到数据集群的中心。SV2PCA认为与6D SV2向量相比,维数从6减少到3。

3.3. The Proposed Ship Detection Method
如图1所示,第一步是构建包含更多极化特征的更大特征向量t′:
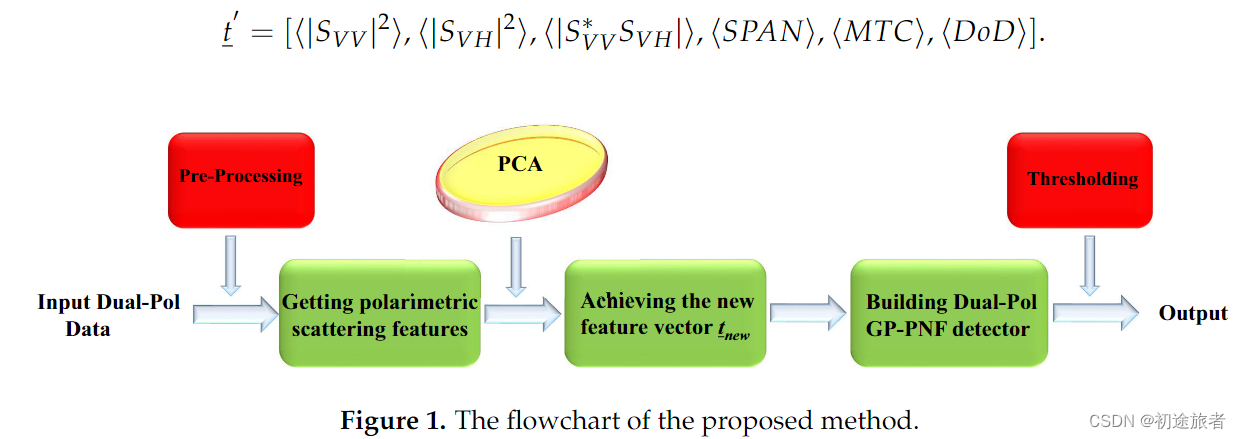
然后,使用PCA来改变基础并降低t′的维数。这里,我们只保留最终PCA基础的前三个轴,并调用生成的向量tnew:
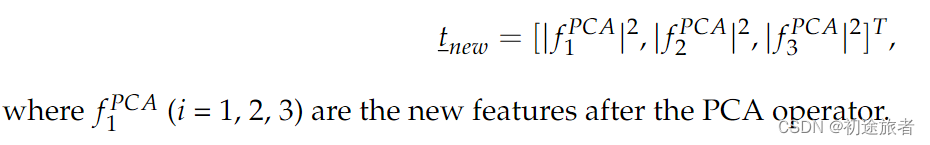
由于我们正在评估包含目标的二阶统计量的特征向量的协方差矩阵,因此我们有效地利用了更高阶统计量。未来将开展进一步的工作,以了解考虑此应用的高阶统计的重要性。
最后,检测器的最终表达式构建为:
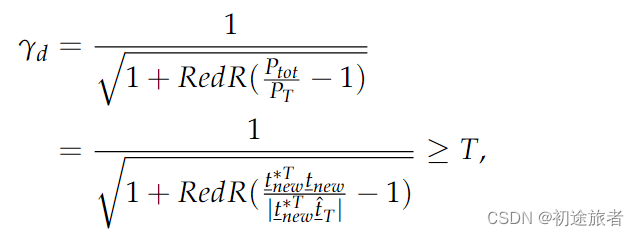
其中,Ptot是tnew的幂,⑪tT是部分目标向量tT[41]的归一化版本,“T”是阈值。这里,我们还给出了算法1所示的所提出方法的伪代码。

4. Results and Discussion
为了证明所提出的方法在PolSAR船舶检测中的有效性,我们在四个免费可用的Sentinel-1数据集上进行了实验。三种常规检测算法,即VH(即HV)检测器[46]、MTC检测器[47]、去极化度(DoD)检测器[49]和反射对称(RF)检测器[18]用于比较。另一方面,还采用了一系列几何扰动偏振陷波滤波器(GP-PNF)方法(此处称为“PNFX”)[37–39]进行比较。因此,总共使用了八种算法:
•VH:VH的振幅,
•MTC:振幅VV和VH的乘积,
•DoD:去极化程度,
•RS:反射对称性,
•PNF3D:使用SV1特征向量(原始),
•PNF6D:使用SV 2特征向量(建议),
•PNF3DPCA:使用SV1PCA特征向量(提议),
•PNF6DPCA:使用SV2PCA特征向量(建议)。。
所有实验主要在具有2.60 GHz i7-6770HQ CPU和12 GB内存的计算机上进行。
4.1. Datasets
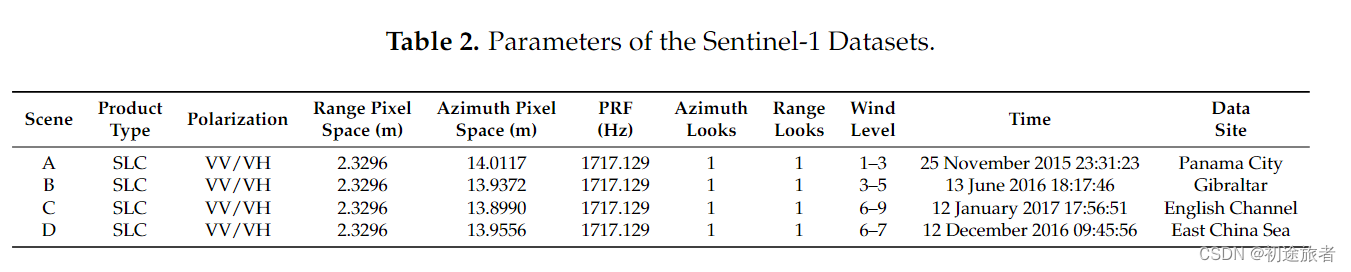
本文采用四个Sentinel-1IW双pol场景来评估所提出的方法。第一个场景于2015年11月25日在巴拿马城港口拍摄,当时巴拿马城处于蛤海状态。其VH振幅图像和从Google Earth获得的光学图像如图2所示。为了避免陆地的影响,从港口进一步选择了一个名为“A”的分区作为我们的实验数据集(见图2c)。图2b中的绿色方框(550×990像素)突出显示了这一点。图2b中随机选择红色区域(400×400)作为海杂波的样本区域。第二幕于2016年6月13日在直布罗陀港拍摄。光学和VH振幅图像如图2d,e所示。类似地,我们选择一个名为“B”的分区作为实验数据集(见图2f),图2e中的绿框(740×950)也突出显示了这一点。海杂波的样本区域仍然是随机选择的,并由图2e中的红色方框(400×400)表示。请注意,B的海况比A更粗糙。第三个场景于2017年1月12日在英吉利海峡拍摄,其相应的光学图像如图2g所示。数据集“C”(3597×5273像素)的VH振幅图像如图2h所示。与A和B相比,C的海况最为恶劣。最后一个数据集“D”(1101×781像素)于2016年12月12日在东海获得,那里的海洋状态与C一样粗糙。其相关光学和VH振幅图像如图2i,j所示。需要指出的是,海洋数据,即风力等级,是从英国气象局[51]和CMA国家气象中心[52]收集的。表2列出了四个数据集的所有采集参数。
为了评估船舶探测性能,应提供地面真实数据,其中标记船舶位置。然而,我们没有与四个数据集相对应的地面实况数据,特别是AIS信息。相反,本文主要通过目视检查确定船舶的位置。
4.2. Evaluation Criteria
为了评估不同方法的检测性能,我们需要一些具有图像中船舶位置的验证数据集。在这项工作中,我们通过对SAR图像的视觉检查来确定真实船舶的位置。检测结果都以二进制格式表示,其中白色表示船只,黑色表示海杂波。手动选择每个检测器的阈值,以获得具有最高可能检测概率Pd和最低可能误报概率Pf的最佳检测掩码。这是为了模拟能够找到最佳阈值的完美统计方法。
以前的方法仍然需要选择可能不是完全最优的阈值。为了避免在选择阈值时出现任何可能的错误,我们进行了一些独立于阈值选择的定量分析。我们采用接收操作特性(ROC)曲线,这是一个曲线图,显示了阈值变化时检测概率与错误报警概率的关系。概率定义为:

其中Ndt是检测到的目标像素的数量,Ntp表示所有目标像素的数目,Nf p表示误报像素的数目并且Ncp表示海杂波像素的数目。


图2:四个数据集。(a) 第一场景的光学图像;(b) 第一场景的VH图像;(c) 数据集A的VH图像(放大(b)的绿色框);(d) 第二场景的光学图像;(e) 第二场景的VH图像;(f) 数据集B的VH图像(放大(e)的绿色框);(g) 第三场景的光学图像;(h) 数据集C的VH图像;(i) 第四场景的光学图像;(j) 数据集D的VH图像。橙色圆圈表示船只。(g,i)中的黄色图标表示(h,j)的位置。
此外,我们使用目标杂波比(TCR)作为检测性能的另一个指标。TCR越高,目标和杂波之间的分离越好,因此检测性能越好。TCR以dB为单位评估为:
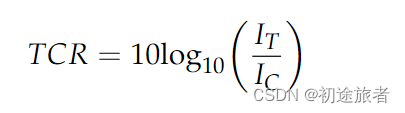
其中,IT和IC分别表示目标和杂波的目标功率PT的平方值。通过识别图像中船舶的几何中心并对明亮像素的PT周围值进行平均来计算IT。对于IC,我们随机选择一个海域(400×400)作为海杂波的样本区域,并对160000像素的PT进行平均。这是因为PT的平方与VH的强度具有相同的维度,因此在检测器之间提供了公平的比较。
4.3. Results and Discussions on the First Sentinel-1 Dataset
图2c显示了数据集A的VH图像,其中包括25艘真实船舶。这里,我们使用橙色圆圈来突出显示它们。请注意,为了在所有PNFX算法中进行公平比较,我们保持窗口大小的参数相同:WinTrain=75,WinTest=7。此外,除VH和RS探测器外,用于其他探测器的平均窗口大小为3×3。选择这些参数以产生特定算法的最佳性能。
事实上,a的海面是这四个数据集中最平静的。由于所提出方法的主要关注点是在粗糙海况下的检测,因此我们简要报告了A的检测结果,作为比较,以更好地理解粗糙条件下的改进。
总之,我们可以发现VHfilter、MTC和所有PNFX方法的结果似乎都非常好。VHfilter和MTC如图3b,c所示。他们检测到所有25艘船,没有误报。这意味着,经过滤波后,VH信道的幅度信息可能足以在海况平静时区分船舶和海杂波。与图3b相比,图3a所示的VH检测器的结果也证明了滤波的有效性。图3d显示了国防部没有检测到船只和一些错误警报的结果。RS结果如图3e所示。显然,虽然检测到的船只的结构是可见的,但并不是所有的船只像素都被检测到。从图3f–i中,我们可以看到一系列PNFX检测器(即PNF3D、PNF3DPCA、PNF6D和PNF6DPCA)的结果相似。他们检测到所有船只,没有误报。这意味着在平静海况下仅使用PNF(SV1)的原始模型就足以检测船舶,因此PCA算子是不必要的。
综上所述,当海况平静时,许多传统方法能够有效地检测船舶,而所提出的算法可能不具有显著优势。
4.4. Results and Discussions on the Second Sentinel-1 Dataset
数据集B的VH图像如图2e所示,其中包括19艘目视识别的船舶。为了更清晰,我们还用橙色圆圈标记所有真实船只,并使用橙色虚线圆圈表示三艘船S1、S2和S3,这三艘船的后向散射要弱得多。表3顶部显示了用于其他检测器的平均窗口大小。


图3。A.(A)VH上不同方法的船舶检测结果;(b) VH过滤器;(c) MTC;(d) 国防部;(e) RS;(f) PNF3D;(g) PNF3DPCA;(h) PNF6D;(i) pnf6主成分分析。

图4给出了所有检测器的结果。 红色圆圈表示错过的船只,黄色虚线圆圈表示虚假警报。 国防部的探测面具显示被探测到的船只很少。 这是因为海杂波很强,船只往往有一个低的DOD值。 为了保持较低的PF,我们必须设置一个非常高的阈值; 因此,在这个数据集中,使用DOD几乎不能检测到任何东西,如图4d所示。 以S1为例,图5表明其DOD值并不比海杂波的DOD值高很多。 使用四极化数据的DP优化可以改善最终的检测掩模。


图4。B.(a)VH上不同方法的船舶检测结果;(b) VH过滤器;(c) MTC;(d) 国防部;(e) RS;(f) PNF3D;(g) PNF3DPCA;(h) PNF6D;(i) pnf6主成分分析。红色圆圈表示失踪船只。黄色虚线圆圈表示错误警报。
如前所述,与海面相比,许多船舶在VH信道中的反向散射更强。同样,图4b的结果表明,与图4a相比,滤波后的交叉极化信道可以使船只的轮廓更加清晰,并有助于检测较弱的船只。图4c所示的MTC结果显示出与VH相似的性能。
图4e显示了RS的结果。尽管许多较大的船只被有效地检测到,但由于RS值较低,所有较弱的船只仍然下落不明。如图6所示,我们可以观察到S1与其周围海杂波像素之间的RS值差异很小。
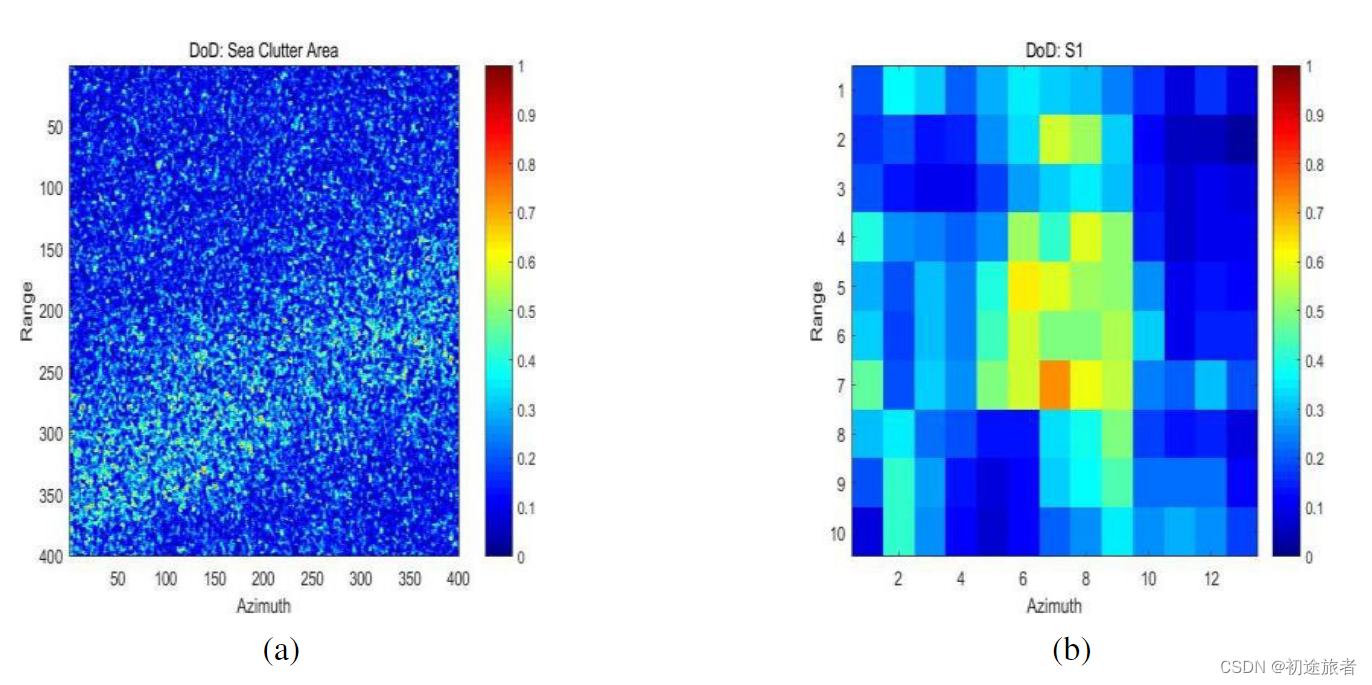
图5.DOD值。(A)海杂波样本面积;(B)s1。请注意,颜色栏的单位已标准化。
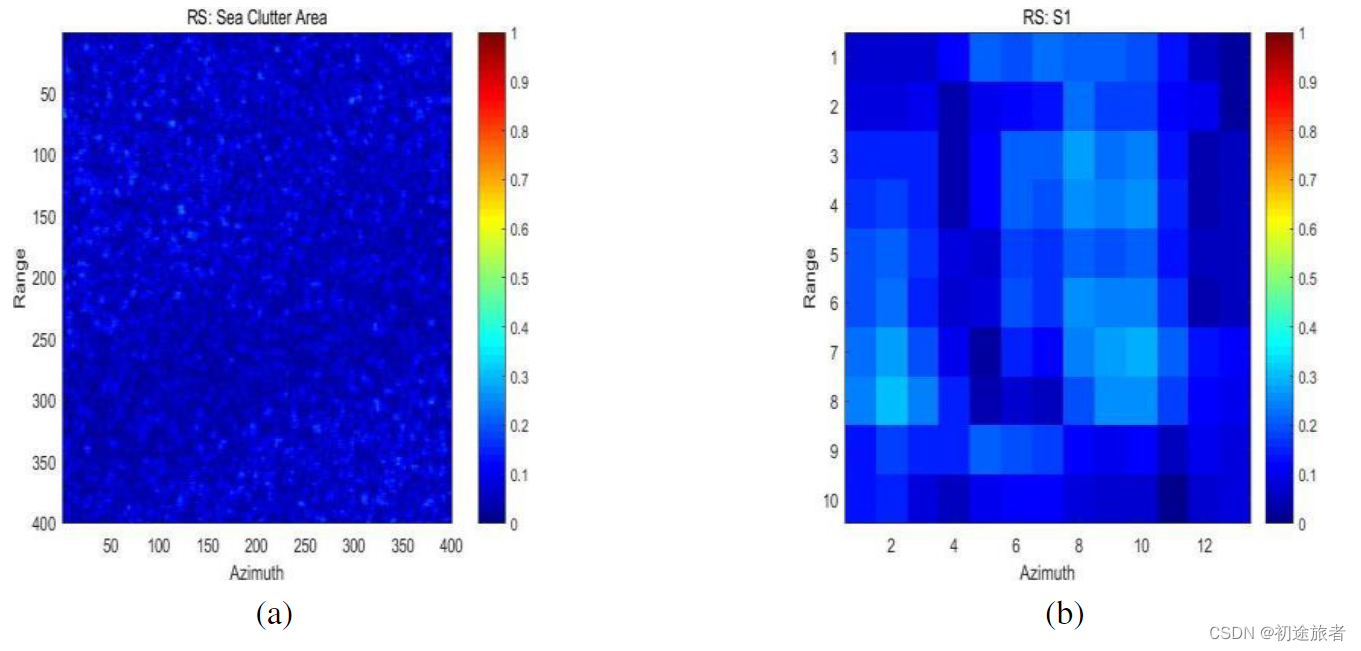
图6.RS值。(A)海杂波样本面积;(B)s1。请注意,颜色栏的单位已标准化。
关于一系列PNFX方法,图4f-i描述了它们的结果。为了公平地比较所有PNFX算法,我们还保持它们的窗口大小参数相同:WinTrain=75,WinTest=7。通过直观的比较,所有的PNFX方法都有很好的结果,因为所有较弱的船只都被检测到了。
这里,我们仍然选择S1作为示例。图7显示了PNFX算法的PT值,这是PNFX检测器的关键指标。与3D矢量相比,6D矢量的S1的PT值更高。这是因为添加功能可以帮助我们增加6D矢量的总功率,这也会增加一些杂波区域的PT。
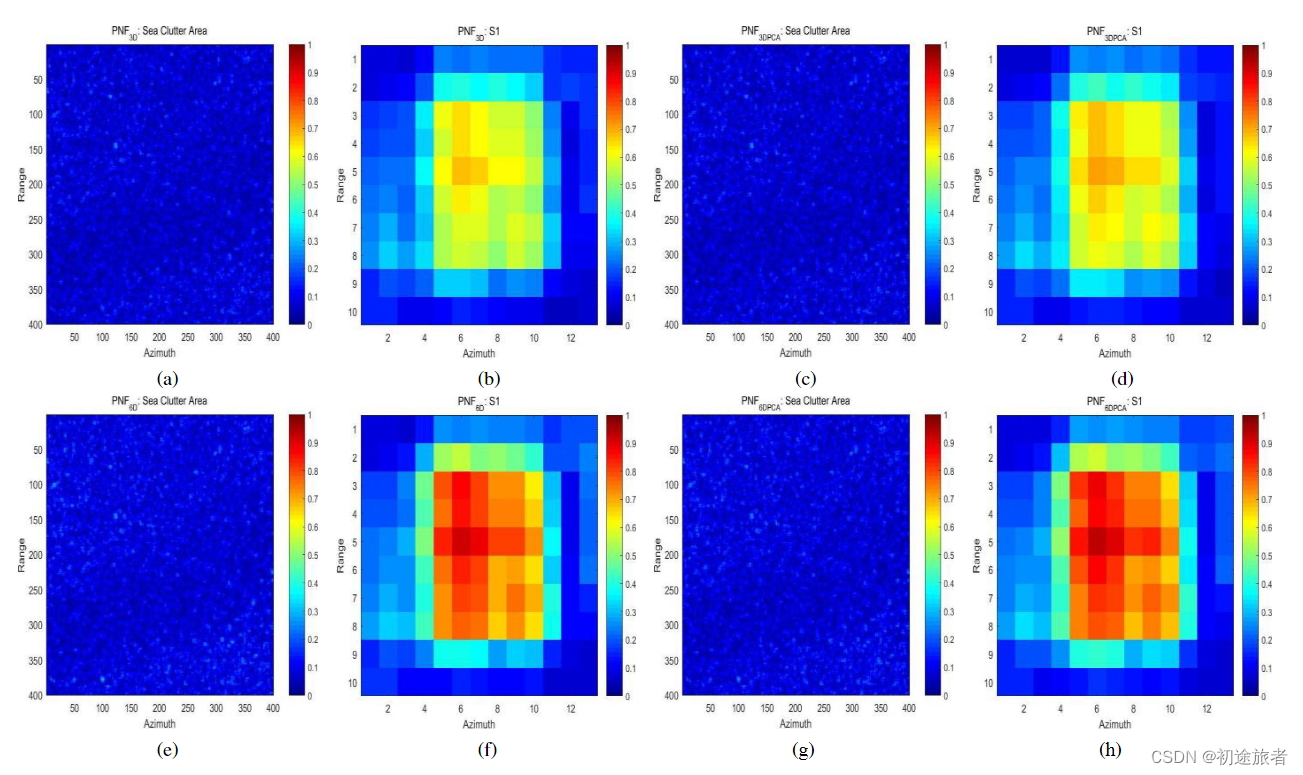
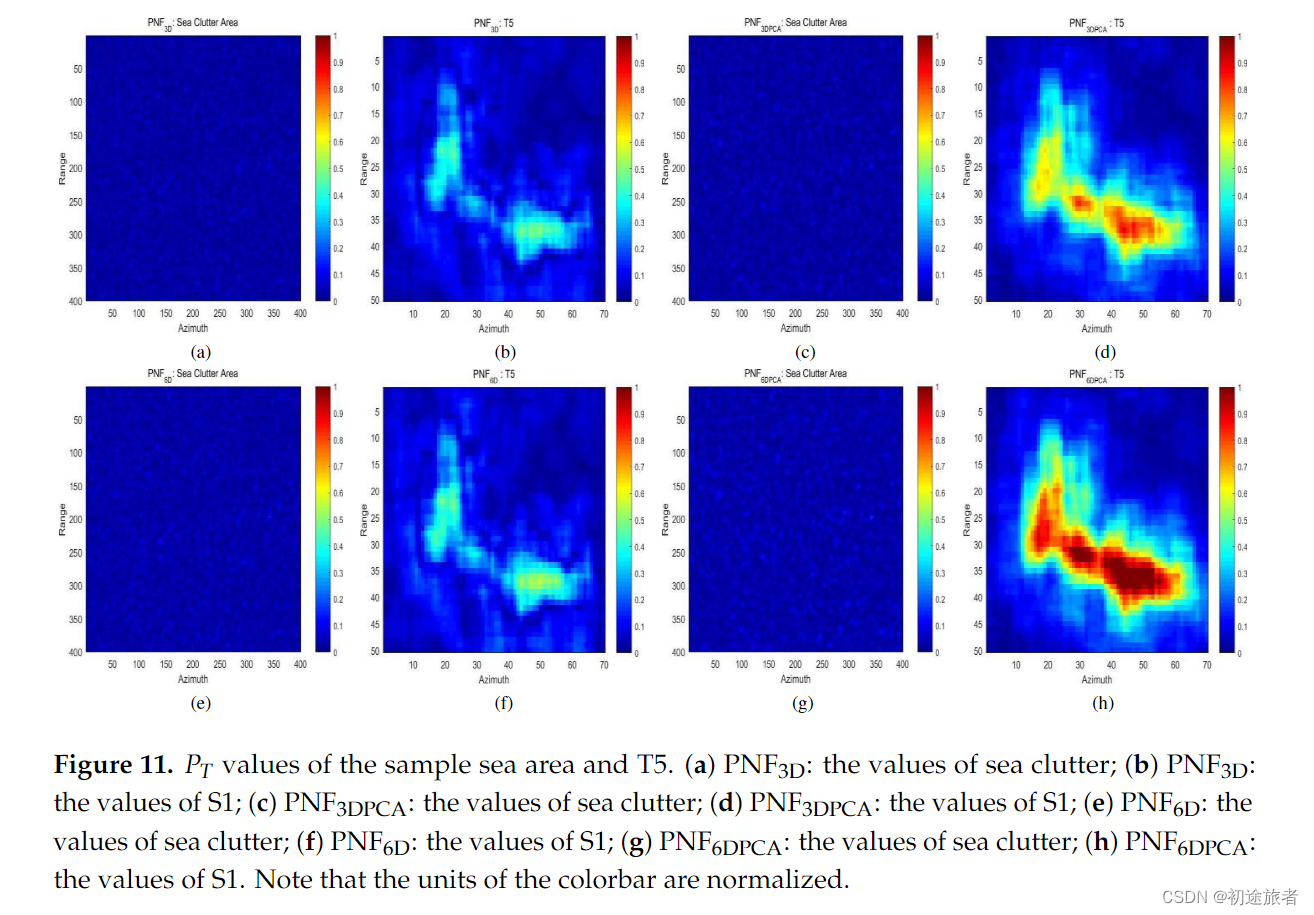
图7.样本海域和S1的PT值。(A)PNF3D:海杂波数值;(B)PNF3D:S1值;©PNF3DPCA:海杂波数值;(D)PNF3DPCA:S1值;(E)PNF6D:海杂波数值;(F)PNF6D:S1值;(G)PNF6DPCA:海杂波数值;(H)PNF6DPCA:S1值。请注意,颜色栏的单位已标准化。
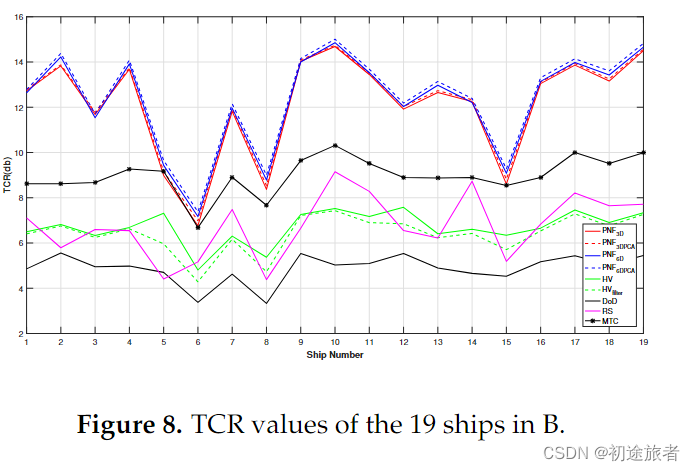
为了更好地了解检测性能是否有所提高,我们在表3中列出了S1、S2、S3和S4(较大的船舶)的TCR值。如表3所示,PNF6DPCA的TCR值最高。这意味着,通过设置适当的阈值,可以更容易地检测到船舶像素。比较PNF3D和PNF3DPCA或PNF6D和PNF6DPCA,我们可以发现使用PCA可以进一步提高TCR。例如,PNF3D的S1的TCR提高了0.11分贝,PNF6D的TCR提高了0.18分贝。主元分析设置特征向量的基础,使其与海杂波最多出现或较少出现的轴对齐。此外,它将轴的中心移动到分布的中间,从而在目标和杂波维度之间实现更好的角度分离。如图8所示,我们可以观察到,PNF6DPCA提高了每艘船的TCR值。此外,这19艘船舶的平均TCR值也列在表3(斜体)的底部。与PNF3D相比,PNF6DPCA的TCR平均提高了0.37dB.而对于一些较弱的舰船,如S1,其增强幅度更大,为0.63dB。
这里,为了更好地了解PNFX探测器,我们放大了图9c中它们的ROC曲线。我们可以发现PNF6DPCA具有最好的性能。在这些Pf值范围内,Pd平均比PNF3D高0.014。
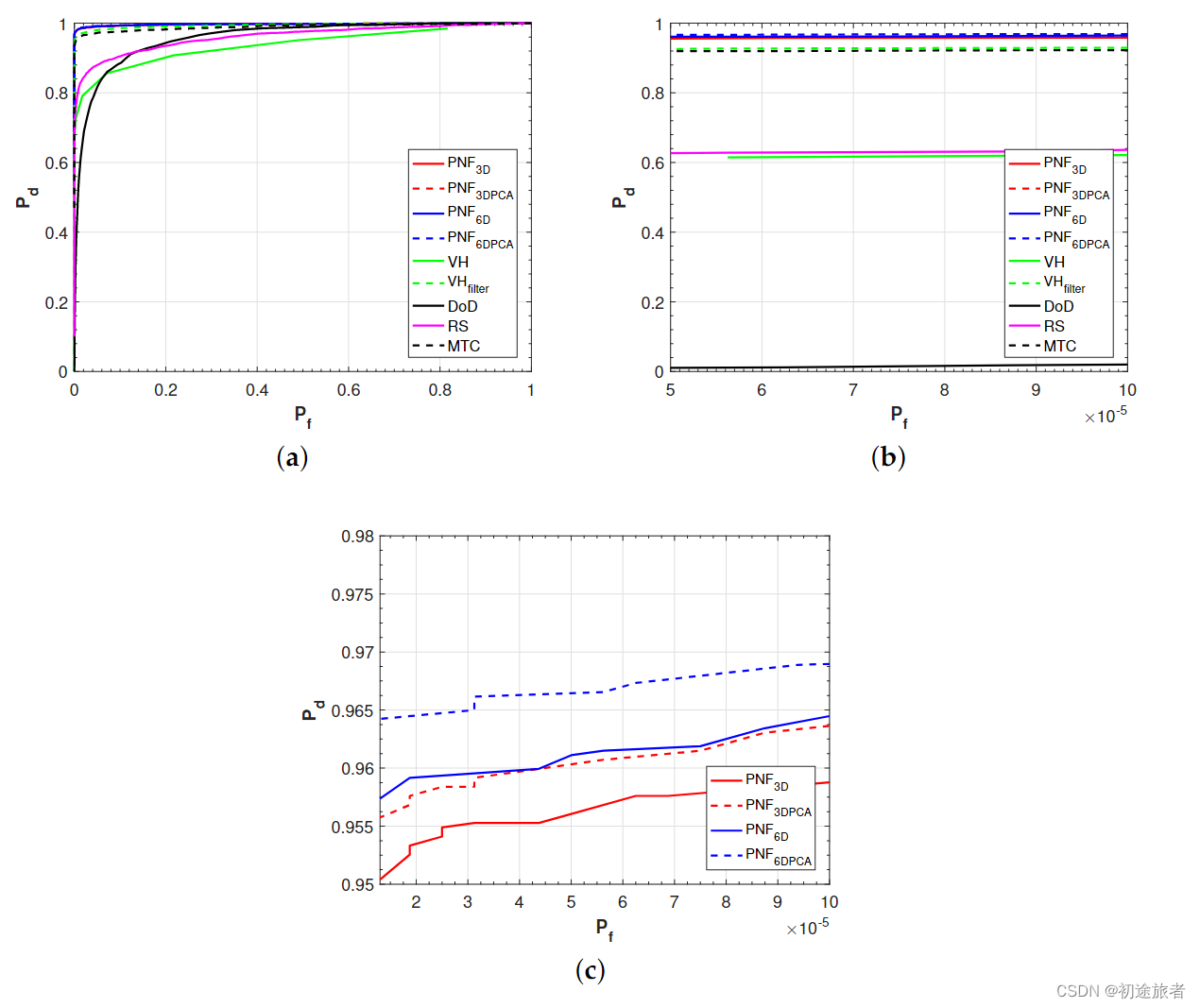
图9.ROC曲线。(A)ROC曲线(PF属于[0,1]);(B)放大PF([0,10−4]);©放大PNFX方法的ROC曲线。
图9显示了这些探测器的ROC曲线,可以进行不受特定阈值影响的公平比较。如图9a所示,我们可以发现,在这九个探测器中,PNFX探测器的性能最好。放大PF小于10−4的ROC曲线,MTC曲线接近VHFilter曲线。
4.5. Results and Discussions on the Third Sentinel-1 Dataset
图2描绘了包含24艘船的第三个数据集C,其大小为3597×5273个像素,具有更大的海域。根据天气报告[52],我们知道与A和B相比,它有更强的风级(6-9级的Beaufort尺度)。我们选择这个数据集来验证在海况非常恶劣的情况下所提方法的有效性。
与图4a相比,我们还可以发现C级船舶在VH通道中看起来不那么明亮,这是因为海杂波更强。图10a显示了VH探测器的结果,我们可以在其中发现一些船只失踪。VHFilter能够检测到较小的船舶,但仍能检测到一个错误警报(图10b)。MTC的结果也如图10c所示,其中有一些丢失的船舶和错误警报。看来国防部(图10d)可以检测到很少的船只,但也可以检测到许多错误的警报。类似地,图10e显示了RS的结果,它错过了一些船只,并且几乎没有错误警报。


图10.不同方法在C.(A)VH;(B)VHFilter;©MTC;(D)DoD;(E)RS;(F)PNF3D;(G)PNF3DPCA;(H)PNF6D;(I)PNF6DPCA上的不同船舶检测结果。红色圆圈表示失踪船只。黄色虚线圆圈表示错误警报。
图10f-i显示了PNFX方法的结果,其中我们看不到错误警报。可以看出,这四种方法都取得了很好的效果,能够有效地检测出全部24艘真实船只。然而,PNF3DPCA和PNF6DPCA检测到的船只要清晰得多。注意,为了公平地比较所有PNFX算法,我们在这里仍然使它们具有相同的参数:WinTrain=75,WinTest=7。
以T5船为例,图11给出了T5的PT值。我们可以发现PNF6DPCA具有最大的值。此外,T5的像素是最亮、最完整的。表4还列出了这24艘船的所有TCR值。PNF6DPCA探测器的TCR值提高幅度最大。与PNF3D相比,∆的TCR值为2.50分贝,高于B值(0.37分贝)。这说明了在海况非常高的情况下,PNF6DPCA是如何最有效地提高船舶的TCR值的。
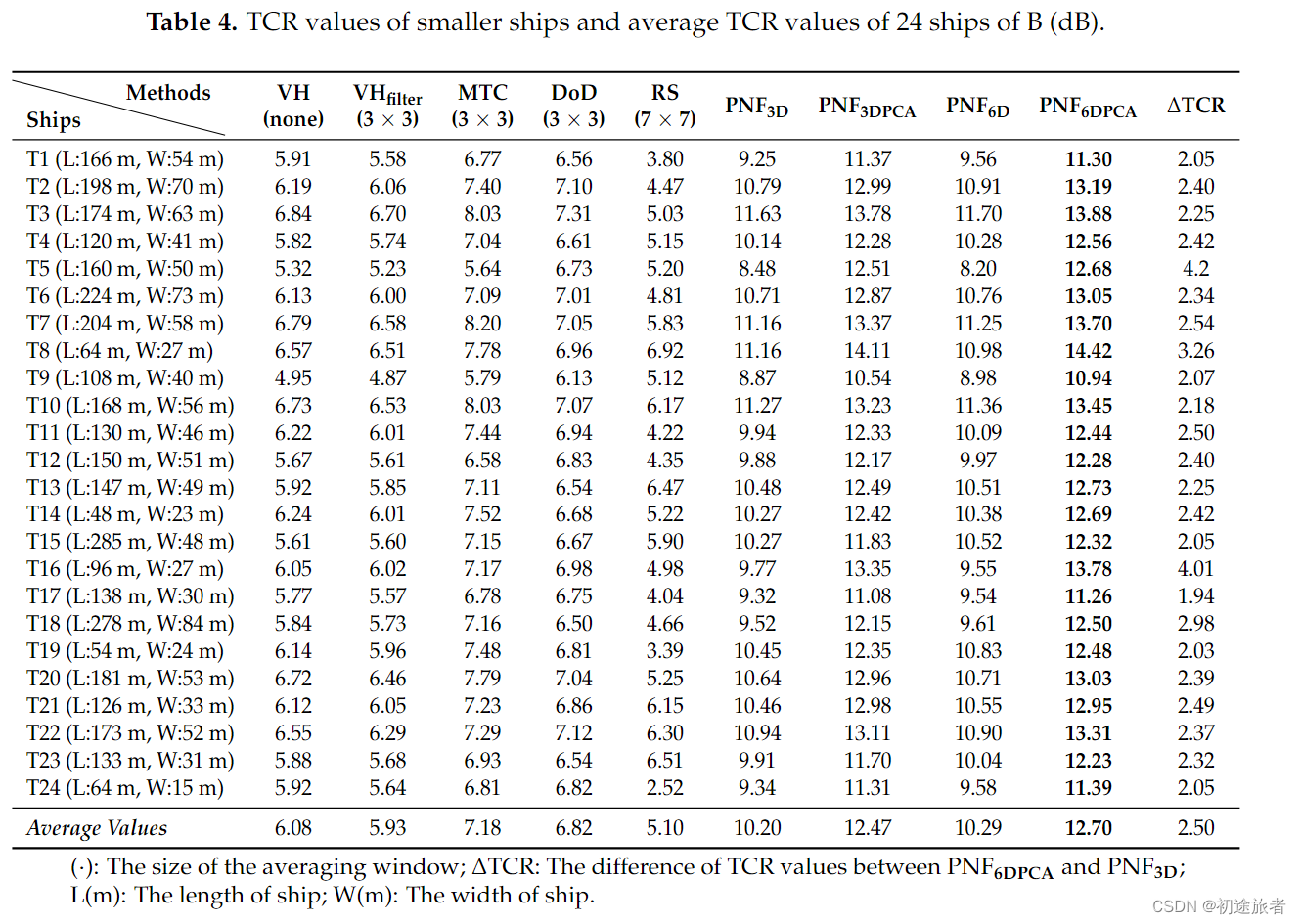
有趣的是,我们注意到与PNF3D相比,PNF6D只提高了大约0.09dB的平均TCR。 这低于数据集B(0.19dB)。 由此可以推断,在波涛汹涌的海况中,改进主要来自于PCA方法,而不是在向量中包含更多的特征。 PNF3DPCA的TCR值分别为0.11dB和2.27dB。 PNF6DPCA的ΔTCR值分别为0.37dB和2.5dB。
我们还在图12中给出了这些检测器的ROC曲线。我们可以看到,所有的PNFX检测器都比其他算法具有更好的性能。放大Pf小于5×10−4的ROC曲线,当Pf小于10−5时,VHFilter检测器的性能是所有传统算法中最好的(图12b)。当海况较大时,PNF3DPCA和PNF6DPCA的曲线比PNF3D和PNF6D有更明显的改善(图12c)。当Pf值在10−5时,PNF6DPCA的PD值接近0.995。我们可以观察到PNF6D的曲线低于PNF3D的曲线。这再次证实,在波涛汹涌的海况下,最大的好处来自于主成分分析方法,而不是添加可能相互强烈关联的额外特征。
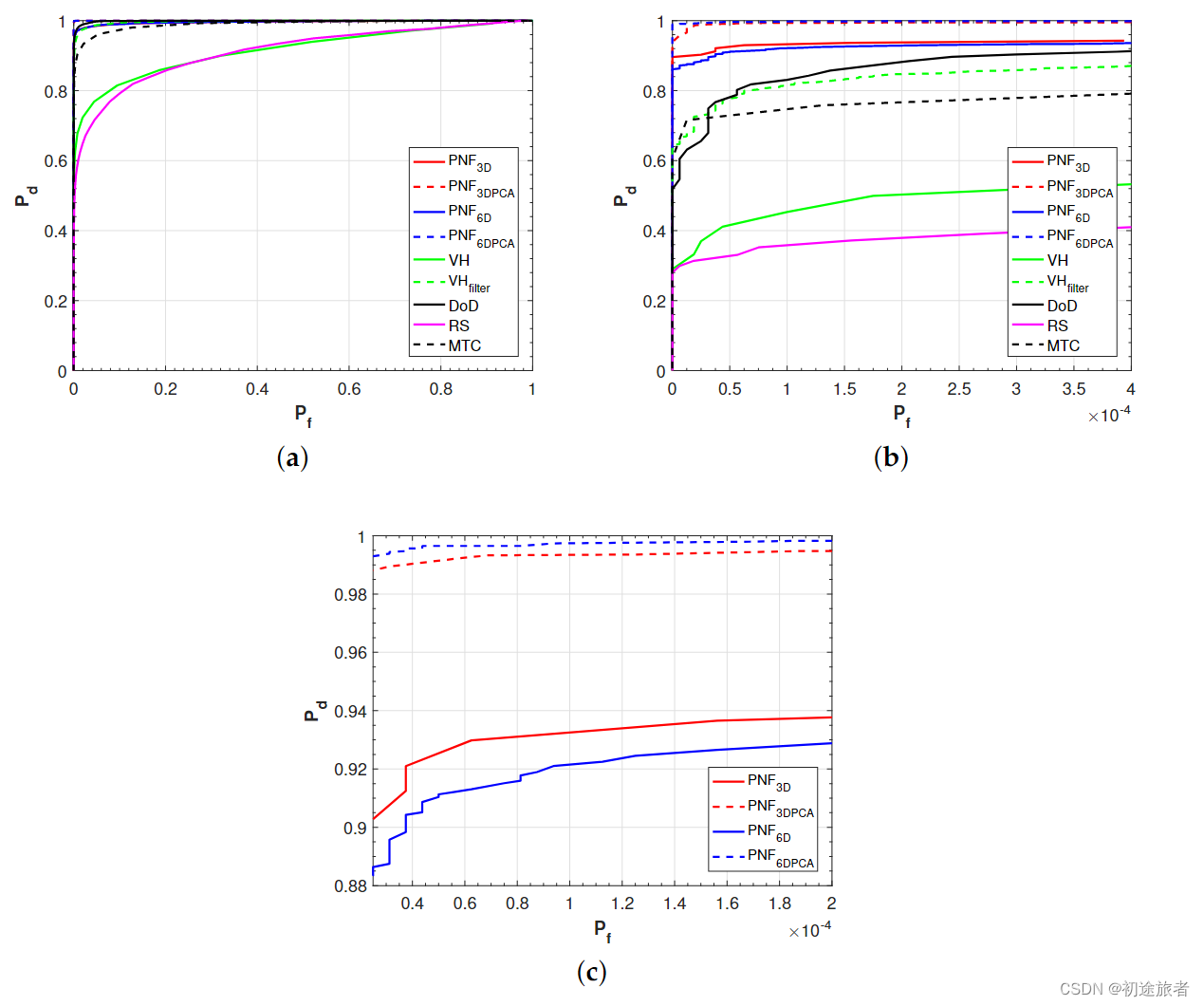
图12.ROC曲线。(A)ROC曲线(PF属于[0,1]);(B)放大PF([5×10−5,10−4]);©放大PNFX方法的ROC曲线。
4.6. Results and Discussions on the Fourth Sentinel-1 Dataset
第四个数据集D(1101×781像素),如图2J所示,由37艘真实船只组成。除了这一场景中存在大风(波福尺度6-7级)[52]外,数据集D还包括更多较小的船只,由于东中国海渔业发达,这些船只可能是小型渔船。因此,它被选为这里的一个具有挑战性的场景。通过图2J中的目视检查,我们可以进一步发现,这些较小的船只大多被淹没在背景杂乱中。
为了节省篇幅,这里我们只给出不同方法的结果。图13a显示了VH的结果,它错过了9艘较小的船只,并同时检测到一些错误警报。与VH相比,VHFilter(图13b)检测到更多较小的船舶,但也检测到一个错误警报。这再次证明了在海况较高的情况下,滤波有助于舰船检测。图13c描述了MTC的结果。我们可以发现,更多的较小船只被遗漏,还检测到两个错误警报。DoD的结果似乎是最差的,如图13d所示。它包括许多失踪的船只和错误的警报。图13E中所示的RS的结果也反映出,当背景杂波很强时,RS对于检测较小的船只可能不是很有用。


基于相同的参数(wintrain=75,wintest=7),我们还在图13F-I中显示了PNFX方法的结果。 观察图13F,我们可以发现PNF3D检测到了大部分的船只,但仍然漏掉了两艘较小的船只,并检测到了两个假警报。 与图13F相比,我们可以看到PNF3DPCA(图13G)显示出比PNF3D更好的检测船只的性能,因为没有检测到较小的船只和假警报。 这进一步说明采用PCA的有效性。 图13H描述了PNF6D的结果。 即使PNF6D没有检测到假警报,它仍然错过了一艘较小的船。 图13i给出了PNF6DPCA的结果。 所有37个目标都被正确地检测到,没有假警报。
在这个充满挑战的场景中,PNF6DPCA更清楚地展示了提高检测性能的能力,特别是对于较小的船舶。
5. Conclusions
在GP-PNF和PCA的框架下,我们探索了两种类型的船舶检测算法。一种考虑只是扩展GP-PNF使用的极化特征向量中的特征数目。另一种方法是在应用GP-PNF之前对特征向量进行主成分分析。新算法在四个真实的哨兵-1数据集上进行了测试。仿真结果验证了所提方法的有效性,特别是在海况较大的情况下。这项工作的主要贡献如下:
在双极GP-PNF方法的原始特征向量中加入更多的极化特征,能够更有效地反映舰船和杂波的差异。因此,特征向量从三维扩展到六维。
在6D向量的基础上,我们使用主成分分析方法将空间再次降维到三维。在四个真实的Sentinel-1数据集上测试的实验证实了PCA操作的有效性。特别是,当海况较高时,经过主成分分析后,可以更有效地检测到较小的船舶。同时,我们还证明了当出现高海况时,仅在特征向量中加入极化特征可能并不有效。
此外,我们还测试了其他检测器的性能,显示了PNFX算法更好的性能,其中PNF6DPCA在海平面较高的情况下性能最好。作为未来的工作,应该分析更多来自其他传感器的数据集,并特别关注四偏振数据。
作者供稿:T.Z.和A.M.构思并执行了这些实验。A.M.和H.X.监督了这项研究,并为文章的组织做出了贡献。T.Z.起草了手稿,所有作者修改并批准了手稿的最终版本。
表彰:本工作得到了中国国家自然科学基金(批准号:61375008,61331015)和欧空局/国家空间研究中心“龙-4”计划(批准号:32235)的部分资助。作者要感谢欧空局的哨兵科学数据中心通过哥白尼任务提供了哨兵1号合成孔径雷达数据。
利益冲突:作者声明没有利益冲突。