一、查询后继节点
后继节点:中序遍历时,某个节点的后一个节点即是该节点的后继节点。
规定二叉树的结构如下:
public static class Node {
public int value;
public Node left;
public Node right;
// 父节点
public Node parent;
public Node (int v) {
value = v;
}
}
如何快速的找到某个节点的后继节点
1、思路
1、按照后继节点的定义来查找某个节点的后继节点
即按中序遍历此二叉树,再查找指定节点的后继节点。
时间复杂度是O(N)
。显然此方法不是最优解。
2、根据二叉树的结构,以及多的这个parent指针来查找
(1)指定节点X有右树,则X的后继节点就是X右树上最左的孩子。根据后继节点的定义得出的。
(2)X无右树,则根据parent指针往上找,直到找到某个节点是它父节点Y的左孩子为止,则Y就是X的后继节点;如果一直往上都没有找到某个节点是它父节点的左孩子,则该节点是最右的孩子,无后继节点。
Why:因为X是Y左树上的最右孩子,按照中序遍历的顺序,遍历完X就是Y了。

时间复杂度是O(K)
(K是指定节点到后继节点的最短节点数)
很显然第二种方法更优。
2、代码
/**
* 查找后继节点
*
* @author Java和算法学习:周一
*/
public static Node successorNode(Node node) {
if (node == null) {
return null;
}
// 有右孩子
if (node.right != null) {
// 找到右树上最左的孩子
return getMaxLeft(node.right);
} else {
// 无右孩子
// 根据parent指针往上找
Node parent = node.parent;
// 没有找到最顶上,且当前节点是父节点的右孩子则一直往上找
while (parent != null && parent.right == node) {
node = parent;
parent = node.parent;
}
// parent包含两种情况
// 1)找到最顶上了,即parent是null
// 2)找到某个节点是父节点的左孩子了
return parent;
}
}
/**
* 得到某个节点最左的孩子
*/
private static Node getMaxLeft(Node right) {
if (right == null) {
return null;
}
while (right.left != null) {
right = right.left;
}
return right;
}
二、纸条折痕问题
这是微软曾经的一道面试题,这题真的很考察一个人的能力,并不是说它很难,而是考察对算法的一种融会贯通的能力。
1、题目描述
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。此时折痕是凹下去的(下折痕),即折痕突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折2次,压出折痕后展开,此时有三条折痕,从上到下依次是下折痕、下折痕和上折痕。
给定一个输入参数N,代表纸条从下边向上方连续对折N次。请从上到下打印所有折痕的方向。
例如:
N=1时,打印: down(凹);
N=2时,打印: down(凹)、down(凹)、up(凸)
2、思路
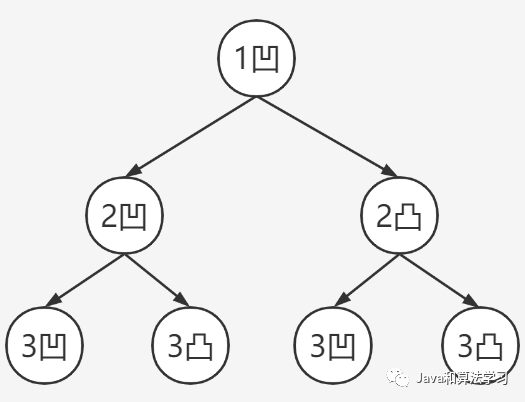
通过多次对折会发现:下一次的折痕对于上一次而言,总是上凹下凸的。
也就是第二次的折痕,在第一次的凹(1凹)上面是凹(2凹)、下面是凸(2凸);
第三次的折痕,在2凹的上面是3凹、下面是3凸,在2凸的上面是3凹、下面是3凸;以此类推。
然后依次展开,放到一个二叉树上,惊奇的发现,从上到下打印所有折痕的方向,就是二叉树的中序遍历。
3、代码
/**
* @author Java和算法学习:周一
*/
public static void paperFolding(int n) {
// 二叉树头节点是凹的
process(1, n, true);
}
/**
* @param i 节点的层数
* @param n 一共多少层
* @param down true=凹,false=凸
*/
private static void process(int i, int n, boolean down) {
if (i > n) {
return;
}
// 上边是凹
process(i + 1, n, true);
System.out.print(down ? "凹 " : "凸 ");
// 下边是凸
process(i + 1, n, false);
}
是不是发现,思路对了一下就豁然开朗了,融会贯通也是一种能力。