文章目录
数组
数组的存储结构
在设计数组的存储结构时,通常将数组的所有元素存储到存储器的一块地址连续的内存单元中,即数组特别适合采用顺序存储结构来存储。
一维数组的存储结构
对于一维数组(a
1
,a
2
,···,a
i
,···,a
n
),按元素顺序存储到一块地址连续的内存单元中,假设第一个元素a
1
的存储地址用LOC(a
1
)表示,每个元素占用k个存储单元,则任一数组元素ai的存储地址LOC(a
i
)可用以下公式求出:
LOC(a
i
) = LOC(a
1
) + ( i – 1 ) * k (i>=2&&i<=n)
二维数组的存储结构
对于一个m行n列的二维数组A[m][n]:

一、二维数组按行优先存放
即先存储第1行,紧接着存储第2行······依此类推,最后存储第m行

最终的存储示意图:

按照行优存放时,任一一个元素a[i][j]的存储地址可以得出:
(假设第一个元素a[1][1]的存储地址为LOC(a[1][1])表示,每个元素占用k个存储单元)

LOC(a[i][j]) = LOC(a[1][1]) + [( i – 1) * n + ( j – 1 )] * k
二、二维数组按列优先存放
即先存储第1列,紧接着存储第2列······依此类推,最后存储第m列
同理如“按行优先存放的推导过程”
按照列优存放时,任一一个元素a[i][j]的存储地址可以得出:
(假设第一个元素a[1][1]的存储地址为LOC(a[1][1])表示,每个元素占用k个存储单元)
LOC(a[i][j]) = LOC(a[1][1]) + [( j – 1 ) * m + ( i – 1 )] * k
特殊矩阵的压缩存储
一、对称矩阵的压缩存储
若一个n阶方阵A[n][n]中的元素满足a[i][j]=a[j][i](0≤i,j≤n-1),则称其为n阶
对称矩阵
。

以行序为主序存储其下三角+主对角线的元素。

下三角+主对角线的元素存储的下标k与二维数组中的下标i,j的对应关系:

上三角的元素存储(上三角元素值与下三角值对称相等):

整个对称矩阵的压缩存储:

二、上、下三角矩阵的压缩存储
上三角矩阵
上三角矩阵的特点是:下三角为一个固定的常数c。
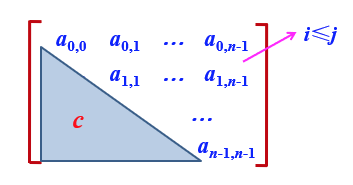
上三角的压缩存储示意图:

上三角+主对角线的元素存储的下标k与二维数组中的下标i,j的对应关系:

下三角矩阵
下三角矩阵的特点是:上三角为一个固定的常数c。
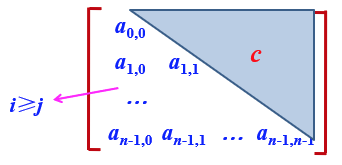
上三角的压缩存储示意图:

上三角+主对角线的元素存储的下标k与二维数组中的下标i,j的对应关系:

三、对角矩阵的压缩存储

对称矩阵的压缩存储示意图以及对应关系:

- 学习数据结构教程(第五版)——李春葆教授主编
- 图片来源于MOOC,数据结构——武汉大学——李春葆教授
- (如若侵权可联系QQ删除)