1.跳跃游戏简单介绍
跳跃游戏是一种典型的算法题目,经常是给定一数组arr[],从数组的某一位置i出发,根据一定的跳跃规则,比如从i位置能跳arr[i]步,或者小于arr[i]步,或者固定步数,直到到达某一位置,可能是数组的最后一个位置,也有可能是某一特别的数值处。

对于跳跃游戏类的题目,经常使用贪心、动态规划、dfs、bfs等方法解决,对于可以使用贪心解决的题目,经常也可以使用动态规划,但一般贪心可以有更好的时间复杂度和空间复杂度。
2.跳跃游戏相关专题
1.leetcode55 跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。本题属于跳跃游戏的基础题,要判断是否能跳到最后一格,按照最极端的情况来说,只要数组中没有0这一元素,是肯定可以跳到最后一格的(题目规定0 <= nums[i] <= 105)。
假如碰到了一个0,只要从这一元素向前找,找到可以跳过这个障碍的大的元素即可。

class Solution {
public boolean canJump(int[] nums) {
int end = nums.length-1;
for(int i = 0; i < end; i++){
if(nums[i] == 0){
int left = i-1;
while(left >= 0){
if(nums[left] + left > i){
break;
}
left--;
}
if(left == -1) return false;
continue;
}
}
return true;
}
}
但是本方法会在碰到0的时候不断向前搜索,耗费时间,属于暴力搜索,也可以考虑从后向前搜索,这种方法不需要回退,碰到0向前搜索可以越过此障碍的元素,在找到之后就不需要进行回退,一次成型。

class Solution {
public boolean canJump(int[] nums) {
int index = nums.length-1;
int len = nums.length;
if(index+1 <= 1) return true;
boolean flag = true;
while(index >= 0){
if(nums[index] != 0){
index--;
continue;
}
for(int left = index-1; left >= 0; left--){
if(nums[left] > index-left || nums[left]+left >= len-1){
index = left;
flag = false;
break;
}
}
if(!flag){
flag = true;
continue;
}
return false;
}
return true;
}
}代码未优化,但本质是O(N),比第一种方法要快一些。另外,基于贪心的思想【1】:
如果某一个作为 起跳点 的格子可以跳跃的距离是 3,那么表示后面 3 个格子都可以作为 起跳点
可以对每一个能作为 起跳点 的格子都尝试跳一次,把 能跳到最远的距离 不断更新
如果可以一直跳到最后,就成功了
class Solution {
public boolean canJump(int[] nums) {
int cover = nums[0];
for(int i = 0; i < nums.length; i++){
if(i > cover) return false;
cover = Math.max(cover,i+nums[i]);
}
return true;
}
}

基于相同思想的贪心算法【2】:
贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。
class Solution {
public boolean canJump(int[] nums) {
int cover = nums[0];
for(int i = 0; i <= cover; i++){
cover = Math.max(cover,i+nums[i]);
if(i+nums[i] >= nums.length-1) return true;
}
return false;
}
}
2.leetcode45 跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]
i + j < n
返回到达 nums[n – 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n – 1]。
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
动态规划【3】:
class Solution {
public int jump(int[] nums) {
int[] dp = new int[nums.length];
dp[0] = 0;
for (int i = 1; i < dp.length; i++) {
dp[i] = nums.length + 1;
}
for (int i = 1; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (j + nums[j] >= i) {
dp[i] = Math.min(dp[i], dp[j] + 1);
}
}
}
return dp[dp.length - 1];
}
}

优化动态规划【3】:
在上述方法中,走了很多不需要的步骤,可以进行优化
class Solution {
public int jump(int[] nums) {
int[] dp = new int[nums.length];
dp[0] = 0;
for (int i = 1; i < dp.length; i++) {
dp[i] = nums.length + 1;
}
for (int i = 0; i < nums.length; i++) {
for (int j = 1; j <= nums[i]; j++ ) {
if (i + j >= nums.length) {
return dp[dp.length - 1];
}
dp[i + j] = Math.min(dp[i + j], dp[i] + 1);
}
}
return dp[dp.length - 1];
}
}

贪心【4】:
class Solution {
public int jump(int[] nums) {
// 记录当前能跳跃到的位置的边界下标
int border = 0;
// 记录在边界范围内,能跳跃的最远位置的下标
int maxPosition = 0;
// 记录所用步数
int steps = 0;
for(int i=0;i<nums.length-1;i++){
// 继续往下遍历,统计边界范围内,哪一格能跳得更远,每走一步就更新一次能跳跃的最远位置下标
// 其实就是在统计下一步的最优情况
maxPosition = Math.max(maxPosition,nums[i]+i);
// 如果到达了边界,那么一定要跳了,下一跳的边界下标就是之前统计的最优情况maxPosition,并且步数加1
if(i==border){
border = maxPosition;
steps++;
}
}
return steps;
}
}
3.leetcode1306 跳跃游戏 III
这里有一个非负整数数组 arr,你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时,你可以跳到 i + arr[i] 或者 i – arr[i]。
请你判断自己是否能够跳到对应元素值为 0 的 任一 下标处。
注意,不管是什么情况下,你都无法跳到数组之外。
输入:arr = [4,2,3,0,3,1,2], start = 5
输出:true
解释:
到达值为 0 的下标 3 有以下可能方案:
下标 5 -> 下标 4 -> 下标 1 -> 下标 3
下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3
class Solution {
public boolean canReach(int[] arr, int start) {
boolean[] visited = new boolean[arr.length];
return dfs(arr,start,visited);
}
public boolean dfs(int[] arr, int index, boolean[] visited){
if(index < 0 || index >= arr.length || visited[index]) return false;
if(arr[index] == 0) return true;
visited[index] = true;
return dfs(arr,index+arr[index],visited) || dfs(arr,index-arr[index],visited);
}
}
本题小结:(1)典型的dfs题目
(2)注意用 visited保存走过的路径即可
助于理解,更多的【6】:
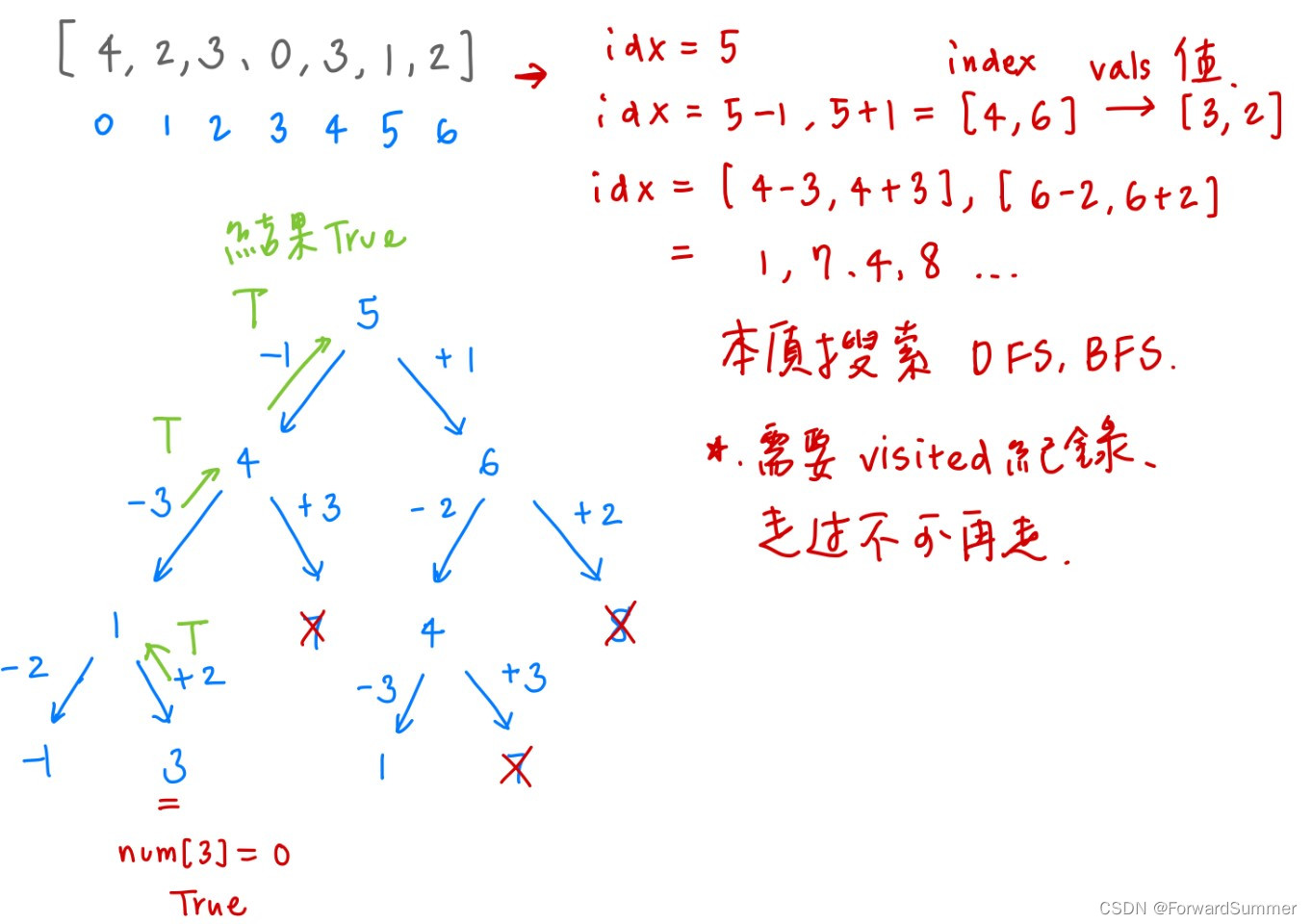
参考来源
【1】leetcode Ikaruga
【跳跃游戏】别想那么多,就挨着跳吧
【2】leetcode 代码随想录 「
代码随想录」带你学透贪心算法!55. 跳跃游戏
【3】leetcode alchemist
动态规划 跳跃游戏 II
【4】leetcode 風居住的街道
【跳跃游戏 II】别想那么多,就挨着跳吧 II
【5】leetcode Ikaruga
【跳跃游戏 II】别想那么多,就挨着跳吧 II
【6】leetcode fake_panda
Java BFS + DFS 浅显易懂 附上递归树图