定义
给出两个字符串 str1 和 str2,返回同时以 str1 和 str2 作为子序列的最短字符串。如果答案不止一个,则可以返回满足条件的任意一个答案。
(如果从字符串 T 中删除一些字符(也可能不删除,并且选出的这些字符可以位于 T 中的 任意位置),可以得到字符串 S,那么 S 就是 T 的子序列)
样例1
输入:str1 = “abac”, str2 = “cab”
输出:“cabac”
解释:删去 “
c
abac” 第一个字母的 “c” 得到 “abac”。
删去 “cab
ac
” 最后两个字母 “ac” 得到 “cab”。
样例2
输入:str1 = “AABXFGA”, str2 = “ABAAXGF”
输出:“ABAABXGFGA”
解释:删去 “
AB
AABX
G
FGA” 加黑字母 得到”AABXFGA”。
删去 “ABAA
B
XGF
GA
“加黑字母”ABAAXGF”。
递推公式
最短公共超序列和
最长公共子序列
有些相似、
设序列X={x1,x2…xm},Y={y1,y2…yn}
X与Y的最短公共超序列为Z={z1,z2…zk}(z都是x和y序列中的字符)
dp(m,n)表示序列X的前m项和序列Y的前n项的最短公共超序列的位数
-
当X(Y)至少有一个序列为空时:
此时最短公共超序列z一定要包含X(Y)全部字符,而求最短公共超序列,于是最短公共超序列就是X(Y)
Y为空时:dp(i,0)=i (1<=i<=m)
X为空时:dp(0,j)=j (1<=j<=n)
-
当Xm=Yn时
此时,该字母一定包含在最短公共超序列中,相等就只需要加一个就好啦。(比如x中是a,y中也是a,最短公共超序列中只需要加一个a就行了)
dp(m,n)=dp(m-1,n-1)+1
- 当Xm!=Yn时, 当xm(yn)为最短公共超序列中需要新添加的一个字符时(x出现了一个从来没出来的字符)
dp[i][j]=dp[i-1][j]+1
dp[i][j]=dp[i][j-1]+1
则递推公式为:

样例过程图解
str1 = “AABXFGA”,
str2 = “ABAAXGF”
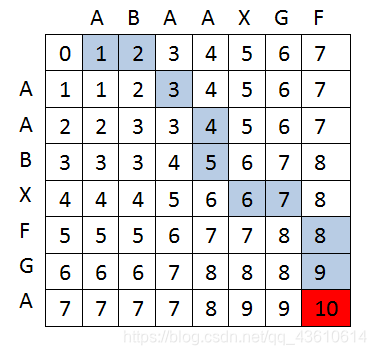
10为最后的结果,蓝色代表其中的一种解
c语言代码
#include <stdio.h>
#include <string.h>
int max(int a,int b)
{
if(a>b)
return a;
else return b;
}
int min(int a,int b)
{
if(a<b)
return a;
else return b;
}
int dp[105][105],len1,len2,cou=0;
char a[105],b[105],c[105]; //a,b用来存放输入的两个字符串,c存放最短公共超序列的一种解
int main()
{ int i,j;
scanf("%s",&a);
scanf("%s",&b);
len1=strlen(a);
len2=strlen(b);
for(i=strlen(a);i>0;i--) //为了方便dp数组的操作,我将字符往后移动一位
a[i]=a[i-1];
for(i=strlen(b);i>0;i--)
b[i]=b[i-1];
a[0]='0'; //随便给的值
b[0]='1';
for(i=0;i<=max(len1,len2);i++) //当某个字符串为空时,赋初值
dp[i][0]=dp[0][i]=i;
for(i=1;i<=len1;i++)
{
for(j=1;j<=len2;j++)
{
if(a[i]==b[j])
dp[i][j]=dp[i-1][j-1]+1; //根据递推公式求dp()
else
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+1;
}
}
i=len1;
j=len2;
while(i>0&&j>0) //根据比较最后的值是怎么来的,计算出最短超序列的一种解
{
if(dp[i][j]==dp[i-1][j-1]+1&&a[i]==b[j]) //相等时
{
c[cou]=a[i];
cou++;
i--;
j--;
}
else if(dp[i][j]==dp[i-1][j]+1&&a[i]!=b[j])//来自a
{
c[cou]=a[i];
cou++;
i--;
}
else if(dp[i][j]==dp[i][j-1]+1&&a[i]!=b[j])//来自b
{
c[cou]=b[j];
cou++;
j--;
}
}
while(i>0) //输入的字符串大小不等,或者在a,b中选取的个数不相等时,若第0行或者第0列没有选完时
{
c[cou]=a[i];
i--;
cou++;
}
while(j>0)
{
c[cou]=b[j];
j--;
cou++;
}
for(i=strlen(c)-1;i>=0;i--) //输出其中一个最短超序列
printf("%c",c[i]);
printf("\n");
printf("\n%d",dp[len1][len2]);
return 0;
}