博客

线性回归和逻辑回归：回归指的是求连续函数上的预测值

线性回归LossFunction：


均方误差损失函数(

MSE)

梯度反向传播更新参数：

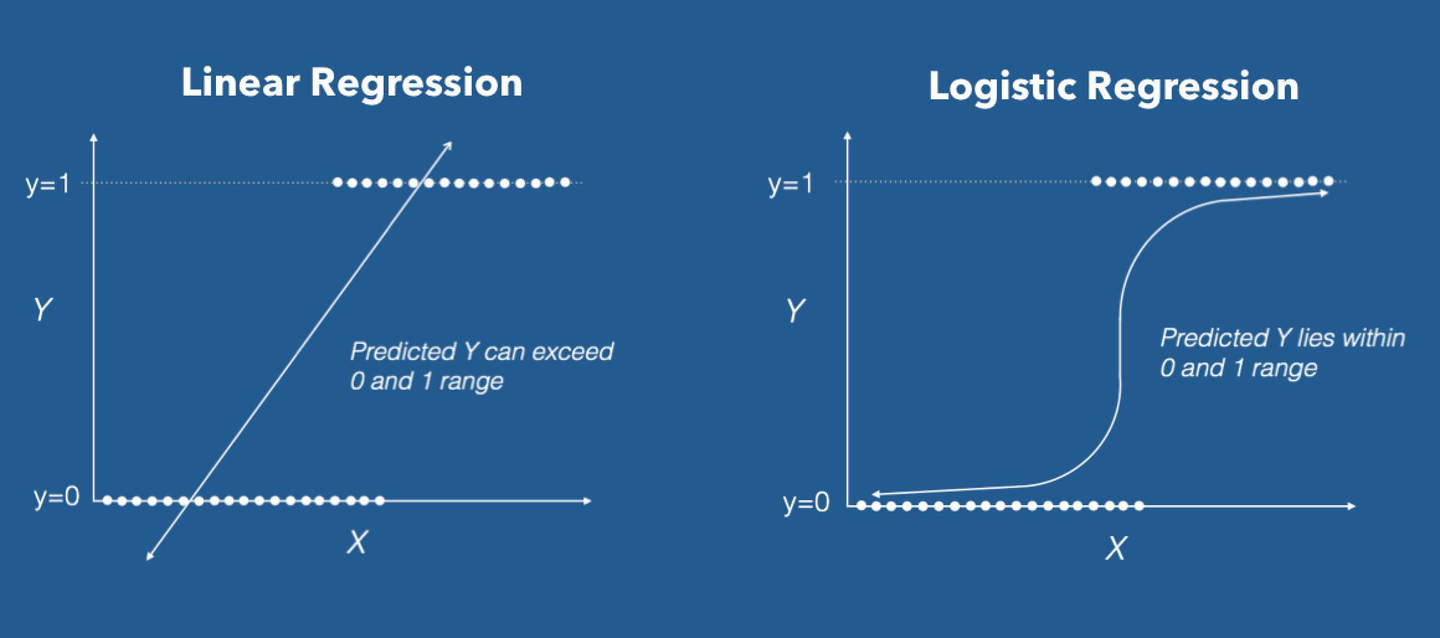
逻辑回归：线性回归的推广

线性回归应用到

分类问题

中，比如二分类问题，将X对应的y分为类别0和类别1。即逻辑回归是将线性回归本身的输出是连续的值分为离散的0和1，其中将利用一个联系函数，将X映射到y∈{0，1}

逻辑回归使用的联系函数是Sigmoid函数（S形函数）中的最佳代表，即对数几率函数（Logistic Function）

损失函数为交叉熵损失函数：因为使用了sigmoid函数，所以sigmoid梯度如下所示

增加特征的方法，

def mapFeature(x1, x2):
    """ 创作多些feature防止偏差大
    degree=2, project into 1,x1,x2,x1^2,x1x2,x2^2"""
    degree = 2
    out = np.ones((x1.shape[0], 1))  # 映射后的结果数组（取代X）
    for i in np.arange(1, degree+1):
        for j in range(i+1):
            tmp = x1**(i-j)*(x2**j)
            out = np.hstack((out, tmp.reshape(-1,1)))
    return out

对损失函数求偏导之后发现和线性回归是一样的结果：

正则化：为了防止过拟合在后面加上L2正则化

其中j从1开始，因为X最前面一列加上一列1所以，theta[0]是常数项，没必要正则化。

所以损失函数的梯度求导需要算上正则化的梯度：

三：神经网络

12.2 梯度检查 – AI-EDU

神经网络算法使用反向传播计算目标函数关于每个参数的梯度，可以看做解析梯度。由于计算过程中涉及到的参数很多，用代码实现的反向传播计算的梯度很容易出现误差，导致最后迭代得到效果很差的参数值。

为了确认代码中反向传播计算的梯度是否正确，可以采用梯度检验（gradient check）的方法。通过计算数值梯度，得到梯度的近似值，然后和反向传播得到的梯度进行比较，若两者相差很小的话则证明反向传播的代码是正确无误的。