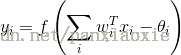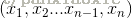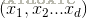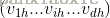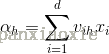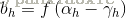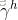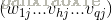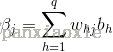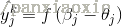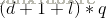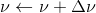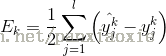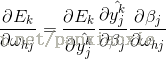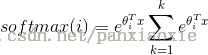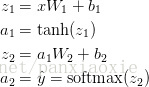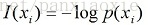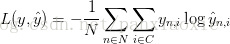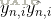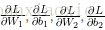神经网络python实现

写这篇博文主要是在帮助自己理解和记忆，以及方便自己以后查询，内容非原创。（我还没这水平，希望以后有 – – ）

参考内容：

[从头开始实现神经网络：入门]

(

http://python.jobbole.com/82208/

)

原英文版

Implementing a Neural Network from Scratch – An Introduction

周志华教授：《机器学习》

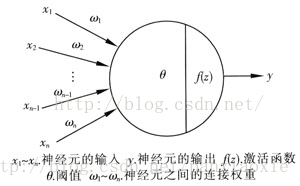
一、神经元模型

这里写图片描述

其中，

表示输入为一个样本的

n

维特征，神经元接受来自

n

个其他神经元的输入信号，通过权重后进行传递，神经元的总输入值与阈值进行比较，然后通过激活函数处理，产生神经元的输出。

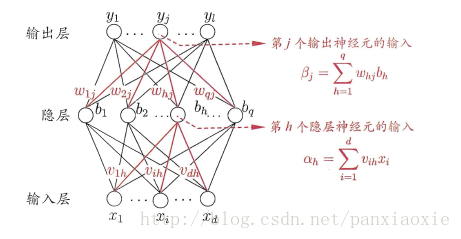
二、BP神经网络

在周志华博士的书中讲解的是BP神经网络，隐藏层和输出层的激活函数都是sigmoid函数。

其中：

输入层神经元：
这里写图片描述
表示输入的样本由

d

个属性描述。

输入层到隐藏层：

需要学习得到的

d*q

个权重参数

隐藏层神经元：

输入：

输出：
这里写图片描述
其中需要学习得到

q

个神经元阈值

隐藏层到输出层：

需要学习得到的

l*q

个权重参数

输出层神经元：

输入：
这里写图片描述

输出：

总共需要学习的参数个数：

，

更新估计式为：

神经网络的cost函数：

BP算法以梯度下降（gradient descent）策略，以目标的负梯度方向对参数进行调整。

以参数whj为例：

这里写图片描述

可以观察Whj是怎么影响到Ek的，首先先影响/beta j,然后影响输出值hat{y_{j}^{k}} ,因此有：

$\frac{\partial E_{k} }{\partial \omega_{hj}} = \frac{\partial E_{k}}{\partial \hat{y_{j}^{k}}}·\frac{\partial \hat{y_{j}^{k}} }{\partial \beta_{j}}·\frac{\partial \beta_{j}}{\partial \omega_{hj}}$

公式太多，就直接手写推导过程了

这里写图片描述

神经网络的python实现

接下来的内容会从头实现一个简单的3层神经网络。

一、产生数据集

让我们从力所能及的产生数据集开始吧。幸运的是，scikit-learn提供了一些很有用的数据集产生器，所以我们不需要自己写代码了。我们将从make_moons 函数开始。

###generate a dataset and plot it
from sklearn import datasets
import matplotlib.pyplot as plt

numpy.random.seed(0) 
##seed() 方法改变随机数生成器的种子，可以在调用其他随机模块函数之前调用此函数。。
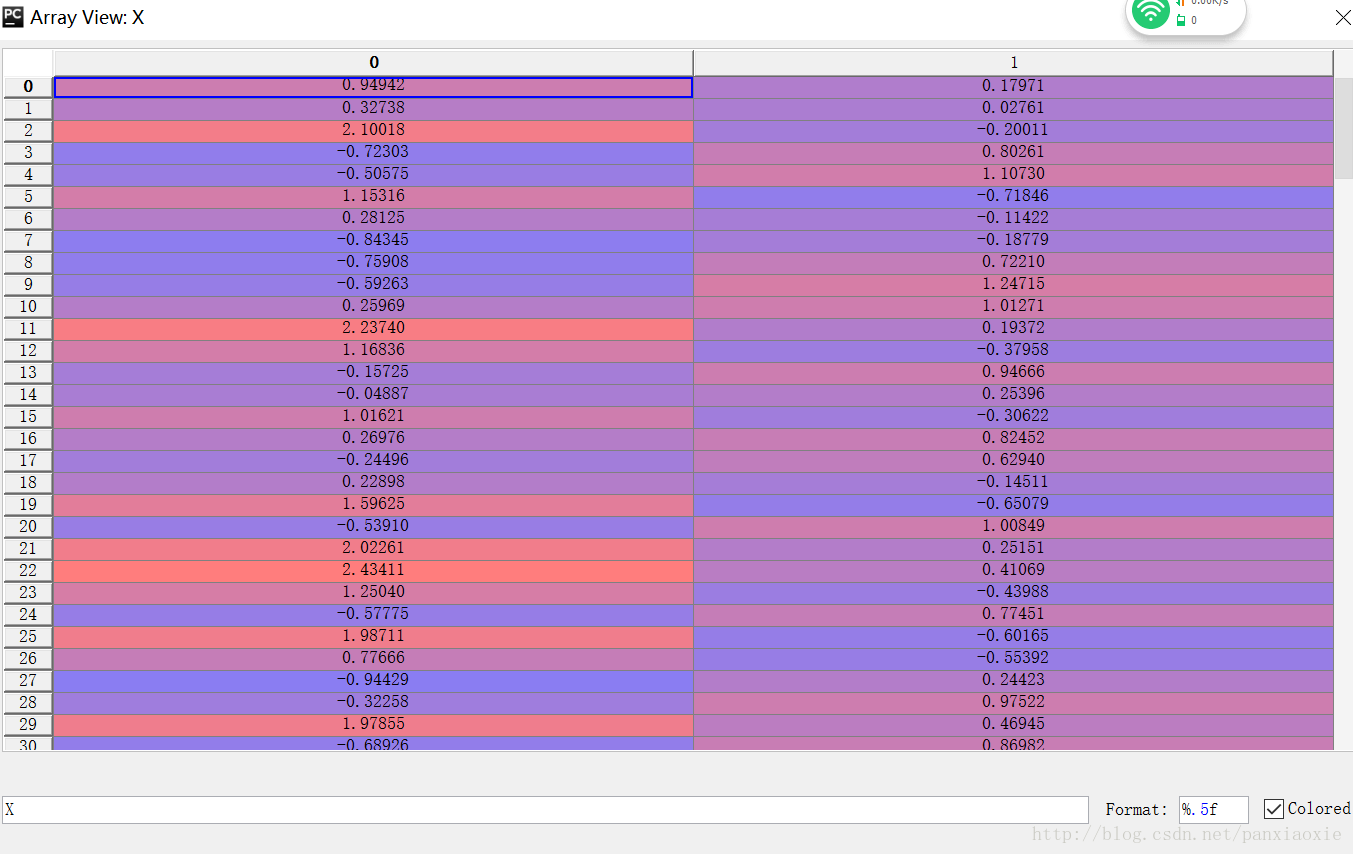
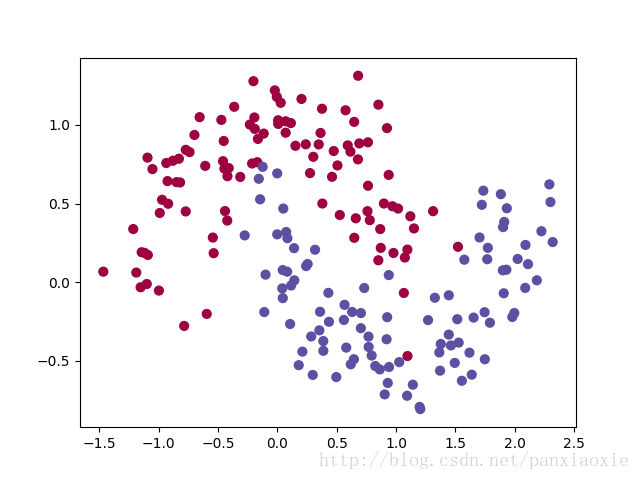
X,y = datasets.make_moons(200,noise = 0.20)    
plt.scatter(X[:,0],X[:,1],s=40,c =y,cmap =plt.cm.Spectral )  
# plt.show()
#scatter()散点图
X:<class 'numpy.ndarray'> ##shape(200,2)##[[0.496,0.2633],[0.496,0.2633]...]  随意举例
y:<class 'numpy.ndarray'> ##shape(200,)[0,1,1,0,1,1,0,1,1,1,0,0,0,1,1,1,0.....]

关于数据集

Sklearn 快速入门

这里生成两个交叉半圆的数据集。

这里写图片描述

当noise = 0时，数据集是这样的

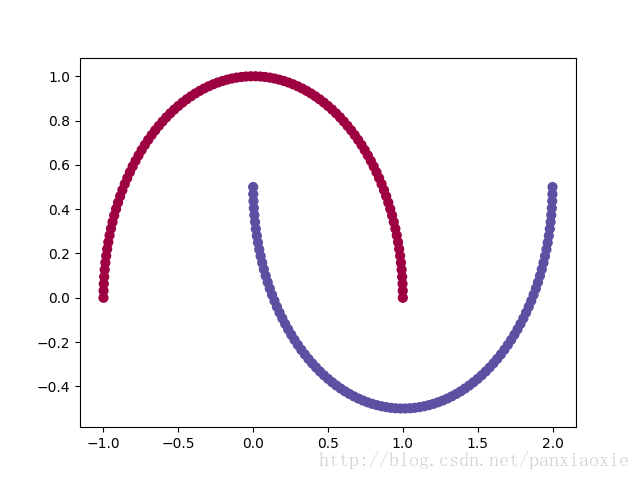
noise=0

二、Logistic回归

from sklearn import linear_model
clf = linear_model.LogisticRegressionCV()
clf.fit(X,y)

##注释
##The mod:`sklearn.linear_model`module implements generalized linear models. It includes Ridge regression, Bayesian Regression, Lasso and Elastic Net estimators computed with Least Angle Regression and coordinate descent. It also implements Stochastic Gradient Descent related algorithms.采用随机梯度下降
##LogisticRegressionCV  源代码表示好复杂，猜想应该就是采用随机梯度下降求解权重吧？？
##def fit(self, X, y, sample_weight=None):
    #Fit the model according to the given training data.策边界

# 咱们先画一个一个函数来画决策边界
def plot_decision_boundary(pred_func):
    # 设定最大最小值，附加一点点边缘填充
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01

    xx, yy = numpy.meshgrid(numpy.arange(x_min, x_max, h), numpy.arange(y_min, y_max, h))

    # 用预测函数预测一下
    Z = pred_func(numpy.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # 然后画出图
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)

plot_decision_boundary(lambda x:clf.predict(x))
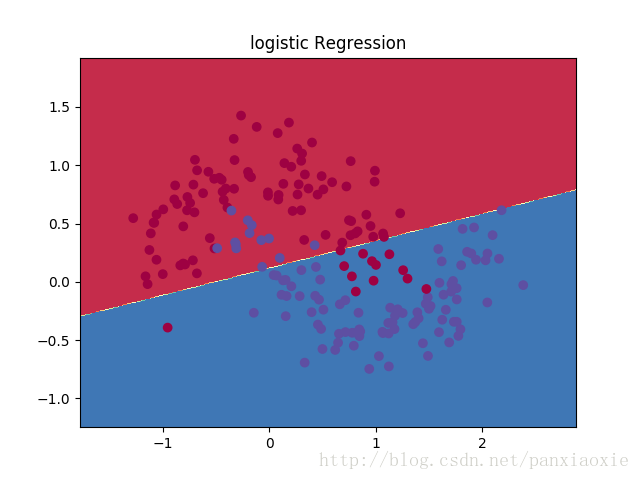
plt.title("logistic Regression")
# plt.show()

#注释
#arange(start=None, stop=None, step=None, dtype=None) 定义坐标间距和起始点 Return evenly spaced values within a given interval.
#meshgrid(*xi, **kwargs)  定义坐标    Return coordinate matrices from coordinate vectors.
#reshaper()      Give a new shape to the array without changing its data. 
#xx:<class 'tuple'>: (317, 486)
#clf.predict()   这里还是不能太理解，怎么就画出决策边界了？？ Predict class labels for samples in X.

这里写图片描述

上图展示了Logistic回归分类器学习到的决策边界。使用一条直线尽量将数据分离开来，但它并不能捕捉到数据的“月形”特征。

三、训练网络

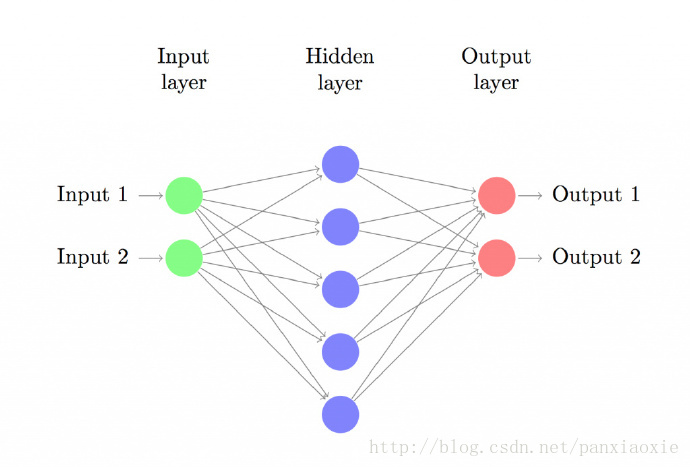
让我们来建立具有一个输入层、一个隐藏层、一个输出层的三层神经网络。输入层的结点数由数据维度决定，这里是2维。类似地，输出层的结点数由类别数决定，也是2。（因为我们只有两类输出，实际中我们会避免只使用一个输出结点预测0和1，而是使用两个输出结点以使网络以后能很容易地扩展到更多类别）。网络的输入是x和y坐标，输出是概率，一个是0（女性）的概率，一个是1（男性）的概率。它看起来像下面这样：

这里写图片描述

我们可以为隐藏层选择维度（结点数）。放入隐藏层的结点越多，我们能训练的函数就越复杂。但是维度过高也是有代价的。首先，预测和学习网络的参数就需要更多的计算。参数越多就意味着我们可能会过度拟合数据。

3.1 激活函数的选择

隐藏层激活函数：激活函数将该层的输入转换为输出。一个非线性激活函数允许我们拟合非线性假设。常用的激活函数有tanh、the sigmoid函数或者是ReLUs。这里我们选择使用在很多场景下都能表现很好的tanh函数。这些函数的一个优点是它们的导数可以使用原函数值计算出来。例如，tanh x的导数是1-tanh^2 x。这个特性是很有用的，它使得我们只需要计算一次tanh x值，之后只需要重复使用这个值就可以得到导数值。

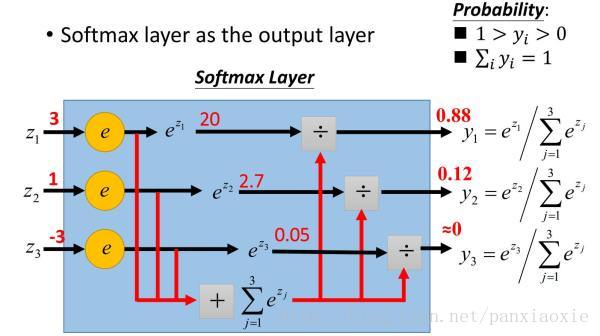
输出层激活函数：因为我们想要得到神经网络输出概率，所以输出层的激活函数就要是softmax。这是一种将原始分数转换为概率的方法。如果你很熟悉logistic回归，可以把softmax看作是它在多类别上的一般化。

softmax函数：

表达式：
这里写图片描述

softmax把一个k维的real value向量（a1,a2,a3,a4….）映射成一个（b1,b2,b3,b4….）其中bi是一个0-1的常数，然后可以根据bi的大小来进行多分类的任务，如取权重最大的一维。

3.2 前向传播

ai表示输入层，zi表示输出层。第一层网络的输入是a1，输出是z1，第二层网络的输入a2，输出是z2

这里写图片描述

W1,b1,W2,b2是需要从训练数据中学习的网络参数。你可以把它们看作是神经网络各层之间数据转换矩阵。

3.3 损失函数

损失函数：学习该网络的参数意味着要找到使训练集上错误率最小化的参数(W1,b1,W2,b2)。但是如何定义错误率呢？我们把衡量错误率的函数叫做损失函数（loss function）。输出层为softmax时多会选择

交叉熵损失

（cross-entropy loss）。

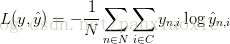
这里写图片描述

信息论的熵

熵的定义：随机事件自信息量的期望，不确定度的期望。

自信息量：一个事件（消息）本身所包含的信息量，由事件的不确定性决定的。

则熵表示为：

那么什么是交叉熵？

交叉熵和相对熵


交叉熵

这里面

分别表示真实标签值，和预测标签值。

预测标签值能理解，就是输出层的softmax得到的输出，是个概率分布。但真实标签值不就是1或0吗？？？？

当预测值和标签值越差距越小时，交叉熵越小。那么我们的目标是找到能最小化损失函数的参数值。我们可以使用梯度下降方法找到最小值。我会实现梯度下降的一种最普通的版本，也叫做有固定学习速率的批量梯度下降法。诸如SGD（随机梯度下降）或minibatch梯度下降通常在实践中有更好的表现。所以，如果你是认真的，这些可能才是你的选择，最好还能逐步衰减学习率。

3.4 学习参数

作为输入，梯度下降需要一个与参数相关的损失函数的梯度（导数矢量）：
这里写图片描述
。

为了计算这些梯度，我们使用了著名的后向传播算法。这个算法是从输出计算梯度的一种很高效的方法。与BP神经网络类似，运用链式法则进行求导。

求导过程：

求导结果：

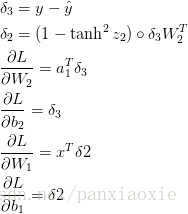
这里写图片描述

3.5代码实现

3.5.1 从定义梯度下降一些有用的变量和参数开始：

###定义一些参数和标量
num_example = len(X) # training set size
nn_inumpyut_dim = 2 #inumpyut layer dimensionality
nn_output_dim = 2 #output layer dimensionality

epsilon = 0.01  #learning rte for gradient decent
reg_lambda = 0.01 #regularization strength 正则化强度

关于正则化的理解：

机器学习之正则化

3.5.2损失函数

首先要实现我们上面定义的损失函数。以此来衡量我们的模型工作得如何：

###定义损失函数
def calculate_loss(model):
    W1,b1,W2,b2 = model['W1'],model['b1'],model['W2'],model['b2']
    # Forward propagation to calculate our predictions
    z1 = X.dot(W1) + b1 ##这里不太理解dot，矩阵相乘？
    a1 = numpy.tanh(z1)
    z2 =a1.dot(W2) + b2
    exp_score = numpy.exp(z2)
    # output 输出值 hat{y}
    probs = exp_score/numpy.sum(exp_score , axis=1 ,keepdims= True)  ##(200,2)
    # Calculating the loss  损失函数
    corect_logprobs = -numpy.log(probs[range(num_example),y])
    ##(200，) 这里是对每个样本C个分类，即2个特征的累加
    data_loss = numpy.sum(corect_logprobs)
    ##这里是对所有样本的一个累加，所以是一个实数
    # Add regulatization term to loss (optional)  正则化项
    data_loss += reg_lambda/2*(numpy.sum(numpy.square(W1))+numpy.sum(numpy.square(W1)))
    return 1./num_example*data_loss

3.5.3 计算网络的输出

它的工作就是传递前面定义的前向传播并返回概率最高的类别。

# Helper function to predict an output (0 or 1)
def predict(model, x):
    W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
    # Forward propagation
    z1 = x.dot(W1) + b1
    a1 = numpy.tanh(z1)
    z2 = a1.dot(W2) + b2
    exp_scores = numpy.exp(z2)
    probs = exp_scores / numpy.sum(exp_scores, axis=1, keepdims=True)
    return numpy.argmax(probs, axis=1)

这里argmax是取最大值的索引，是进行轴上的比较。

axis = 0: 你就这么想，0是最大的范围，所有的数组都要进行比较，只是比较的是这些数组相同位置上的数

axis = 1: 等于1的时候，比较范围缩小了，只会比较每个数组内的数的大小，结果也会根据有几个数组，产生几个结果

那么在这里axis=1,应该怎么理解呢？就是每个样本里面有两个输出（0和1），输出概率较大的就是我们的预测值！！！！！！！！！

*

好爽~~！！！*

3.5.4训练神经网络的函数

即使用上文中发现的后向传播导数实现

批量梯度下降

。其实，随机梯度下降更好，对吧！

# This function learns parameters for the neural network and returns the model.
# - nn_hdim: Number of nodes in the hidden layer
# - num_passes: Number of passes through the training data for gradient descent
# - print_loss: If True, print the loss every 1000 iterations
def build_model(nn_hdim, num_passes=20000, print_loss=False):
    # Initialize the parameters to random values. We need to learn these.
    numpy.random.seed(0)
    W1 = numpy.random.randn(nn_inumpyut_dim, nn_hdim) / numpy.sqrt(nn_inumpyut_dim)
    ##Return a sample (or samples) from the "standard normal" distribution. 其中shape = （输入层节点数，隐藏层节点数） 为什么要除以sqrt(2)
    b1 = numpy.zeros((1, nn_hdim))    ###阈值初始化为1
    W2 = numpy.random.randn(nn_hdim, nn_output_dim) / numpy.sqrt(nn_hdim)
    b2 = numpy.zeros((1, nn_output_dim))

    # This is what we return at the end
    model = {}   ##一个字典

    # Gradient descent. For each batch...批量梯度下降
    for i in xrange(0, num_passes):       ##xrange = range  这个迭代次数怎么选？？

        # Forward propagation
        z1 = X.dot(W1) + b1
        a1 = numpy.tanh(z1)
        z2 = a1.dot(W2) + b2
        exp_scores = numpy.exp(z2)
        probs = exp_scores / numpy.sum(exp_scores, axis=1, keepdims=True)

        # Backpropagation 反向传播，链式法则
        delta3 = probs   ## hat{y}  （200，2）
        delta3[range(num_example), y] -= 1  ##hat{y}-y  （200，2） 
        dW2 = (a1.T).dot(delta3)  # （3，2）输出层权重
        db2 = numpy.sum(delta3, axis=0, keepdims=True)  #（1，2）  delta3列向相加得到两个数
        delta2 = delta3.dot(W2.T) * (1 - numpy.power(a1, 2))  #（200，3） 输入层权重
        dW1 = numpy.dot(X.T, delta2)  ##（2，3）
        db1 = numpy.sum(delta2, axis=0)  ###（1，2）  delta2列向相加得到两个数

        # Add regularization terms (b1 and b2 don't have regularization terms)
        dW2 += reg_lambda * W2     ##正则项
        dW1 += reg_lambda * W1

        # Gradient descent parameter update
        W1 += -epsilon * dW1  ##梯度更新
        b1 += -epsilon * db1
        W2 += -epsilon * dW2
        b2 += -epsilon * db2

        # Assign new parameters to the model
        model = {'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}

        # Optionally print the loss.
        # This is expensive because it uses the whole dataset, so we don't want to do it too often.
        if print_loss and i % 1000 == 0:  #每1000次记录一下
            print("Loss after iteration %i: %f" % (i, calculate_loss(model)))

    return model
#
# Build a model with a 3-dimensional hidden layer
model = build_model(3, print_loss=True)

# Plot the decision boundary
plot_decision_boundary(lambda x: predict(model, x))
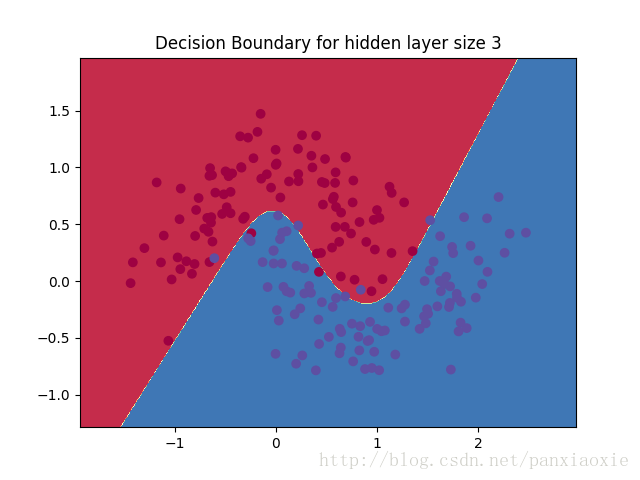
plt.title("Decision Boundary for hidden layer size 3")
plt.show()

运行结果：

Loss after iteration 0: 0.418184
Loss after iteration 1000: 0.075267
Loss after iteration 2000: 0.075641
Loss after iteration 3000: 0.075727
Loss after iteration 4000: 0.075753
Loss after iteration 5000: 0.075762
Loss after iteration 6000: 0.075765
Loss after iteration 7000: 0.075766
Loss after iteration 8000: 0.075766
Loss after iteration 9000: 0.075766
Loss after iteration 10000: 0.075766
Loss after iteration 11000: 0.075766
Loss after iteration 12000: 0.075766
Loss after iteration 13000: 0.075766
Loss after iteration 14000: 0.075766
Loss after iteration 15000: 0.075766
Loss after iteration 16000: 0.075766
Loss after iteration 17000: 0.075766
Loss after iteration 18000: 0.075766
Loss after iteration 19000: 0.075766
Loss after iteration 20000: 0.075766

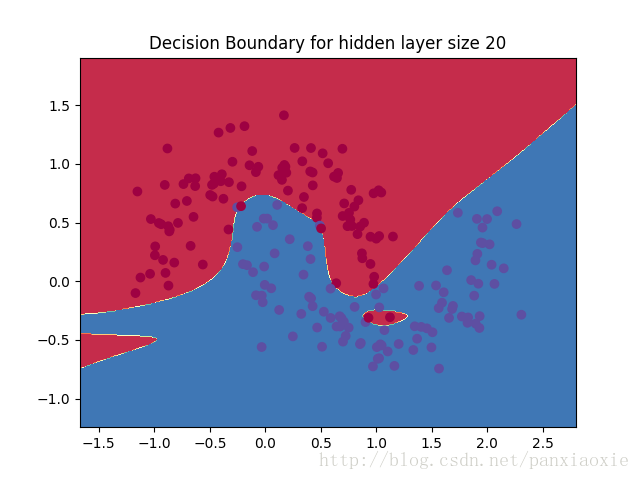
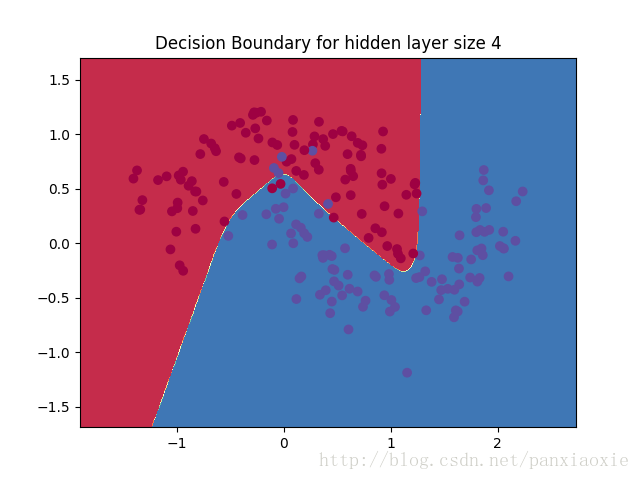
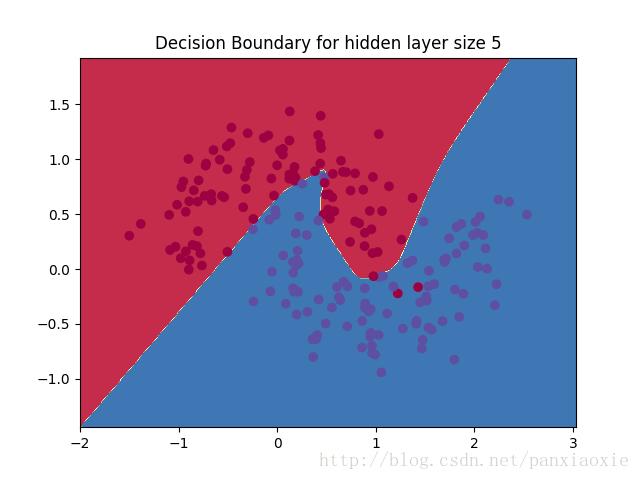
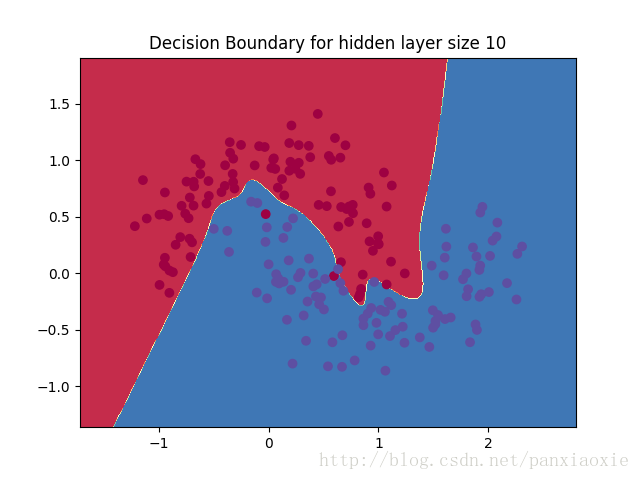
这里写图片描述

改变隐藏层的节点数后：

原文链接：https://blog.csdn.net/panxiaoxie/article/details/71939723

你可能也喜欢