1. 轧制单元
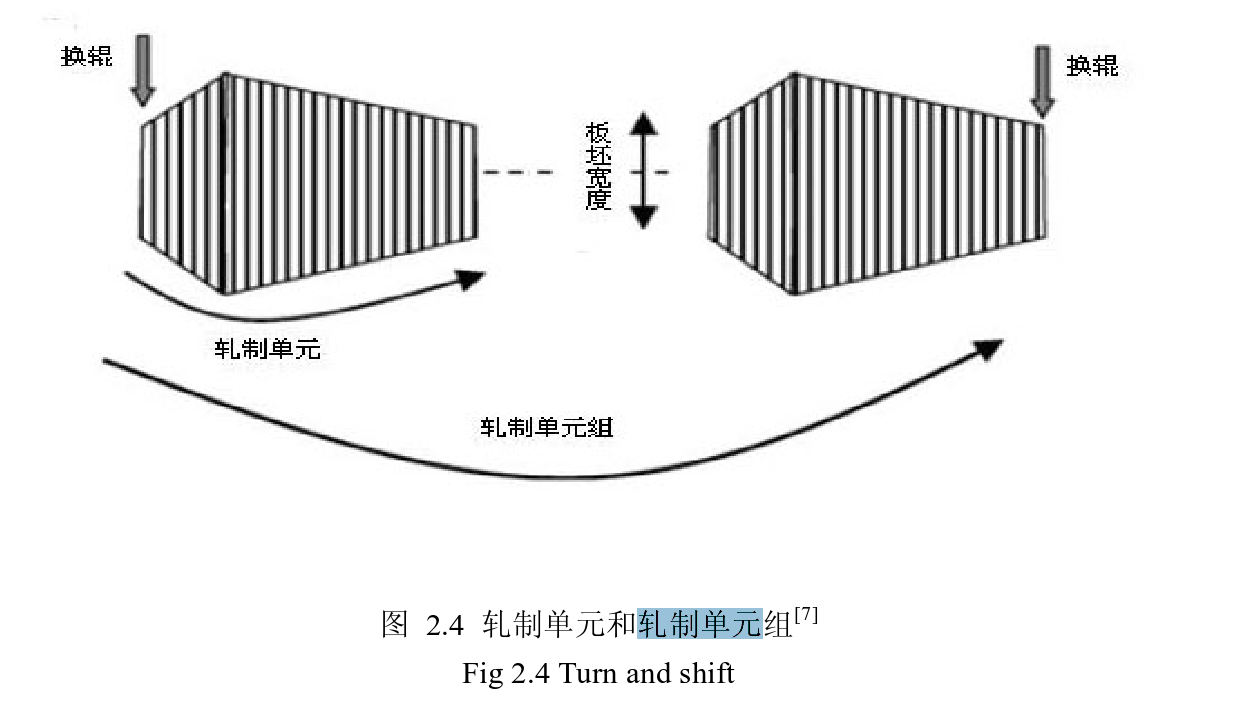
更换前后两个工作辊之间的轧制对象称为
轧制单元
,对应一个轧制计划。两个 支撑辊之间的轧制对象是由多个轧制单元组成,称为
轧制单元组
,对应多个轧制计 划。
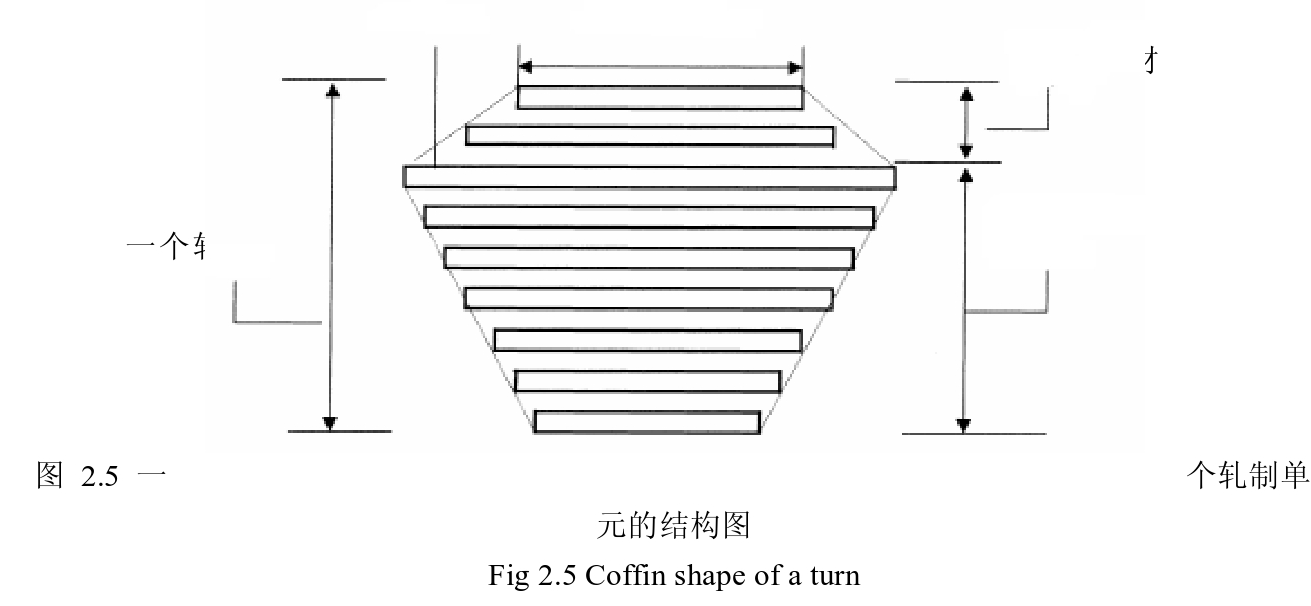
轧制单元的结构
每个计划开始的部分板坯按照宽度非减的方向排列来加热轧辊,这 部分板坯被称作“烫辊材”。相应的,轧制计划的主体部分被称作“主体材”。通常一个完整的轧制单元的轧件宽度具有“双梯形结构”,如上图所示。正梯 形是烫辊材部分,而反梯形是主体材部分。
主体材的宽度是由宽到窄变化的,最大正跳跃差为250mm,反跳跳跃差最大为20mm。主体材的总长度和总重量有一定限制,并且厚度、宽度和硬度不允许同时跳跃。
带钢厚度跳跃规程:

硬度组跳跃规程:
相邻两种硬度组的跳跃差最大为2。
2. 温度
出炉温度
:影响轧机负荷的合理分配。
终轧温度
:终轧温度对带钢质量有直接影响。终轧温度的高低,在很大程度上决定了轧后钢材内部的金相组织和力学性能。一般终轧温度在850℃左右,约为800-900℃。
卷曲温度
:卷曲温度应在680℃以下,约为550-650℃。在此温度阶段,带钢的金相组织已 定形,可以缓慢冷却,而且缓慢冷却对减小带钢的内应力也是有利的。过高的卷曲 温度,将会因卷曲后的再结晶和缓慢冷却而产生粗晶组织和碳化物的积聚。卷曲温 度过高还容易产生坚实的氧化铁皮,使酸洗困难。
在热轧过程,要求出炉温度、终轧温度和卷曲温度均匀变化,同时不能跳跃太大。一般情况下,出炉温度的最大跳跃值为30℃、终轧温度的最大跳跃值为60℃、 卷曲温度的最大跳跃值为90℃。
3. 旅行商问题
旅行商问题(Traveling Salesman Problem, TSP) 这个问题字面上的理解是:有一个推销员,要到n个城市推销商品,他要找出 一个包含所有n个城市的具有最短路程的环路。 TSP的历史很久,最早的描述是 1759年欧拉研究的骑士周游问题,即对于国际象棋棋盘中的64个方格,走访64个 方格一次且仅一次,并且最终返回到起始点。
TSP由美国RAND公司于1948年引入,该公司的声誉以及线性规划这一新方法的出现使得TSP成为一个知名且流行的 问题。由于限制条件的增加,TSP问题可以衍生出
多个旅行商问题(MTSP)
,就是 一个出发点,m个旅行商的TSP,即所访问的客户没有需求,车辆没有装载的限制, 优化目标就是要遍历所有的客户,达到总里程最短。
4.TSP的主要求解方法
(1)构造型算法(最先开发的求解算法,如最近邻点、最近 合并、最近插入、最远插入、最近添加、贪婪插入等)
(2)改进型的搜索算法
模拟退火算法
禁忌搜索算法
Hopfield神经网络优化算法
蚁群算法
遗传算法
混合优化策略
模拟退火算法(simulated annealing,SA)
是基于Monte Carlo迭代求解策略的一 种随机寻优算法,其出发点是基于物理中固体物质的退火过程与一般组合优化问题 之间的相似性。SA算法由某一较高初温开始,结合具有概率突跳特性的Metropolis 抽样策略在解空间中随机寻找目标函数的全局最优解,伴随温度参数的不断下降重 复抽样过程,最终得到问题的全局最优解。从算法结构知,新状态产生函数、新状 态接受函数、退温函数、抽样稳定准则和退火结束准则(简称三函数两准则)以及 初始温度是直接影响算法优化结果的主要环节。
禁忌搜索(Tabu Search或Taboo Search,简称TS)
是一种亚启发式搜索技术,由 Glover在1986年首次提出,进而形成一套完整算法。它是对局部邻域搜索的一种扩展, 是一种全局逐步寻优算法,是对人类智力过程的一种模拟。TS算法通过引入一种灵 活的存储结构和相应的禁忌准则来避免迂回搜索,并通过藐视准则来赦免一些被禁 忌的优良状态,进而保证多样化的有效探索以最终实现全局优化。简单TS算法的基 本思想是:给定一个当前解(初始解)和一种邻域,然后在当前解的邻域中确定若干 候选解,若最佳候选解对应的目标值优于“best so far”状态,则忽视其禁忌特性, 用其替代当前解和“best so far”状态,并将相应的对象加入禁忌表,同时修改禁忌 表中各对象的任期;若不存在上述候选解,则选择在候选解中选择非禁忌的最佳状 态为新的当前解,而无视它与当前解的优劣,同时将相应的对象加入禁忌表,并修 改禁忌表中各对象的任期;如此反复上述迭代搜索过程,直至满足停止准则。邻域 函数、禁忌对象、禁忌表和藐视准则,构成了禁忌搜索算法的关键。
Hopfield神经网络优化算法
就是利用神经网络中神经元的协同并行计算能力来 构造的优化算法,它将实际问题的优化解与神经网络的稳定状态相对应,把实际问 题的优化过程映射为神经网络系统的演化过程。Hopfield网络是典型的全连接网络, 通过在网络中引入能量函数以构造动力学系统,并使网络的平衡态与能量函数的极
小解相对应,从而将求解能量函数极小解的过程转化为网络向平衡态的演化过程。
蚁群算法
是一种新型的模拟进化算法,由意大利学者M. Dorigo、V. Maniezzo和 A. Colorini等人在90年代首先提出,称之为蚁群系统(ant colony system)。它是受到 人们对自然界中真实的蚁群集体行为的研究成果的启发而提出的一种基于种群的模 拟进化算法。生物学研究表明一群互相协作的蚂蚁能够找到食物源和巢之间的最短 路径,而单只蚂蚁则不能。蚂蚁间相互协作的方法是它们在在运动过程中,能够在 所经过的路径上留下一种称之为外激素的物质进行信息传递,而且蚂蚁在运动过程 中能够感知这种物质,并以此指导自己的运动方向,因此由大量蚂蚁组成的蚁群集 体行为便表现出一种信息正反馈现象:某一路径上走过的蚂蚁越多,则后来者选择该 路径的概率就越大。该算法已经成功地解决诸如TSP问题等多种组合优化问题,结果 可与模拟退火、遗传算法等通用的启发式算法相媲美。
遗传算法(Genetic Algorithms,简称GA)
是一种高度并行、随机和自适应的优 化算法,其基本思想是基于Darwin的进化论和Mendel的遗传学说。该算法最早由美 国密执安大学的教授于1975年创建,它将问题的求解表示成“染色体”的适者生存 过程,通过“染色体”群的一代代不断进化,包括复制、交叉和变异等操作,最终收 敛到“最适应环境”的个体,从而求得问题的最优解或满意解。通常遗传算法的设 计是按以下步骤进行的:①确定问题的编码方案;②确定适配置函数;③算法参数 的选取;④遗传算子的设计;⑤确定算法的终止条件。
近年来,
混合优化策略
得 到了较广泛的一个应用,并取得了理想的效果,其设计与分析已成为算法研究的一 个热点。例如利用遗传算法和模拟退火算法结合可以构造成的GA、SA混合优化策略, 这种混合不仅是算法结构上的,而且是搜索机制和进化思想上的相互补充,为较好 解决复杂优化问题提供了有力的途径。
算法比较:
模拟退火算法(SA)的实验性能具有质量高、初值鲁棒性强、通用易实现的优 点,最大缺点是往往优化过程较长,不太适合工业应用;遗传算法(GA)的两个最 显著的优点是隐含并行性和全局解空间搜索,但实际应用时易出现早熟收敛和收敛性 能差等缺点;禁忌搜索算法(TS)是一种局部搜索能力很强的全局迭代寻优算法,不 足之处在于对初始解较强的依赖性和串行的迭代搜索过程,在本问题中,要建立多 个轧制单元,串行的搜索策略效果不是很好;Hopfield神经网络优化算法具有简单、 规范、快速等优点,但是其优化性和鲁棒性比较差;蚁群算法(ACO)是一种本质 并行的算法,但其搜索时间比较长,也容易陷于局部最优解,使搜索停滞。
(3) n-opt法、贪婪算法、爬山法(HC法)、 回溯法、分支定界法、EP、混沌搜索、模糊优化等。这些方法在求解小规模TSP问 题上已经取得了一些成果。
(4)分散搜索算法
对于组合优化问题,分散搜索算法具有突出的求解能力,它通过保持参考集中的解分散性,将参考集中的部分解 进行组合后,用解改进算法开始新的搜索。这种搜索策略使得嵌入其中的解改进算 法尽量在足够大的解空间内搜索,搜索广泛性强。
参考论文:分散搜索算法在宝钢热轧一体化计划模型中的应用