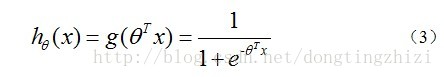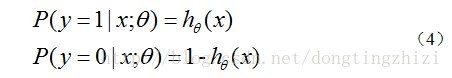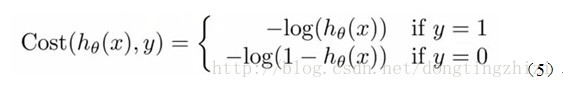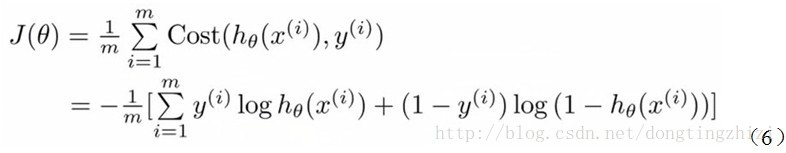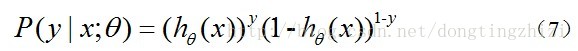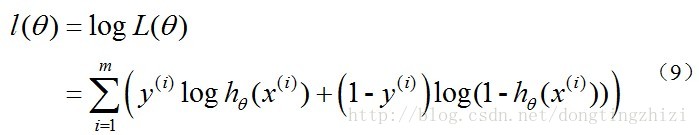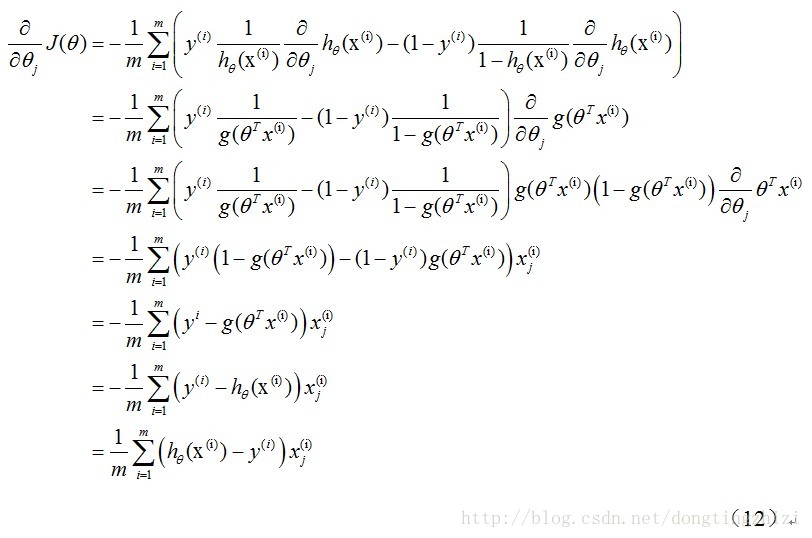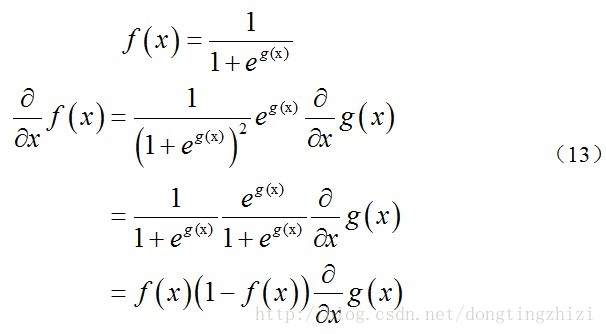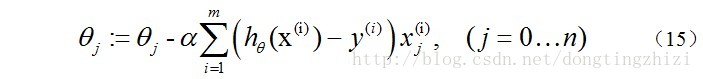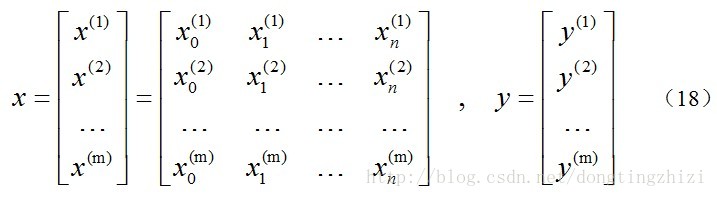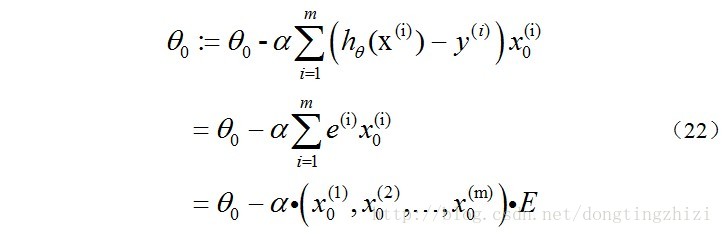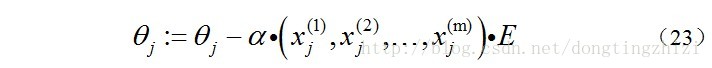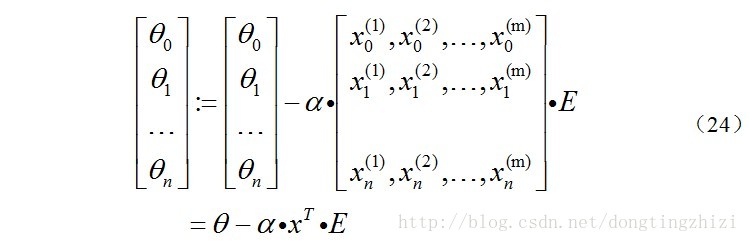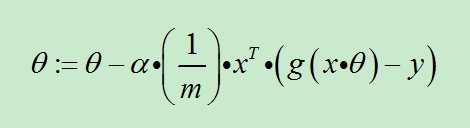(很多讲逻辑回归的文章都没有给出详细的推导,只是列出最后的计算公式,今天在网上看到一篇解释得非常详细的文章,赶紧转载一下:
【机器学习笔记1】Logistic回归总结
(http://blog.csdn.net/dongtingzhizi/article/details/15962797)
作者说”未经允许,不得转载”,我这里先冒犯了,如果觉得不合适,请告知。
)
Logistic回归总结
作者:洞庭之子
微博:
洞庭之子-Bing
(2013年11月)
PDF下载地址:
http://download.csdn.net/detail/lewsn2008/6547463
1.引言
看了Stanford的Andrew Ng老师的
机器学习
公开课中关于Logistic Regression的讲解,然后又看了《机器学习实战》中的LogisticRegression部分,写下此篇学习笔记总结一下。
首先说一下我的感受,《机器学习实战》一书在介绍原理的同时将全部的
算法
用源代码实现,非常具有操作性,可以加深对算法的理解,但是美中不足的是在原理上介绍的比较粗略,很多细节没有具体介绍。所以,对于没有基础的朋友(包括我)某些地方可能看的一头雾水,需要查阅相关资料进行了解。所以说,该书还是比较适合有基础的朋友。
本文主要介绍以下三个方面的内容:
(1)Logistic Regression的基本原理,分布在第二章中;
(2)Logistic Regression的具体过程,包括:选取预测函数,求解Cost函数和
J(θ)
,梯度下降法求
J(θ)
的最小值,以及递归下降过程的向量化(vectorization),分布在第三章中;
(3)对《机器学习实战》中给出的实现代码进行了分析,对阅读该书LogisticRegression部分遇到的疑惑进行了解释。没有基础的朋友在阅读该书的Logistic Regression部分时可能会觉得一头雾水,书中给出的代码很简单,但是怎么也跟书中介绍的理论联系不起来。也会有很多的疑问,比如:一般都是用梯度下降法求损失函数的最小值,为何这里用梯度上升法呢?书中说用梯度上升发,为何代码实现时没见到求梯度的代码呢?这些问题在第三章和第四章中都会得到解答。
文中参考或引用内容的出处列在最后的“参考文献”中。文中所阐述的内容仅仅是我个人的理解,如有错误或疏漏,欢迎大家批评指正。下面进入正题。
2. 基本原理
Logistic Regression和Linear Regression的原理是相似的,按照我自己的理解,可以简单的描述为这样的过程:
(1)找一个合适的预测函数(Andrew Ng的公开课中称为hypothesis),一般表示为
h
函数,该函数就是我们需要找的分类函数,它用来预测输入数据的判断结果。这个过程时非常关键的,需要对数据有一定的了解或分析,知道或者猜测预测函数的“大概”形式,比如是线性函数还是非线性函数。
(2)构造一个Cost函数(损失函数),该函数表示预测的输出(
h
)与训练数据类别(
y
)之间的偏差,可以是二者之间的差(
h-y
)或者是其他的形式。综合考虑所有训练数据的“损失”,将Cost求和或者求平均,记为
J(θ)
函数,表示所有训练数据预测值与实际类别的偏差。
(3)显然,
J(θ)
函数的值越小表示预测函数越准确(即
h
函数越准确),所以这一步需要做的是找到J(θ)函数的最小值。找函数的最小值有不同的方法,Logistic Regression实现时有的是梯度下降法(Gradient Descent)。
3. 具体过程
3.1 构造预测函数
Logistic Regression虽然名字里带“回归”,但是它实际上是一种分类方法,用于两分类问题(即输出只有两种)。根据第二章中的步骤,需要先找到一个预测函数(
h
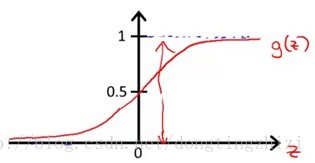
),显然,该函数的输出必须是两个值(分别代表两个类别),所以利用了Logistic函数(或称为Sigmoid函数),函数形式为:
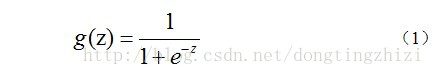
对应的函数图像是一个取值在0和1之间的S型曲线(图1)。
图1
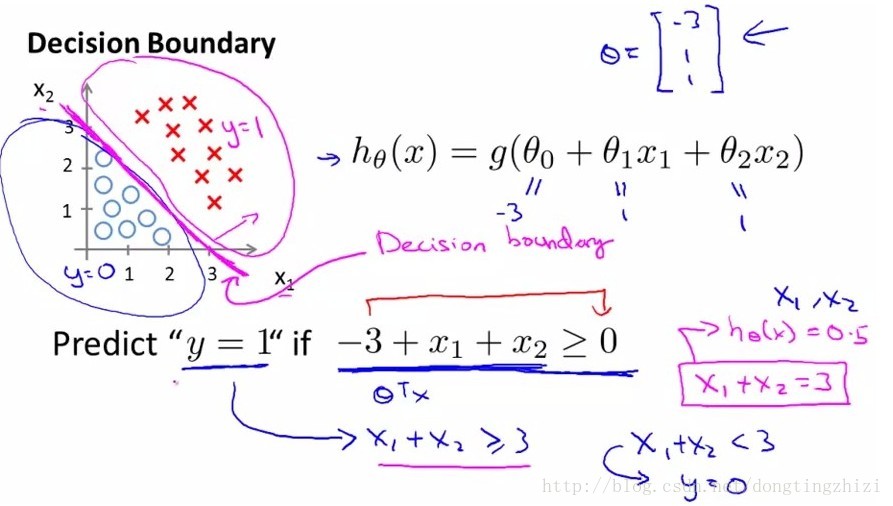
接下来需要确定数据划分的边界类型,对于图2和图3中的两种数据分布,显然图2需要一个线性的边界,而图3需要一个非线性的边界。接下来我们只讨论线性边界的情况。
图2
图3
对于线性边界的情况,边界形式如下:
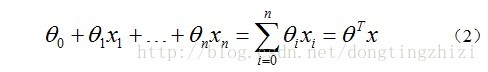
构造预测函数为:
hθ(x)
函数的值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
3.2 构造Cost函数
Andrew Ng在课程中直接给出了Cost函数及
J(θ)
函数如式(5)和(6),但是并没有给出具体的解释,只是说明了这个函数来衡量
h
函数预测的好坏是合理的。
实际上这里的Cost函数和
J(θ)
函数是基于
最大似然估计
推导得到的。下面详细说明推导的过程。(4)式综合起来可以写成:
取似然函数为:
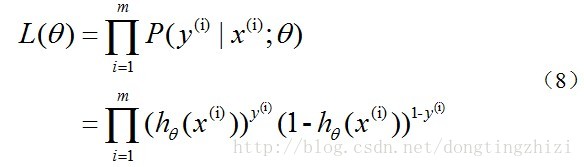
对数似然函数为:
最大似然估计就是要求得使
l(θ
)取最大值时的
θ
,其实这里可以使用梯度上升法求解,求得的
θ
就是要求的最佳参数。但是,在Andrew Ng的课程中将
J(θ)
取为(6)式,即:
因为乘了一个负的系数
-1/m
,所以
J(θ)
取最小值时的
θ
为要求的最佳参数。
3.3 梯度下降法求
J(θ)
的最小值
求
J(θ)
的最小值可以使用梯度下降法,根据梯度下降法可得
θ
的更新过程:
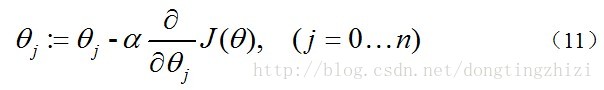
式中为
α
学习步长,下面来求偏导:
上式求解过程中用到如下的公式:
因此,(11)式的更新过程可以写成:
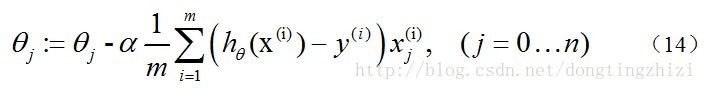
因为式中
α
本来为一常量,所以
1/m
一般将省略,所以最终的
θ
更新过程为:
另外,补充一下,3.2节中提到求得
l(θ
)
取最大值时的
θ
也是一样的,用梯度上升法求(9)式的最大值,可得:
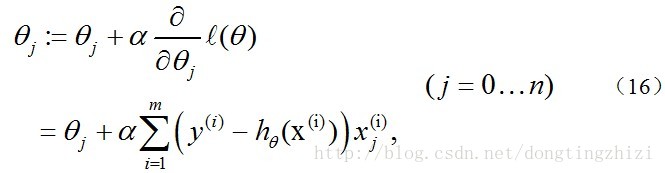
观察上式发现跟(14)是一样的,所以,采用梯度上升发和梯度下降法是完全一样的,这也是《机器学习实战》中采用梯度上升法的原因。
3.4 梯度下降过程向量化
关于
θ
更新过程的vectorization,Andrew Ng的课程中只是一带而过,没有具体的讲解。
《机器学习实战》连Cost函数及求梯度等都没有说明,所以更不可能说明vectorization了。但是,其中给出的实现代码确是实现了vectorization的,图4所示代码的32行中weights(也就是
θ
)的更新只用了一行代码,直接通过矩阵或者向量计算更新,没有用for循环,说明确实实现了vectorization,具体代码下一章分析。
文献[3]中也提到了vectorization,但是也是比较粗略,很简单的给出vectorization的结果为:
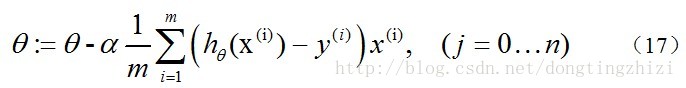
且不论该更新公式正确与否,这里的
Σ(…)
是一个求和的过程,显然需要一个for语句循环m次,所以根本没有完全的实现vectorization,不像《机器学习实战》的代码中一条语句就可以完成
θ
的更新。
下面说明一下我理解《机器学习实战》中代码实现的vectorization过程。
约定训练数据的矩阵形式如下,
x
的每一行为一条训练样本,而每一列为不同的特称取值:
约定待求的参数
θ
的矩阵形式为:
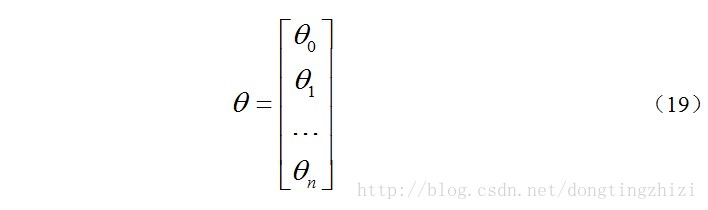
先求
x.θ
并记为
A
:
求
hθ(x)-y
并记为
E
:
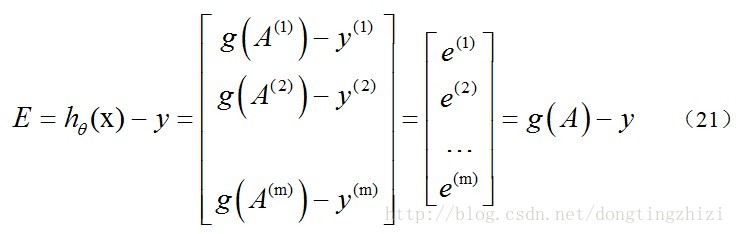
g(A)
的参数
A
为一列向量,所以实现
g
函数时要支持列向量作为参数,并返回列向量。由上式可知
hθ(x)-y
可以由
g(A)-y
一次计算求得。
再来看一下(15)式的
θ
更新过程,当
j=0
时:
同样的可以写出
θj
,
综合起来就是:
综上所述,vectorization后
θ
更新的步骤如下:
(1)求
A=x.θ
;
(2)求
E=g(A)-y
;
(3)求
θ:=θ-α.x’.E,
x’表示矩阵x的转置。
也可以综合起来写成:
前面已经提到过:1/m是可以省略的。
4. 代码分析
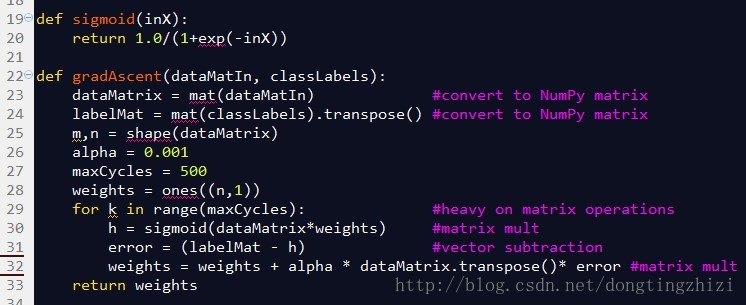
图4中是《机器学习实战》中给出的部分实现代码。
图4
sigmoid函数就是前文中的
g(z)
函数,参数
inX
可以是向量,因为程序中使用了
Python
的numpy。
gradAscent函数是梯度上升的实现函数,参数dataMatin和classLabels为训练数据,23和24行对训练数据做了处理,转换成numpy的矩阵类型,同时将横向量的classlabels转换成列向量labelMat,此时的dataMatrix和labelMat就是(18)式中的
x
和
y
。alpha为学习步长,maxCycles为迭代次数。weights为n维(等于
x
的列数)列向量,就是(19)式中的
θ
。
29行的for循环将更新
θ
的过程迭代maxCycles次,每循环一次更新一次。对比3.4节最后总结的向量化的
θ
更新步骤,30行相当于求了
A=x.θ
和
g(A)
,31行相当于求了
E=g(A)-y
,32行相当于求
θ:=θ-α.x’.E
。所以这三行代码实际上与向量化的
θ
更新步骤是完全一致的。
总结一下,从上面代码分析可以看出,虽然只有十多行的代码,但是里面却隐含了太多的细节,如果没有相关基础确实是非常难以理解的。相信完整的阅读了本文,就应该没有问题了!^_^。
【参考文献】
[1]《机器学习实战》——【美】Peter Harington
[2] Stanford机器学习公开课(
https://www.coursera.org/course/ml
)
[3]
http://blog.csdn.net/abcjennifer/article/details/7716281
[4]
http://www.cnblogs.com/tornadomeet/p/3395593.html
[5]
http://blog.csdn.net/moodytong/article/details/9731283
[6]
http://blog.csdn.net/jackie_zhu/article/details/8895270