pytorch批标准化
In continuation of my previous
post
, in this post we will discuss about “Batch Normalisation” and its implementation in PyTorch.
在我之前的
文章的
继续中,我们将在本文中讨论“批处理规范化”及其在PyTorch中的实现。
Batch normalisation is a mechanism that is used to improve efficiency of neural networks. It works by stabilising the distributions of hidden layer inputs and thus improving the training speed.
批处理规范化是一种用于提高神经网络效率的机制。 它通过稳定隐藏层输入的分布来工作,从而提高了训练速度。
1.批量归一化的本质
(
1. Essence of Batch Normalisation
)
In neural networks, inputs to each layer are affected by the parameters of all preceding layers and changes to the network parameters amplify as the network becomes deeper. During training of neural networks, weights get updated due to mechanism of backpropagation. Thus, training of neural networks becomes difficult as the the distribution of each layer’s inputs change while training.
These changes in the distribution of internal nodes of deep neural network are termed as Internal Covariate Shift.
在神经网络中,每层的输入都受所有先前层的参数的影响,并且随着网络的深入,对网络参数的更改也会放大。 在神经网络的训练过程中,权重由于反向传播的机制而更新。 因此,随着训练过程中每一层输入的分布发生变化,训练神经网络变得困难。
深度神经网络内部节点分布中的这些变化称为内部协变量平移。
Internal Covariate Shift is defined as the change in the distribution of network activations due to the change in network parameters during training.
内部协变量移位定义为由于训练过程中网络参数的变化而导致的网络激活分布的变化。
什么是批量标准化?
(
What Batch Normalisation does ?
)
Batch Normalisation tends to fix the distribution of the hidden layer values as the training progresses. It makes sure that the values of hidden units have standardised mean and variance .
随着训练的进行,批次归一化倾向于固定隐藏层值的分布。 它可以确保隐藏单位的值具有标准化的均值和方差。
批次归一化如何解决内部协变量偏移?
(
How Batch Normalisation fixes Internal Covariate Shift ?
)
It accomplishes this via a normalisation step that fixes the means and variances of layer inputs.
它通过固定图层输入的均值和方差的归一化步骤来完成此操作。
Let’s deep dive into this process:-
让我们深入研究这个过程:

Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
批次标准化:通过减少内部协变量偏移来加速深度网络训练
Explanation:-
说明:-
-
Calculates mean(
µ
) of x channel in batch (batch size
m)
(hence
Batch
Normalisation).计算批次(批次大小
m
)中x通道的平均值(
µ
)(因此进行
批次
归一化)。 -
Calculates variance
(σ2)
of x channel in batch (batch size
m)
.批量计算x通道(批量大小
m)的
方差
(σ2
)
。 -
mean(
µ
) is subtracted from the channel value followed by division with square-root of sum of channel variance(
σ2
) and
ε
(to handle divide by zero) .从通道值中减去均值(
µ
),然后除以通道方差(
σ2
)和
ε
之和的平方根(以除以零)。
At this point, transformed channel values have zero mean and unit variance.
此时,转换后的通道值的均值和单位方差为零。
-
Above value obtained is multiplied by gamma(
γ
) (scale operation) followed by addition of Beta (
β
) (shift operation).
By using γ and β , the original activation can be restored.
将获得的上述值乘以gamma(
γ
)(标度运算),然后再加上Beta(
β
)(移位运算)。
通过使用γ和β,可以恢复原始激活。
For each channel , two trainable(γ and β) and two non-trainable parameters (µ and σ2) are added to the network.
对于每个通道,将两个可训练参数(γ和β)和两个不可训练参数(μ和σ2)添加到网络。
Why Beta and Gamma have been introduced?
为什么引入Beta和Gamma?
The network training converges faster if its inputs are whitened i.e. linearly transformed to have zero means and unit variances. While it’s not always necessary that zero mean and unit variance for the hidden layer values is best, there are chances that any other distribution might be better too.
如果网络训练的输入被白化(即线性变换为零均值和单位方差),则网络训练收敛更快。 虽然不一定总是使隐藏层值的零均值和单位方差最佳,但其他分布也可能会更好。
To address this, we make sure that the transformation inserted in the network can represent the identity transform( by introducing γ and β — which scale and shift the normalised value). We can make sure hidden units have standardised mean and variance where mean and variance are controlled by two explicit trainable parameters γ and β .
为了解决这个问题,我们确保插入到网络中的变换可以表示身份变换(通过引入γ和β-缩放和移动归一化值)。 我们可以确保隐藏单元具有标准化的均值和方差,其中均值和方差由两个显式可训练参数γ和β控制。
Deep neural nets can be trained faster and generalize better when the distribution of activations is kept normalised during BackPropagation.
在BackPropagation期间,将激活的分布保持标准化时,可以更快地训练深度神经网络并更好地推广。
2.在PyTorch中进行批量归一化
(
2. Batch Normalisation in PyTorch
)
Using
torch.nn.BatchNorm2d ,
we can implement Batch Normalisation. It takes input as
num_features
which is equal to the number of out-channels of the layer above it.
使用
torch.nn.BatchNorm2d,
我们可以实现批量标准化。 它以
num_features
作为输入,该输入等于其上一层的出通道数量。
Let’s understand impact of Batch Normalisation by considering two neural networks, one with Batch-Norm and other without Batch-Norm layers.
让我们通过考虑两个神经网络来理解批处理规范化的影响,其中一个具有Batch-Norm,另一个不具有Batch-Norm层。
a)解释模型摘要
(
a) Interpreting Model Summary
)
-
Model 1 — without Batch-Norm
模型1 —不使用批量范本

-
Model 2- with Batch-Norm layers.
具有批处理标称层的模型2。
I have updated Model 1 network by adding BatchNorm layers between Convolution layer and RELU to construct Model -2.
我通过在卷积层和RELU之间添加BatchNorm层来构建Model -2,从而更新了Model 1网络。
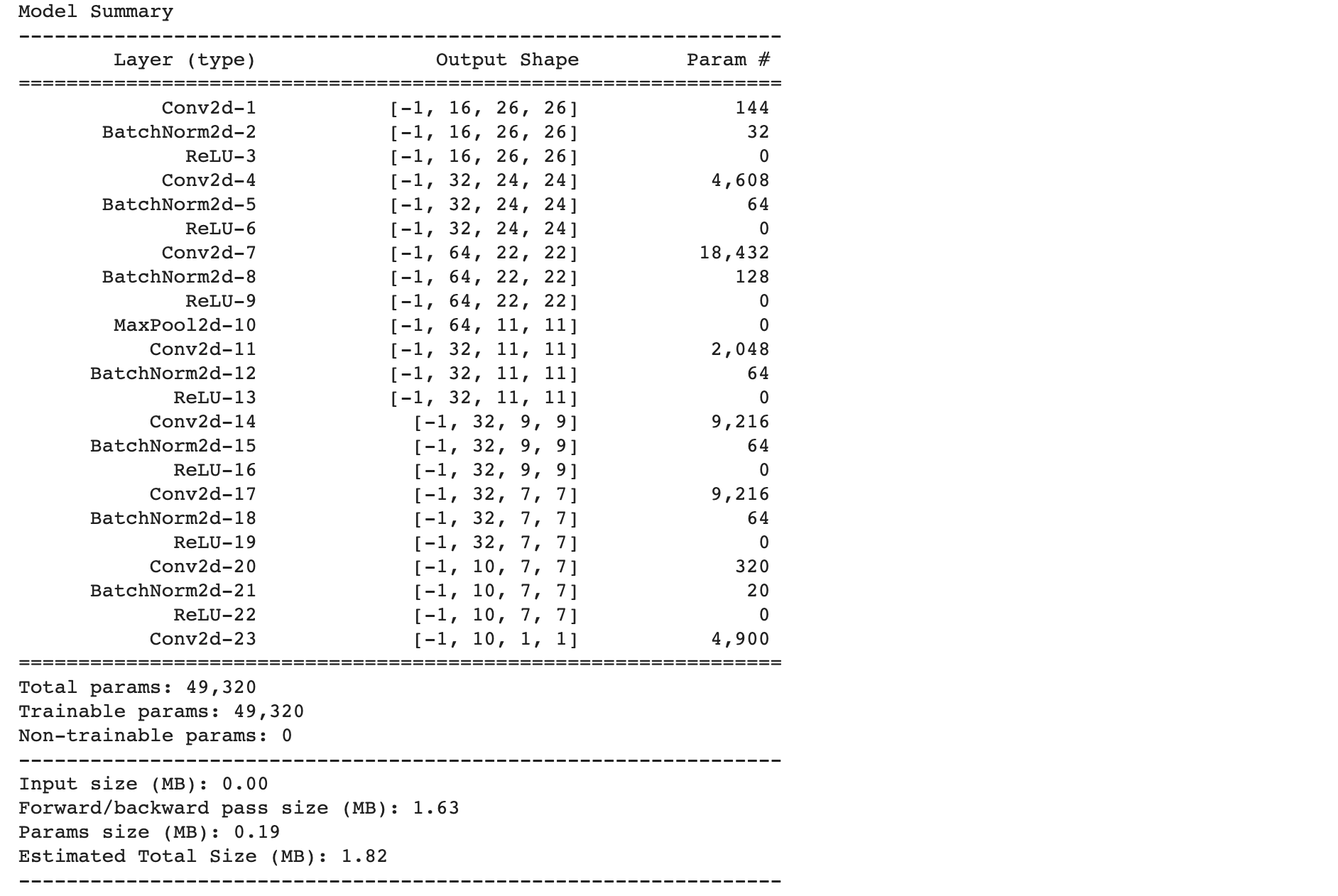
推论:
(
Inferences:-
)
-
Increase in number of trainable parameters on adding Batch-Norm layer. Earlier we had 48.8k parameters after adding multiple Batch-Norm layers we have 49.3k parameters .
添加批处理标准层时,可训练参数的数量增加。 在添加多个Batch-Norm层后,我们有48.8k的参数,我们有49.3k的参数。
-
For each Batch-Norm layer, you can notice number of parameters are double the number of output channels. Eg. For layer BatchNorm2d-2 , there are 16 output channels hence corresponding to that trainable parameters are 32(gammas and betas).
对于每个批处理规范层,您可以注意到参数数量是输出通道数量的两倍。 例如。 对于层BatchNorm2d-2,有16个输出通道,因此对应的可训练参数为32(游戏和测试版)。
-
For Batch-Norm layer, you can notice input shape and output shape both are same.
对于Batch-Norm层,您会注意到输入形状和输出形状都相同。
b)模型的效率和速度
(
b) Model efficiency and speed
)
For both above shown networks (with and without Batch Normalisation) , I ran 10 epochs for MNIST dataset.
对于以上显示的两个网络(使用和不使用批次归一化),我都为MNIST数据集运行了10个纪元。
-
Model 1- without Batch-Norm
1型-不使用批量范本

-
Model 2- with Batch-Norm
带有批处理标称的模型2-

推理:-
(
Inference:-
)
-
On comparing final accuracies in the last epoch(10th) , without Batch-Norm model reached 98.75% train accuracy and 98.4% test accuracy whereas with Batch-Norm model has 99.92% train accuracy and 99.39% test accuracy.
在比较最后一个时期(第10个)的最终精度时,没有批处理标准模型的训练精度为98.75%,测试精度为98.4%,而使用批处理标准模型的训练精度为99.92%,测试精度为99.39%。
By using Batch-Norm, model trains faster and it’s capacity is also higher.The point to be noted here is with Batch Normalisation we can increase the model capacity
in fewer training steps
as compared to without Batch-Norm model hence making model learn faster. While there is need to mend overfitting (for the examples taken here), which we will discuss in coming posts.
通过使用批量规范,模型火车速度更快,它的能力也是这里要注意点较高。与批标准化与没有因此批量规范模型制作模型学习得更快,我们可以增加模型容量
较少的训练步骤
。 尽管需要修复过度拟合(此处示例),但我们将在以后的文章中进行讨论。
There is an option to turn off these learnable parameters by setting
affine=False,
by default it is set to True. There is a debate on whether Batch-Norm should be used before RELU or after. In this example I have used it before RELU layer.
可以通过设置
affine = False
来关闭这些可学习的参数
,
默认情况下将其设置为True。 关于是否应在RELU之前或之后使用Batch-Norm,存在争议。 在此示例中,我在RELU层之前使用了它。
You can find the corresponding codes for with and without Batch-Norm layer models in
this
repository.
您可以在
此
存储库中找到带有或不带有Batch-Norm层模型的相应代码。
翻译自:
https://medium.com/analytics-vidhya/exploring-batch-normalisation-with-pytorch-1ac25229acaf
pytorch批标准化