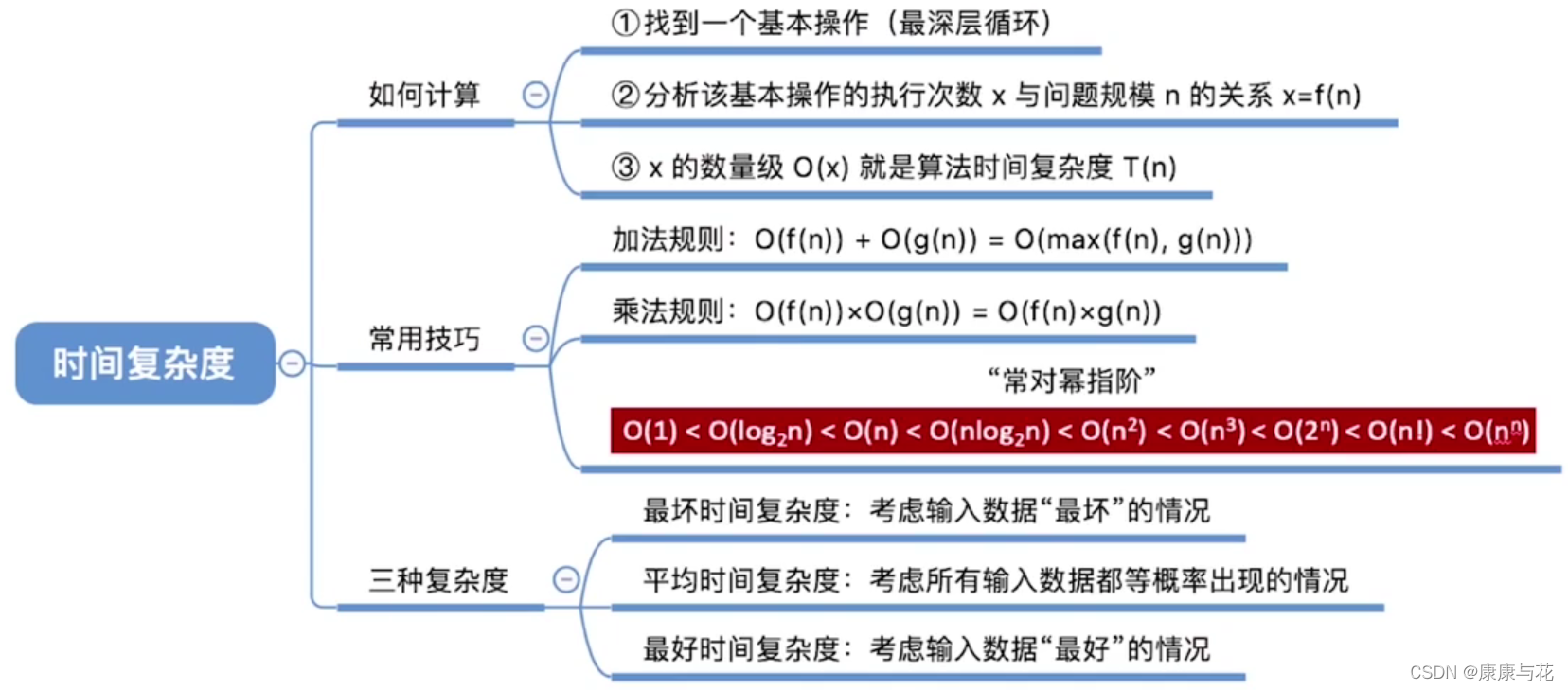
一.如何计算

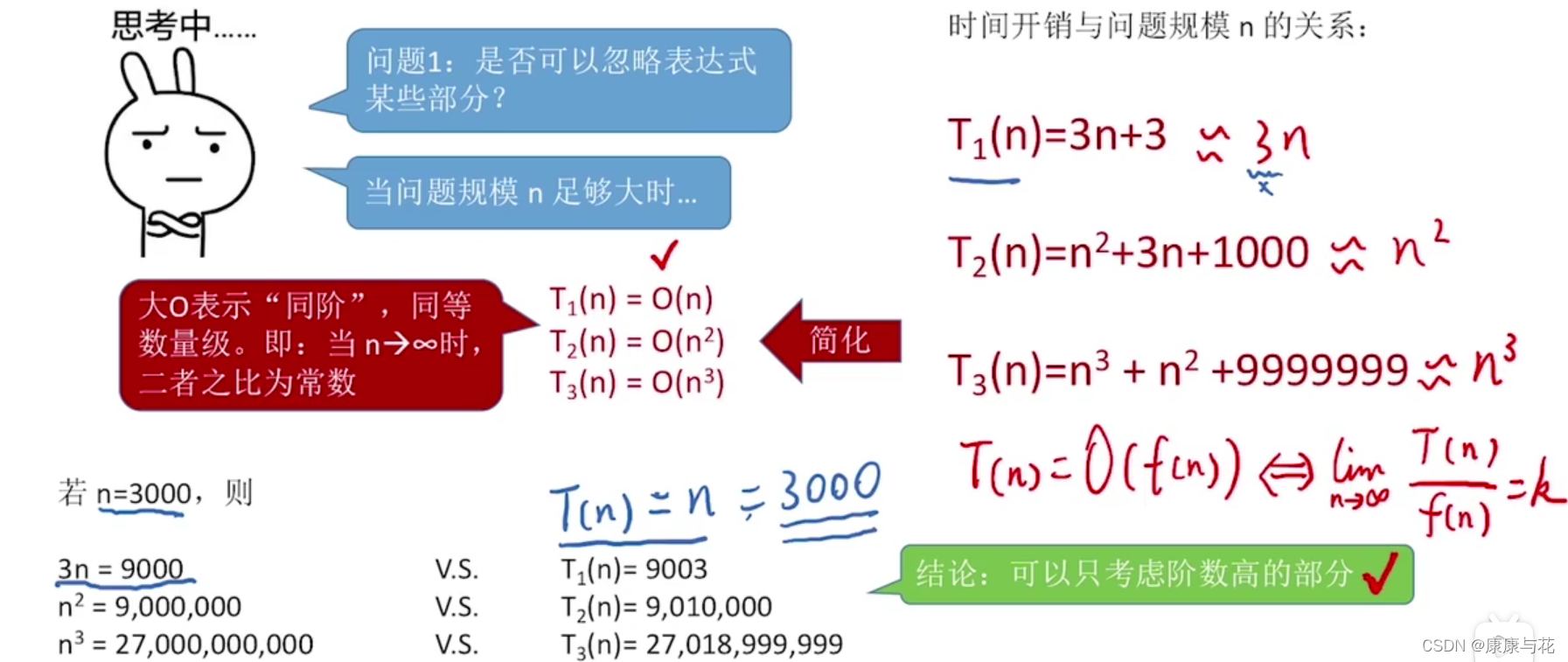
1.时间复杂度是总运算次数表达式中受n的变化影响最大的那一项(不含系数)

一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。

一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

2.一般情况下，算法的基本操作重复执行的次数是模块n的某一个函数f（n），因此，算法的时间复杂度记做：T（n）=O（f（n））。随着模块n的增大，算法执行的时间的增长率和f（n）的增长率成正比，所以f（n）越小，算法的时间复杂度越低，算法的效率越高。

在计算时间复杂度的时候，先找出算法的基本操作，然后根据相应的各语句确定它的执行次数，再找出T（n）的同数量级（它的同数量级有以下：1，Log2n ，n ，nLog2n ，n的平方，n的三次方，2的n次方，n！），找出后，f（n）=该数量级，若T(n)/f(n)求极限可得到一常数c，则时间复杂度T（n）=O（f（n））。

3.常见的时间复杂度

按数量级递增排列，常见的时间复杂度有：常数阶O(1),  对数阶O(log2n),  线性阶O(n),  线性对数阶O(nlog2n),  平方阶O(n^2)， 立方阶O(n^3),...， k次方阶O(n^k), 指数阶O(2^n) 。其中，
1.O(n)，O(n^2)， 立方阶O(n^3),...， k次方阶O(n^k) 为多项式阶时间复杂度，分别称为一阶时间复杂度，二阶时间复杂度。。。。

2.O(2^n)，指数阶时间复杂度，该种不实用。

3.对数阶O(log2n),   线性对数阶O(nlog2n)，除了常数阶以外，该种效率最高。

一个问题本身也有它的复杂性，如果某个算法的复杂性到达了这个问题复杂性的下界，那就称这样的算法是最佳算法。

二.常用技巧

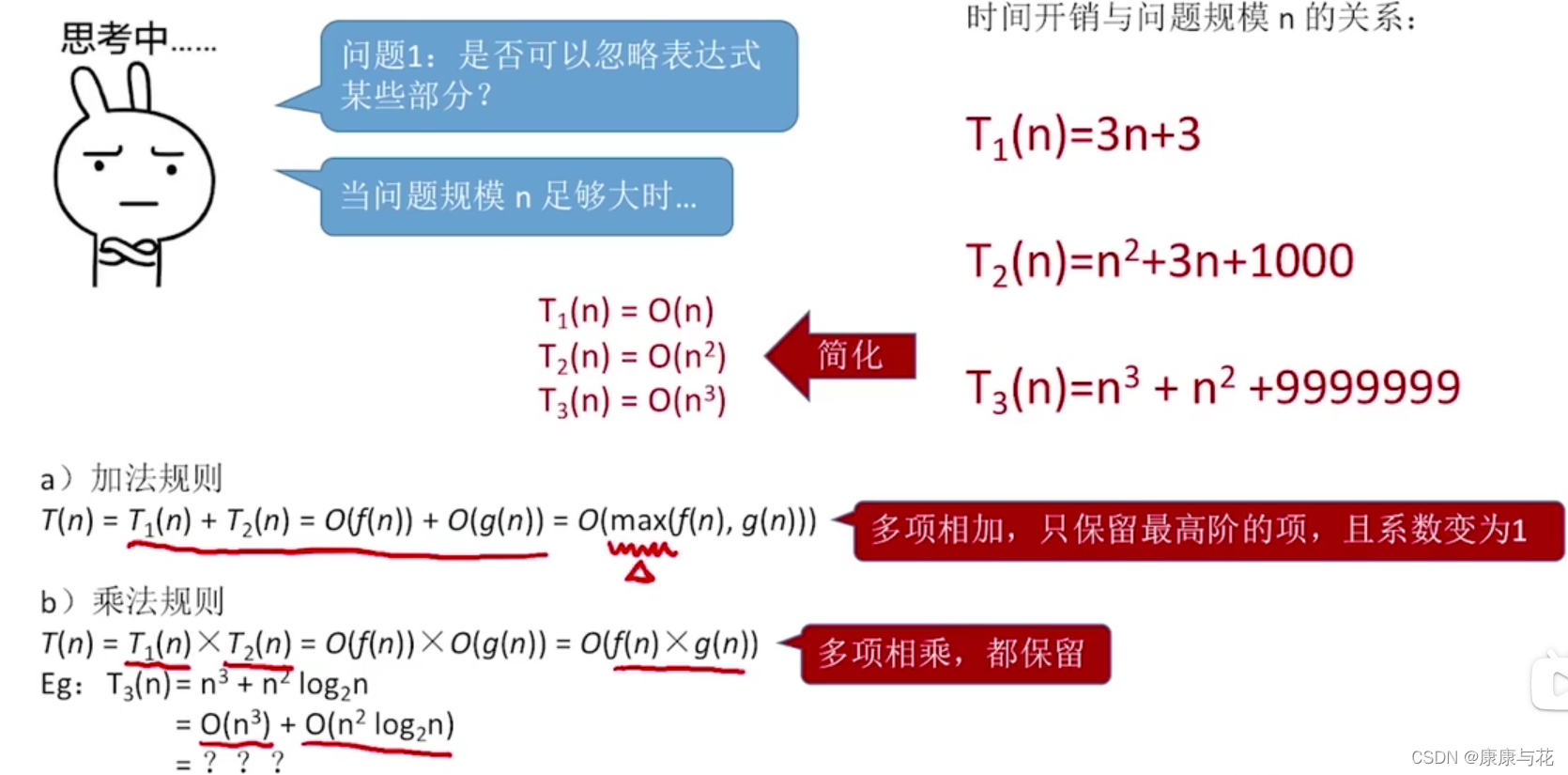
1. 时间复杂度的几条基本计算规则


基本操作

，即只有常数项，认为其时间复杂度为O(1)


顺序结构

，时间复杂度按加法进行计算


循环结构

，时间复杂度按乘法进行计算


分支结构

，时间复杂度取最大值

判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略

在没有特殊说明时，我们所分析的算法的时间复杂度都是指


最坏时间复杂度.

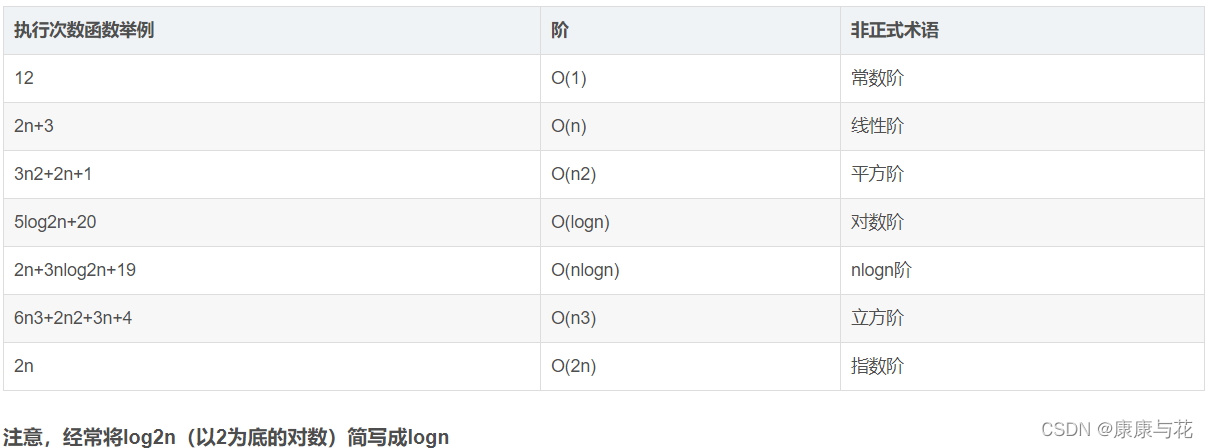
结论一：顺序执行的代码只会影响常数项，可以忽略。    顺序执行指没有循环的代码，每行代码都是不同的。

结论二：只需挑循环中的一个基本操作分析它的执行次数与n的关系即可。

结论三：如果有多层循环嵌套，只需关注最深层循环循环了几次。

三.三种复杂度

1. 分析算法时，存在几种可能的考虑：


算法完成工作最少需要多少基本操作，即

最优时间复杂度


算法完成工作最多需要多少基本操作，即

最坏时间复杂度


算法完成工作平均需要多少基本操作，即

平均时间复杂度


对于最优时间复杂度，其价值不大，因为它没有提供什么有用信息，其反映的只是最乐观最理想的情况，没有参考价值。

对于平均时间复杂度，是对算法的一个全面评价，因此它完整全面的反映了这个算法的性质。但另一方面，这种衡量并没有保证，不是每个计算都能在这个基本操作内完成。而且，对于平均情况的计算，也会因为应用算法的实例分布可能并不均匀而难以计算。

对于最坏时间复杂度，提供了一种保证，表明算法在此种程度的基本操作中一定能完成工作。

因此，我们主要关注算法的最坏情况，亦即最坏时间复杂度。

小结：