logn是什么意思_二进制究竟有什么用？带你看看那些好玩儿的位操作

(给算法爱好者加星标，修炼编程内功)

来源：小齐本齐

计算机说到底就是 0 和 1，所有的数在内存中都是以二进制的形式储存的。

而位操作，或者说位运算，就是直接对内存中的二进制位进行操作。

位运算可以说是我们的基本功，今天这篇文章就从以下角度和大家一起玩转位运算。

位运算究竟有什么用？
原码反码补码
7

种位运算

当然了，位运算还有很多奇技淫巧，如果大家还想看进阶篇，记得给我

点赞

或者

留言

告诉我哦～

位运算的作用

在实际生产中，位运算是用来

优化时间和空间

的。

位运算可能并不会降低复杂度的等级，但是可以把复杂度前面的系数降下来。

举个例子。

大家都知道堆，或者叫优先队列，一般来说是用

完全二叉树

来实现的，叫做

二叉堆

。

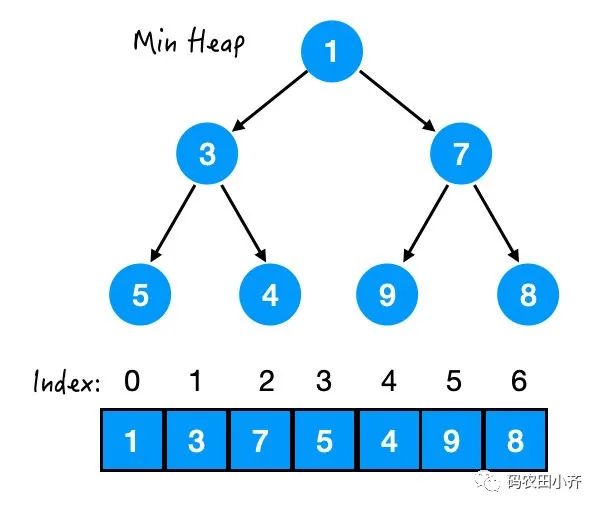
二叉堆插入、删除元素的时间复杂度都是
O(logn)
，如果这个不清楚的同学赶紧在公众号内回复「

堆

」复习一下，或者点击这里～

但是有另一种堆，它能够做到
O(1)
的时间插入元素，
O(logn)
的时间删除元素，我在堆这篇文章里也提到过，就是

斐波那契堆

。

但为什么不用呢？

就是因为 O(1) 前面的系数非常大。

我们说
O(logn)
比
O(1)
好，是有个条件的，那就是
n
非常非常大的情况下，但是实际上，如果
n
是在
int
范围内，那么取个
log
也不过就是
32
了，反而这个
O(1)
的时间复杂度可能系数达到几百几千。

一般来说实际应用中时间的测量并不是像我们做算法题时用时间复杂度这么简单，有的时候就需要你把两个算法都实现出来，去跑去测量它的时间，才能决定哪个好。

那么二进制一次能够作用于 32 位上(假设是一个 int)，如果数据表示的巧妙，这完全可以优化 32 倍，多用几个 int 就多优化了好几个 32 倍，不香吗？

除了优化时间，还可以优化空间。

比如在网站发布新版本时，一般都会附上支持该版本的浏览器列表，不然有些老掉牙的浏览器看不到我的新功能还算我的锅么？

那么怎么有效的表示这个浏览器列表呢？

全世界所有浏览器都有个国际标准编号，这里我就简单假设一下：

0 表示 QQ 浏览器
1 表示 Chrome 浏览器
2 表示火狐浏览器
3 表示 …

那么我们就可以用一个
int
表示是否支持这些浏览器的状态，如果这个浏览器能用，那么这一位上就设为 1，不能用就设为 0，这样用一个
int
就能表示 32 个网站。

那么国内的某个网站可以表示为：

0b …. 1101

所以位操作在很多代码里都很常用，比如网络协议、操作系统等等。

这就是位运算的两大优势，接下来我们说说具体的知识点。

原码反码补码

数字有正有负，Java 中用的是
signed type
，就是有正有负的。

虽然在
Java 8
之后，也用了个工具来实现
unsigned type
，但是其实底层实现是没有的。

二进制最左边的一位是符号位，

0 表示这个数是非负数；
1 表示这个数是负数。

对了，最左边的一位英文叫做

most significant bit

，别说错了。。。

正数

正数的原码反码补码相同，没啥好说的。

比如：

int 1 = 0b 0000 0000 0000 0001
int 2 = 0b 0000 0000 0000 0010

负数：

原码

：把相应的正数的符号位设为 1。

-1 的原码 = 0b 1000 0000 0000 0001
-2 的原码 = 0b 1000 0000 0000 0010

反码 ones’ complement

：

符号位是 1，其余位取反。

-1 的反码 = 0b 1111 1111 1111 1110
-2 的反码 = 0b 1111 1111 1111 1101

补码 two’s complement

：

反码 + 1。

-1 的补码 = 0b 1111 1111 1111 1111
-2 的补码 = 0b 1111 1111 1111 1110

而计算机中真正用来存储数据的是用

补码

。

这里稍微注意下反码和补码的英文，
ones'
的这个
'
在后面，
two's
的这个
'
在中间。。

为什么计算机要用补码来存储数据呢？

可能有同学会说正零负零的原因，但这只是表面现象。

实际上通过补码这样精巧的设计，计算机做加减乘除运算就不用考虑符号，就可以让硬件里 CPU 的设计变得异常简单。

最初计算机只有加法器没有减法器，所以它用这么一种方式用加法完成了减法。

int 的最大值是多少？

正是因为最左边一位是符号位，所以正数的表示就少了一位能用的，那么 int 的最大值就是：

0111111…11 (31 ones) = 2^31 – 1 = 2147483647

7 种位运算

运算符	中文	英文	运算规则
<<	左移	left shift	右边补充 0
>>	右移	signed right shift	左边补充符号位
>>>	无符号右移	unsighed right shift	Java 特有，左边补充 0
~	位非	NOT	每位取反
&	位与	bitwise AND	每位做与操作，都是 1 则为 1，否则为 0
I	位或	OR	每一位做或操作，有 1 则为 1，否则为 0
^	异或	XOR	相同为 0，不同为 1

要注意的是前 4 个运算符是对 1 个数进行操作的，且操作完成后这个数本身的值不变(与 i++ 不同)；后 3 个操作是两个数的运算。

我们一一来看。

为了书写方便，下面的数值虽然是 int 类型，但我只写 8 位，大家都能理解的噢！

1. <<

左移操作就是把这些零啊壹啊的整体往左移动 n 位，右边缺的就补充 0。

1 = 0b 0000 0001
1 << 1 = 0b 0000 0010 = 2
2 = 0b 0000 0010
2 << 1 = 0b 0000 0100 = 4
3 = 0b 0000 0011
3 << 1 = 0b 0000 0110 = 6

诶，大家发现没有，左移 1 位之后这个数相当于

乘2

。

但是这只适用于左边溢出的高位中

不包含 1

时。

如果把 1 扔了，那就肯定不是 2 倍了嘛。

2. >>

右移操作就是整体往右移动 n 位，左边缺的补充符号位。

1 = 0b 0000 0001
1 >> 1 = 0b 0000 0000 = 0
2 = 0b 0000 0010
2 >> 1 = 0b 0000 0001 = 1
3 = 0b 0000 0011
3 >> 1 = 0b 0000 0001 = 1

同理，正数右移操作的效果是这个数

除以 2

。

如果是负数呢？

-3 = 1111 1101
-3 >> 1 = 1111 1110 = -2

因为 Java 是向零取整，所以

奇数

时会有问题，就不再是除以 2 的结果。

总结一下，

对于非负数、负数且是偶数，右移一位与除以 2 结果一样；
对于负数且是奇数，右移一位不等于除以2。

3. >>>

和 >> 的不同之处在于，这个的左边空缺的不论正负，一律补充 0。

所以对于正数来说，和 >> 的效果一样，但是负数不同。

-3 = 1111 1101
-3 >> 1 = 01111 1110 = 很大的数。。

4. ～

取反操作，就是每一位取反，1变成0，0变成1。

3 = 0b 0000 0011
~3 = 0b 1111 1100

5. &

这个符号其实和逻辑与运算 && 意思一样，只不过作用在每一位上。

对于每一位来说，两个数都是真，则为真，否则为假。

3 = 0b 0000 0011
5 = 0b 0000 0101
3&5 = 0b 0000 0001

6. |

同理，和逻辑或运算 || 意思一样，只不过作用在每一位上。

对于每一位来说，但凡有个真的就是真，否则为假。

3 = 0b 0000 0011
5 = 0b 0000 0101
3|5 = 0b 0000 0111

7. ^

最后一个异或操作，相同为 0，不同为 1。

3 = 0b 0000 0011
5 = 0b 0000 0101
3^5 = 0b 0000 0110

好啦，以上就是位运算的基本操作了，由这些运算做些巧妙的组合还可以得到很多有趣的结果，大家喜欢的话记得点赞评论哦～

– EOF –