演化博弈
演化博弈论不同于传统的经典博弈论,它是将演化的思想和博弈论进行结合,其中演化思想最初来自于生物学领域,达尔文认为生物界的发展就是一个不断演化的过程。20世纪末兴起的演化经济学思想,就是把达尔文在生物界所提到的“变异,选择和遗传”的过程转化为“创新,选择和扩散”的过程。演化经济学的思想更加强调了经济社会系统具有相当复杂的特征,它突破了传统西方经济学的思想,运用生物学科这个系统来研究整个经济社会。在当前全球化时代下,各国对资本展开激烈竞争所产生的各类社会问题,本身也是一个复杂的过程,因此运用演化的思想来分析更加的合理。演化博弈论和演化经济学都把“创新,选择和扩散”视为演化的主要机制,演化博弈论也为演化经济学提供了微观基础,演化博弈的基本形成如下图:
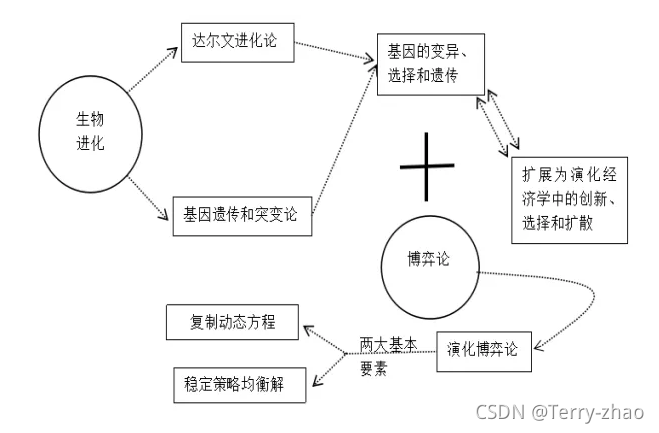
演化博弈把支付函数转为适应度函数,整个演化过程遵循选择机制和变异机制,选择机制即为通过演化博弈矩阵来确定复制动态方程,并求出包含的解,变异机制是用来检验演化均衡是否是稳定的,即验证复制动态方程所求出的解是否是演化稳定策略解。
演化博弈模型中,所构建的复制动态方程的基本形式为:

式子中各字母的含义如下:
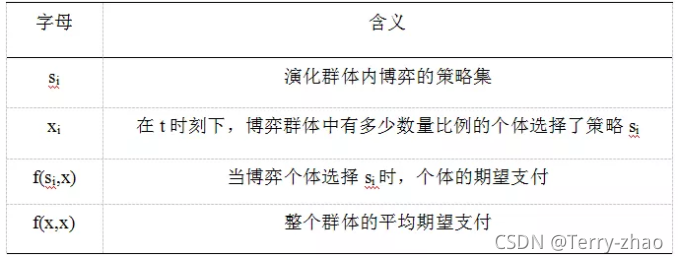
在演化博弈过程中,博弈双方不再是以稳定的纳什均衡解作为策略最终的选择结构,而是通过一个不断比较、学习和模仿的过程,逐渐去探究演化稳定均衡解,演化博弈模型的基本形式如下:(在下表博弈矩阵中,P1策略博弈主体的数量比例为x,P2策略博弈主体的数量比例为1-x)
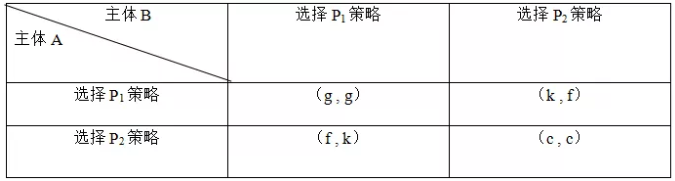
在上述博弈矩阵中各字母的表示含义如下:
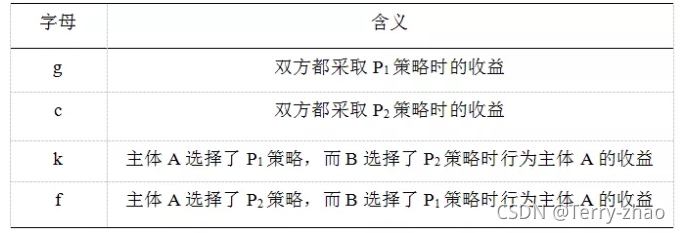
因此行为主体A(用U1代表)和行为主体B(用U2代表)各自的收益以及整个博弈群体的平均收益(用U代表)满足以下等式。

根据演化博弈概念,构建演化博弈的复制动态方程,即F(x)=dx/dt=x(U1-U),通过数理计算可以得出复制动态方程的最终形式为:F(x)=x(1-x)[k-f+x(g-f-k+c)],令复制动态方程结果为零,得出x1=0,x2=1,x3=(c-k)/(g-f-k+c)这三个解,再将这三个解入公式F’(x)中,即复制动态方程的一阶导方程中。若F’(x)<0,则该解就是演化博弈的稳定策略均衡解。