1:、三相电压空间矢量的合成
设直流母线侧电压为Udc,逆变器输出的三相相电压为UA、UB、UC、其分别加在空间上互差120°的三相静止平面坐标系上,可以定义三个相电压UA(t)、UB(t)、UC(t)、他们的方向始终在各自的轴线上,而大小随着时间按正弦规律变换,时间相位互差120°。假设Um为相电压幅值,f为频率,则有:
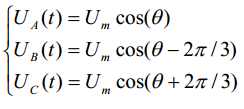
其中,θ=2πft,则三相空间电压矢量相加的合成矢量U(t)就可以表示为:
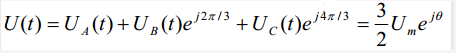
空间矢量的表示形式有三种:a∠θ=a(cosθ+jsinθ)=ae
jθ
可见U(t)是一个旋转的空间矢量,它的幅值为相电压幅值的3/2倍,Um为相电压幅值,且以角频率ω=2πf旋转。而空间矢量在三相坐标系上的投影就是对称的三相正弦量。
结论:三个空间位置差120°,时间相位还差120°的正弦量的合成空间矢量的幅值是相电压幅值的3/2倍。
2、SVPWM调制中相电压的幅值
由于逆变器三相桥臂共有6个开关管,为了研究各相上下桥臂不同开关组合时逆变器输出的空间电压矢量,特定义开关函数 Sx ( x = a、b、c) 为:

(Sa、Sb、Sc)的全部可能组合共有八个,包括6个非零矢量 Ul(001)、U2(010)、U3(011)、U4(100)、U5(101)、U6(110)、和两个零矢量 U0(000)、U7(111),下面以其中一 种开关 组合为例 析,假设Sx ( x= a、b、c)= (100), 此 时:

可得:Uan=2Ud /3、Ubn=-U d/3、Ucn=-Ud /3。从开关状态的不同组合中,不管你怎么组,搅破脑汁也只能最大到2Udc/3, 而相电压有是正弦的,所以相电压是幅值为2Udc/3的正弦量。根据上面的结论则合成矢量的幅值就是3/2*2Udc/3=Udc。
结论:三相电压合成的电压矢量幅值是Udc。
这里合成的矢量电压幅值是Udc,包不包括那6个非零矢量,显然包括的,他们是6个特殊开关状态位置而已;那么为什么好多教材或者是文章中写的非零基础矢量的幅值都是2/3Udc呢?
3、为什么教材中的非零基础矢量的幅值都是2/3Udc
这个我们从Clark变换说起,同一个旋转的空间矢量在静止的两相静止坐标系中投影的正弦量的幅值是在静止三相坐标系中的幅值的3/2倍。
可以叫做这样的变换为等矢量变换。而我们讲到的Clark变换是等幅变换。那么什么是等幅变换呢,是指alpha和beta的分量的幅值和三相分量的幅值要相等。为了两三相坐标系的幅值相等,所以变换有个2/3的系数,可以理解为缩小了1.5倍。所以合成矢量也缩小了1.5倍。所以非零基础矢量的幅值在两相静止坐标系中变为了2/3Udc。教材上说非零基础矢量的幅值是2/3Udc是因为这里说到了这个非零矢量,说到了这个傅秒原理合成等等的,已经是在两相系中看待问题了,也就是等幅值变换的alpha和beta轴中看待问题了。
结论:如果认为是Udc这是在三相系中看的结果,也是在等矢幅变换后的x-y坐标系中看的结果;如果认为是2Udc/3,这就是在等幅值变换的alpha-beta坐标系中看的结果;
4、那6个非零基础矢量的幅值到底是Udc还是2Udc/3有影响最终定时器的占空比输出嘛?
4.1、伏秒平衡原理

其中非零矢量的幅值相同(模长暂定 2Udc/3),相邻的矢量间隔 60°,而两个零矢量幅值为零,位于中心。在每一个扇区,选择相邻的两个电压矢量以及零矢量,按照伏秒平衡的原则来合成每个扇区内的任意电压矢量,即:
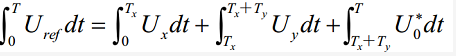
或者等效成下式:
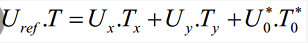
其中,Uref 为期望电压矢量;T 为采样周期;Tx、Ty、T0* 分别为对应两个非零电压矢量 Ux、Uy 和零电压矢量U 0
在一个采样周期的作时间;其中U 0
包括了 U0 和 U7 两个零矢量。式子的意义是,矢量 Uref 在 T 时间内所产生的积分效果值和 Ux、Uy、U 0
分别在时间 Tx、Ty、T0
内产生的积分效果相加总和值相同。
这里非零矢量幅值多大,其实关乎的是Uref最大能到多大,不管非零矢量U(1
6)多大,沿着正六边形走,Uref最大只能是U(1
6),沿着圆形走,不失真的情况下,最大只能到 sqrt(3)
U(1~6)/2这么大。
4.2、两个相邻的非零基础矢量合成任意矢量的作用时间
今假设欲合成的电压向量 Uref 在第Ⅰ区中第一个增量的位置,如图 2-10 所示,欲用 U4、U6、U0 及 U7 合成,用平均值等效可得:U
ref
*Tz=U
4
*T4+U
6
*T6.

在两相静止参考坐标系(α,β)中,令 Uref 和 U4 间的夹角是 θ,由正弦定理可得:
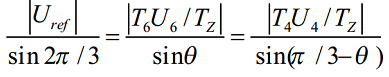
因为 U4 = 2*Udc / 3,所以可以得到各矢量的状态保持时间为
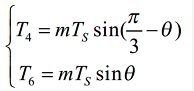
式中 m 为 SVPWM 调制系数(调制比),m=sqrt(3)|U
ref
|/Udc。而零电压向量所分配的时间为:
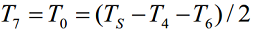
4.2的公式1是相对独立的,和U(1-6)等于多大没有关系,4.2的公式2才把U(1-6)等于多大带入到了m中,引入了Udc,它这里认为U(1~6) = 2/3Udc,所以才有了上面4.2的公式2表达式,我们这里来还原m,让他和Udc无关;
如果我们用Uo代替U(1~6)非零基础矢量,来还原m,则就是:
m = 2 * (根号3) / 3 * |Uref| / |Uo|;
这样的m就和Udc没关系了,而T4,T6又和m有关系,这里明显可以看到时间就是和Uref的大小有关系啊,Uref最大只能取到Uo或者不失真的到sqrt(3) / 2 * Uo,这么看来不管U(1~6) 等于多大,T4,T6的最大的时间是不会变的,这就是物理含义啊;
其实在4.2的式2中角度θ决定决定了两个相邻的非零基础矢量的作用时间的比值,即合成矢量的方向。m决定合成矢量的幅值。
不管你们认为U(1~6)等于多大的Udc,我定时器能给出来的占空比的变化范围是一致的;
如果认为U(1~6) 是等于2/3Udc,那我们认为Uref最大只能到2/3Udc,或者2/3Udc * (根号3) / 2;
如果认为U(1~6) 是等于Udc,那我们认为Uref最大只能到Udc,或者Udc * (根号3) / 2;
但是不管U(1~6) 等于谁,MCU对pwm操作的高低电平的时间规律是不会变的,这就是重点。
如果按照教材中的非零基础矢量的模长为2/3Udc。也可以简单的如下理解。比如非零基础矢量U1 其由三相电压 2/3Udc,-1/3Udc,-1/3Udc合成。则把他们代入到clark变换中,得到ualpha,ubeta。 由ualpha,ubeta计算模长就是等于2/3Udc。其他非零基础矢量同理。