0. 题目分析
project2要求实现一个并行决策树算法。
初步计划是实现并行化的随机森林,因为随机森林在训练时,树与树之间是相互独立的,可以很简单地实现并行化,而GBDT算法在迭代的过程中,下一棵树的生成依赖上一棵树的残差,是串行化的,没有并行化的思路。
后来发现有实现GBDT并行化的XGBoost和lightGBM,而用lightGBM训练出的成绩比自己实现的随机森林要好,于是最终使用lightGBM来完成项目
下面是完成该项目时查阅的资料和学习过程
1. CART决策树
随机森林和GBDT通常使用CART决策树作为基学习器
概念
Classification And Regression Tree,即分类回归树算法,简称CART算法,它是决策树的一种实现,通常决策树主要有三种实现,分别是ID3算法,CART算法和C4.5算法。
CART算法是一种二分递归分割技术,把当前样本划分为两个子样本,使得生成的每个非叶子结点都有两个分支,
因此CART算法生成的决策树是结构简洁的二叉树。由于CART算法构成的是一个二叉树,它在每一步的决策时只能是“是”或者“否”,即使一个feature有多个取值,也是把数据分为两部分。
在CART算法中主要分为两个步骤
- 将样本递归划分进行建树过程
- 用验证数据进行剪枝
原理
划分:
设
x
1
,
x
2
,
.
.
.
,
x
n
x_1, x_2, …, x_n
x
1
,
x
2
,
.
.
.
,
x
n
代表单个样本的
n
n
n
个特征,
y
y
y
表示样本label。CART算法通过递归的方式将
n
n
n
维的空间划分为不重叠的矩形。划分步骤大致如下
-
选一个自变量
xi
x_i
x
i
,再选取
xi
x_i
x
i
的一个值
vi
v_i
v
i
,
vi
v_i
v
i
把
nn
n
维空间划分为两部分,一部分的所有点都满足
xi
<
=
v
i
x_i<=v_i
x
i
<
=
v
i
,另一部分的所有点都满足
xi
>
v
i
x_i>v_i
x
i
>
v
i
,对非连续变量来说特征值的取值只有两个,即等于该值或不等于该值。 -
递归处理,将上面得到的两棵子树按步骤(1)重新选取一个特征继续划分,直到把整个
nn
n
维空间都划分完。
在划分时候有一个问题,它是按照什么标准来划分的 ?
对于一个特征来说,它的划分点是两个连续特征值变量的中点。
假设
m
m
m
个样本的集合一个特征有
m
m
m
个连续的值,那么则会有
m
−
1
m-1
m
−
1
个分裂点,每个分裂点为相邻两个连续值的均值。
每个特征的划分按照能减少的杂质的量来进行排序,而杂质的减少量定义为划分前的杂质减去划分后的每个节点的杂质所占比率之和。
而杂质度量方法常用
G
i
n
i
Gini
G
i
n
i
指标,假设一个样本的label共有
C
C
C
个类别,那么一个特征
A
A
A
的
G
i
n
i
Gini
G
i
n
i
不纯度可定义为
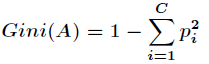
其中
p
i
p_i
p
i
表示属于第
i
i
i
个类别的概率
有了上述理论基础,实际的递归划分过程是这样的:如果当前节点的所有样本都不属于同一类或者只剩下一个样本,那么此节点为非叶子节点,所以会尝试样本的每个特征以及每个特征对应的分裂点,尝试找到杂质变量最大的一个划分,该属性划分的子树即为最优分支。
建树完成后就进行第二步了,即根据验证数据进行剪枝。在CART树的建树过程中,可能存在Overfitting,许多分支中反映的是数据中的异常,这样的决策树对分类的准确性不高,那么需要检测并减去这些不可靠的分支。决策树常用的剪枝有事前剪枝和事后剪枝,CART算法采用事后剪枝,具体方法为代价复杂性剪枝法。
下面举个简单的例子,如下图

在上述图中,特征有3个,分别是有房情况,婚姻状况和年收入,其中有房情况和婚姻状况是离散的取值,而年收入是连续的取值。拖欠贷款者属于分类的结果。
假设现在来看有房情况这个属性,那么按照它划分后的
G
i
n
i
Gini
G
i
n
i
指数计算如下
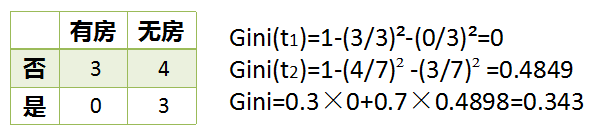
而对于婚姻状况特征来说,它的取值有3种,按照每种特征值分裂后
G
i
n
i
Gini
G
i
n
i
指标计算如下
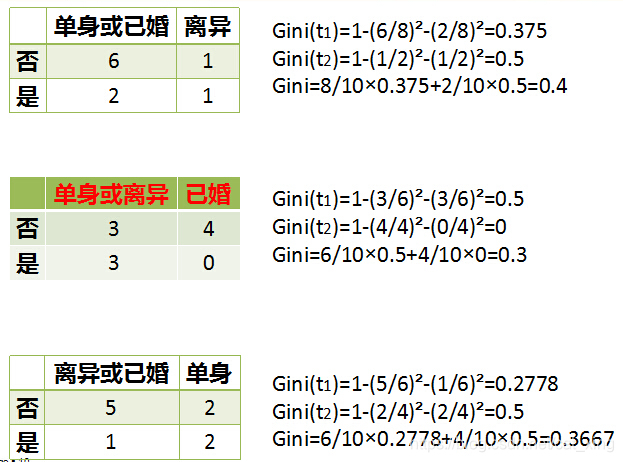
最后还有一个取值连续的特征,年收入,它的取值是连续的,那么连续的取值采用分裂点进行分裂。如下

根据这样的分裂规则CART算法就能完成建树过程。
2. 随机森林
bagging原理
bagging算法是随机森林算法的基础算法,它的特点在“随机采样”。
随机采样(bootsrap)就是从我们的训练集里面采集固定个数的样本,但是每采集一个样本后,都将样本放回。也就是说,之前采集到的样本在放回后有可能继续被采集到。
对于我们的Bagging算法,一般会随机采集和训练集样本数m一样个数的样本。这样得到的采样集和训练集样本的个数相同,但是样本内容不同。如果我们对有m个样本训练集做T次的随机采样,则由于随机性,T个采样集各不相同。
对于一个样本,它在某一次含m个样本的训练集的随机采样中,每次被采集到的概率是
1
/
m
1/m
1
/
m
。不被采集到的概率为
1
−
1
/
m
1−1/m
1
−
1
/
m
。如果m次采样都没有被采集中的概率是
(
1
−
1
/
m
)
m
(1−1/m)^m
(
1
−
1
/
m
)
m
。当
m
→
∞
m→∞
m
→
∞
时,
(
1
−
1
/
m
)
m
→
1
/
e
≃
0.368
(1−1/m)^m→1/e≃0.368
(
1
−
1
/
m
)
m
→
1
/
e
≃
0
.
3
6
8
。也就是说,在bagging的每轮随机采样中,训练集中大约有36.8%的数据没有被采样集采集中。
对于这部分大约36.8%的没有被采样到的数据,我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合,因此可以用来检测模型的泛化能力。
bagging的集合策略也比较简单,对于分类问题,通常使用简单投票法,得到最多票数的类别或者类别之一为最终的模型输出。对于回归问题,通常使用简单平均法,对T个弱学习器得到的回归结果进行算术平均得到最终的模型输出。
由于Bagging算法每次都进行采样来训练模型,因此泛化能力很强,对于降低模型的方差很有作用。当然对于训练集的拟合程度就会差一些,也就是模型的偏倚会大一些。
RF原理
随机森林(Random Forest)是Bagging算法的进化版。
首先,RF使用了CART决策树作为弱学习器。第二,在使用决策树的基础上,RF对决策树的建立做了改进,对于普通的决策树,我们会在节点上所有的
n
n
n
个样本特征中选择一个最优的特征来做决策树的左右子树划分,但是RF通过随机选择节点上的一部分样本特征,这个数字小于
n
n
n
,假设为
n
s
u
b
n_{sub}
n
s
u
b
,然后在这些随机选择的
n
s
u
b
n_{sub}
n
s
u
b
个样本特征中,选择一个最优的特征来做决策树的左右子树划分。这样进一步增强了模型的泛化能力。
如果
n
s
u
b
=
n
n_{sub}=n
n
s
u
b
=
n
,则此时RF的CART决策树和普通的CART决策树没有区别。
n
s
u
b
n_{sub}
n
s
u
b
越小,则模型越健壮,当然此时对于训练集的拟合程度会变差。也就是说
n
s
u
b
n_{sub}
n
s
u
b
越小,模型的方差会减小,但是偏倚会增大。在实际案例中,一般会通过交叉验证调参获取一个合适的
n
s
u
b
n_{sub}
n
s
u
b
的值。
除了上面两点,RF和普通的bagging算法没有什么不同, 下面简单总结下RF的算法。
输入为样本集
D
=
(
x
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
(
x
m
,
y
m
)
D={(x,y_1),(x_2,y_2),…(x_m,y_m)}
D
=
(
x
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
(
x
m
,
y
m
)
,弱分类器迭代次数
T
T
T
。
输出为最终的强分类器
f
(
x
)
f(x)
f
(
x
)
-
对于
t=
1
,
2…
,
T
t=1,2…,T
t
=
1
,
2
.
.
.
,
T
:-
对训练集进行第t次随机采样,共采集m次,得到包含m个样本的采样集
Dt
D_t
D
t
-
用采样集
Dt
D_t
D
t
训练第t个决策树模型
Gt
(
x
)
G_t(x)
G
t
(
x
)
,在训练决策树模型的节点的时候, 在节点上所有的样本特征中选择一部分样本特征, 在这些随机选择的部分样本特征中选择一个最优的特征来做决策树的左右子树划分
-
对训练集进行第t次随机采样,共采集m次,得到包含m个样本的采样集
-
如果是分类算法预测,则T个弱学习器投出最多票数的类别或者类别之一为最终类别。如果是回归算法,T个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。
并行化实现
部分代码
def learning(dataSet, times, trees):
for i in range(times):
dataTemp = bootstrap(dataSet)
trees.append(createTree(dataTemp))
if __name__ == '__main__':
trainData, testData = loadDataSet('train.csv', (0, 1000))
trees, trees1, trees2, trees3 = [], [], [], []
learning(trainData, 10, trees)
t1 = threading.Thread(target = learning, args = (trainData, 10, trees1))
t2 = threading.Thread(target = learning, args = (trainData, 10, trees2))
t3 = threading.Thread(target = learning, args = (trainData, 10, trees3))
t1.setDaemon(True); t1.start()
t2.setDaemon(True); t2.start()
t3.setDaemon(True); t3.start()
t1.join()
t2.join()
t3.join()
trees.extend(trees1)
trees.extend(trees2)
trees.extend(trees3)
classify_RF(trees, testData)
3. GBDT算法
原理
集成学习Boosting
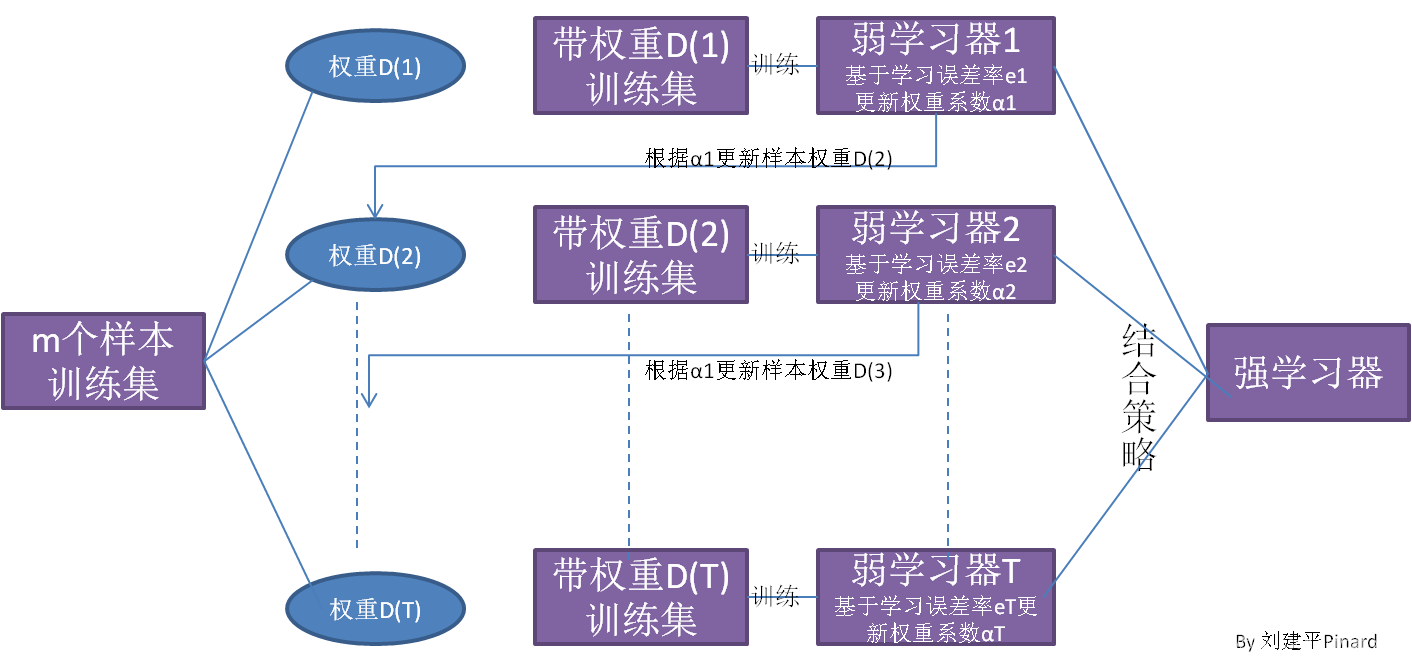
从图中可以看出,Boosting算法的工作机制是首先从训练集用初始权重训练出一个弱学习器1,根据弱学习的学习误差率表现来更新训练样本的权重,使得之前弱学习器1学习误差率高的训练样本点的权重变高,使得这些误差率高的点在后面的弱学习器2中得到更多的重视。然后基于调整权重后的训练集来训练弱学习器2,如此重复进行,直到弱学习器数达到事先指定的数目T,最终将这T个弱学习器通过集合策略进行整合,得到最终的强学习器。
GBDT是集成学习Boosting家族的成员。
在GBDT的迭代中,假设我们前一轮迭代得到的强学习器是
f
t
−
1
(
x
)
f_{t−1}(x)
f
t
−
1
(
x
)
, 损失函数是
L
(
y
,
f
t
−
1
(
x
)
)
L(y,f_{t−1}(x))
L
(
y
,
f
t
−
1
(
x
)
)
, 我们本轮迭代的目标是找到一个CART回归树模型的弱学习器
h
t
(
x
)
h_t(x)
h
t
(
x
)
,让本轮的损失函数
L
(
y
,
f
t
(
x
)
=
L
(
y
,
f
t
−
1
(
x
)
+
h
t
(
x
)
)
L(y,f_t(x)=L(y,f_{t−1}(x)+h_t(x))
L
(
y
,
f
t
(
x
)
=
L
(
y
,
f
t
−
1
(
x
)
+
h
t
(
x
)
)
最小。也就是说,本轮迭代找到决策树,要让样本的损失尽量变得更小。
GBDT的思想可以用一个通俗的例子解释,假如有个人30岁,我们首先用20岁去拟合,发现损失有10岁,这时我们用6岁去拟合剩下的损失,发现差距还有4岁,第三轮我们用3岁拟合剩下的差距,差距就只有一岁了。如果我们的迭代轮数还没有完,可以继续迭代下面,每一轮迭代,拟合的岁数误差都会减小。
大牛Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值,进而拟合一个CART回归树。第t轮的第i个样本的损失函数的负梯度表示为
r
t
i
=
−
[
∂
L
(
y
i
,
f
(
x
i
)
)
)
∂
f
(
x
i
)
]
f
(
x
)
=
f
t
−
1
    
(
x
)
r_{ti} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]_{f(x) = f_{t-1}\;\; (x)}
r
t
i
=
−
[
∂
f
(
x
i
)
∂
L
(
y
i
,
f
(
x
i
)
)
)
]
f
(
x
)
=
f
t
−
1
(
x
)
利用
(
x
i
,
r
t
i
)
(
i
=
1
,
2
,
.
.
m
)
(x_i,r_{ti})(i=1,2,..m)
(
x
i
,
r
t
i
)
(
i
=
1
,
2
,
.
.
m
)
,我们可以拟合一颗CART回归树,得到了第t颗回归树,其对应的叶节点区域
R
t
j
,
j
=
1
,
2
,
.
.
.
,
J
R_{tj},j=1,2,…,J
R
t
j
,
j
=
1
,
2
,
.
.
.
,
J
。其中J为叶子节点的个数。
针对每一个叶子节点里的样本,我们求出使损失函数最小,也就是拟合叶子节点最好的的输出值
c
t
j
c_{tj}
c
t
j
如下:
c
t
j
=
a
r
g
  
m
i
n
⎵
c
∑
x
i
∈
R
t
j
L
(
y
i
,
f
t
−
1
(
x
i
)
+
c
)
c_{tj} = \underbrace{arg\; min}_{c}\sum\limits_{x_i \in R_{tj}} L(y_i,f_{t-1}(x_i) +c)
c
t
j
=
c
a
r
g
m
i
n
x
i
∈
R
t
j
∑
L
(
y
i
,
f
t
−
1
(
x
i
)
+
c
)
这样我们就得到了本轮的决策树拟合函数如下:
h
t
(
x
)
=
∑
j
=
1
J
c
t
j
I
(
x
∈
R
t
j
)
h_t(x) = \sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj})
h
t
(
x
)
=
j
=
1
∑
J
c
t
j
I
(
x
∈
R
t
j
)
从而本轮最终得到的强学习器的表达式如下:
f
t
(
x
)
=
f
t
−
1
(
x
)
+
∑
j
=
1
J
c
t
j
I
(
x
∈
R
t
j
)
f_{t}(x) = f_{t-1}(x) + \sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj})
f
t
(
x
)
=
f
t
−
1
(
x
)
+
j
=
1
∑
J
c
t
j
I
(
x
∈
R
t
j
)
通过损失函数的负梯度来拟合,我们找到了一种通用的拟合损失误差的办法,这样无轮是分类问题还是回归问题,我们通过其损失函数的负梯度的拟合,就可以用GBDT来解决我们的分类回归问题。区别仅仅在于损失函数不同导致的负梯度不同而已。
GBDT回归算法:
输入是训练集样本
T
=
(
x
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
(
x
m
,
y
m
)
T={(x,y_1),(x_2,y_2),…(x_m,y_m)}
T
=
(
x
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
(
x
m
,
y
m
)
, 最大迭代次数T, 损失函数L。
输出是强学习器f(x)
-
初始化弱学习器
f0
(
x
)
=
a
r
g
  m
i
n
⎵
c
∑
i
=
1
m
L
(
y
i
,
c
)
f_0(x) = \underbrace{arg\; min}_{c}\sum\limits_{i=1}^{m}L(y_i, c)
f
0
(
x
)
=
c
a
r
g
m
i
n
i
=
1
∑
m
L
(
y
i
,
c
)
-
对迭代轮数t=1,2,…T有:
-
对样本i=1,2,…m,计算负梯度
rt
i
=
−
[
∂
L
(
y
i
,
f
(
x
i
)
)
)
∂
f
(
x
i
)
]
f
(
x
)
=
f
t
−
1
    
(
x
)
r_{ti} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]_{f(x) = f_{t-1}\;\; (x)}
r
t
i
=
−
[
∂
f
(
x
i
)
∂
L
(
y
i
,
f
(
x
i
)
)
)
]
f
(
x
)
=
f
t
−
1
(
x
)
-
利用
(x
i
,
r
t
i
)
(
i
=
1
,
2
,
.
.
m
)
(x_i,r_{ti})(i=1,2,..m)
(
x
i
,
r
t
i
)
(
i
=
1
,
2
,
.
.
m
)
, 拟合一颗CART回归树,得到第t颗回归树,其对应的叶子节点区域为
Rt
j
,
j
=
1
,
2
,
.
.
.
,
J
R_{tj},j=1,2,…,J
R
t
j
,
j
=
1
,
2
,
.
.
.
,
J
。其中J为回归树t的叶子节点的个数。 -
对叶子区域j =1,2,…J,计算最佳拟合值
ct
j
=
a
r
g
  m
i
n
⎵
c
∑
x
i
∈
R
t
j
L
(
y
i
,
f
t
−
1
(
x
i
)
+
c
)
c_{tj} = \underbrace{arg\; min}_{c}\sum\limits_{x_i \in R_{tj}} L(y_i,f_{t-1}(x_i) +c)
c
t
j
=
c
a
r
g
m
i
n
x
i
∈
R
t
j
∑
L
(
y
i
,
f
t
−
1
(
x
i
)
+
c
)
-
更新强学习器
ft
(
x
)
=
f
t
−
1
(
x
)
+
∑
j
=
1
J
c
t
j
I
(
x
∈
R
t
j
)
f_{t}(x) = f_{t-1}(x) + \sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj})
f
t
(
x
)
=
f
t
−
1
(
x
)
+
j
=
1
∑
J
c
t
j
I
(
x
∈
R
t
j
)
-
对样本i=1,2,…m,计算负梯度
-
得到强学习器f(x)的表达式
f(
x
)
=
f
T
(
x
)
=
f
0
(
x
)
+
∑
t
=
1
T
∑
j
=
1
J
c
t
j
I
(
x
∈
R
t
j
)
f(x) = f_T(x) =f_0(x) + \sum\limits_{t=1}^{T}\sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj})
f
(
x
)
=
f
T
(
x
)
=
f
0
(
x
)
+
t
=
1
∑
T
j
=
1
∑
J
c
t
j
I
(
x
∈
R
t
j
)
实现
class GBDT(object):
def __init__(self, n_estimators, learning_rate, min_samples_split,
min_impurity, max_depth, regression):
self.n_estimators = n_estimators
self.learning_rate = learning_rate
self.min_samples_split = min_samples_split
self.min_impurity = min_impurity
self.max_depth = max_depth
self.regression = regression
# 进度条 processbar
self.bar = progressbar.ProgressBar(widgets=bar_widgets)
self.loss = SquareLoss()
if not self.regression:
self.loss = SotfMaxLoss()
# 分类问题也使用回归树,利用残差去学习概率
self.trees = []
for i in range(self.n_estimators):
self.trees.append(RegressionTree(min_samples_split=self.min_samples_split,
min_impurity=self.min_impurity,
max_depth=self.max_depth))
def fit(self, X, y):
# 让第一棵树去拟合模型
self.trees[0].fit(X, y)
y_pred = self.trees[0].predict(X)
for i in self.bar(range(1, self.n_estimators)):
gradient = self.loss.gradient(y, y_pred)
self.trees[i].fit(X, gradient)
y_pred -= np.multiply(self.learning_rate, self.trees[i].predict(X))
def predict(self, X):
y_pred = self.trees[0].predict(X)
for i in range(1, self.n_estimators):
y_pred -= np.multiply(self.learning_rate, self.trees[i].predict(X))
if not self.regression:
# Turn into probability distribution
y_pred = np.exp(y_pred) / np.expand_dims(np.sum(np.exp(y_pred), axis=1), axis=1)
# Set label to the value that maximizes probability
y_pred = np.argmax(y_pred, axis=1)
return y_pred
优缺点
GBDT优点是适用面广,离散或连续的数据都可以处理,几乎可用于所有回归问题(线性/非线性),亦可用于二分类问题(设定阈值,大于阈值为正例,反之为负例)。缺点是由于弱分类器的串行依赖,导致难以并行训练数据。
4. lightGBM
介绍
LightGBM (Light Gradient Boosting Machine)是一个实现 GBDT 算法的框架,支持高效率的并行训练,并且具有以下优点:
- 更快的训练速度
- 更低的内存消耗
- 更好的准确率
- 分布式支持,可以快速处理海量数据
如下图,在 Higgs 数据集上 LightGBM 比 XGBoost 快将近 10 倍,内存占用率大约为 XGBoost 的1/6,并且准确率也有提升。

常用的机器学习算法,例如神经网络等算法,都可以以 mini-batch 的方式训练,训练数据的大小不会受到内存限制。
而 GBDT 在每一次迭代的时候,都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小;如果不装进内存,反复地读写训练数据又会消耗非常大的时间。尤其面对工业级海量的数据,普通的 GBDT 算法是不能满足其需求的。
LightGBM 提出的主要原因就是为了解决 GBDT 在海量数据遇到的问题,让 GBDT 可以更好更快地用于工业实践。
LightGBM 优化部分包含以下:
- 基于 Histogram 的决策树算法
- 带深度限制的 Leaf-wise 的叶子生长策略
- 直方图做差加速
- 直接支持类别特征(Categorical Feature)
- Cache 命中率优化
- 基于直方图的稀疏特征优化
- 多线程优化。
LightGBM 还具有支持高效并行的优点。LightGBM 原生支持并行学习,目前支持特征并行和数据并行的两种。
- 特征并行的主要思想是在不同机器在不同的特征集合上分别寻找最优的分割点,然后在机器间同步最优的分割点。
- 数据并行则是让不同的机器先在本地构造直方图,然后进行全局的合并,最后在合并的直方图上面寻找最优分割点。
实现
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import lightgbm as lgb
import matplotlib.pyplot as plt
x = np.array(pd.read_csv("./train/train.csv"))
y = pd.read_csv("./label/label.csv")
#划分训练集
x_train_all, x_predict, y_train_all, y_predict = train_test_split(x, y, test_size=0.10, random_state=100)
x_train, x_test, y_train, y_test = train_test_split(x_train_all, y_train_all, test_size=0.2, random_state=100)
train_data = lgb.Dataset(data=x_train,label=y_train)
test_data = lgb.Dataset(data=x_test,label=y_test)
#开始训练
param = {
'objective':'regression',
'num_leaves':119,
'max_depth':7,
'learning_rate': 0.01,
'metric': 'rmse',
}
num_round = 1000
evals_result = {}
bst = lgb.train(param, train_data, num_round, valid_sets=[test_data], early_stopping_rounds=2,evals_result=evals_result)
bst.save_model('model.txt')
bst = lgb.Booster(model_file='model.txt')
#测试集预测
ypred = bst.predict(x_predict, num_iteration=bst.best_iteration)
RMSE = np.sqrt(mean_squared_error(y_predict, ypred))
print("RMSE of predict :",RMSE)
from sklearn.metrics import r2_score
r2_score_ = r2_score(y_predict, ypred)
print('r2 score of predict :', r2_score_)
print('plt result...')
ax = lgb.plot_metric(evals_result, metric='rmse')
plt.show()
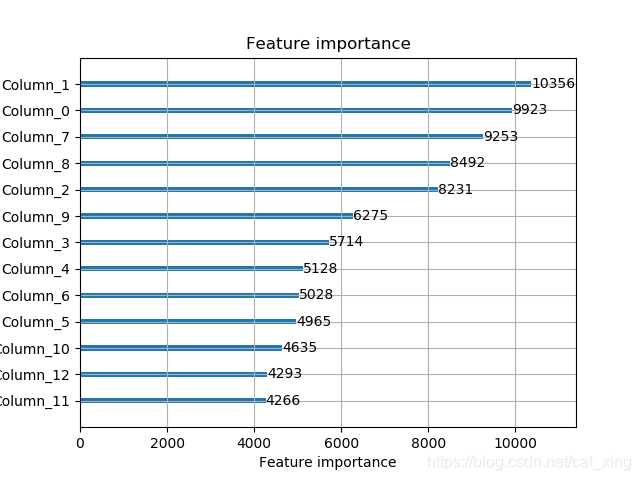
print('rank the feature...')
ax = lgb.plot_importance(bst, max_num_features=20)
plt.show()
#预测结果写入
test = pd.read_csv("./test/test.csv", header=None)
x_pred = np.array(test)
y_pred = bst.predict(x_pred, num_iteration=bst.best_iteration)
id_ = []
for i in range(len(y_pred)):
id_.append(i + 1)
dataframe = pd.DataFrame({'id':id_,'Predicted':y_pred})
dataframe.to_csv("result.csv",index=False,sep=',')
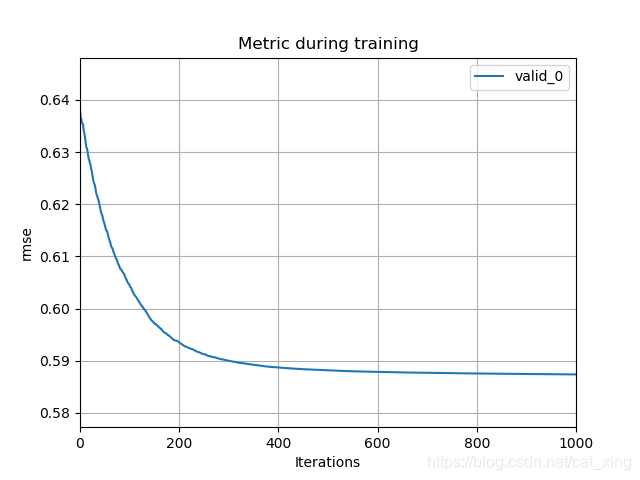
当learning rate为0.01时,rmse的变化曲线:
特征重要性排名: