一：概念

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法，归并排序对序列的元素进行逐层折半分组，然后从最小分组开始比较排序，合并成一个大的分组，逐层进行，最终所有的元素都是有序的

二：递归实现

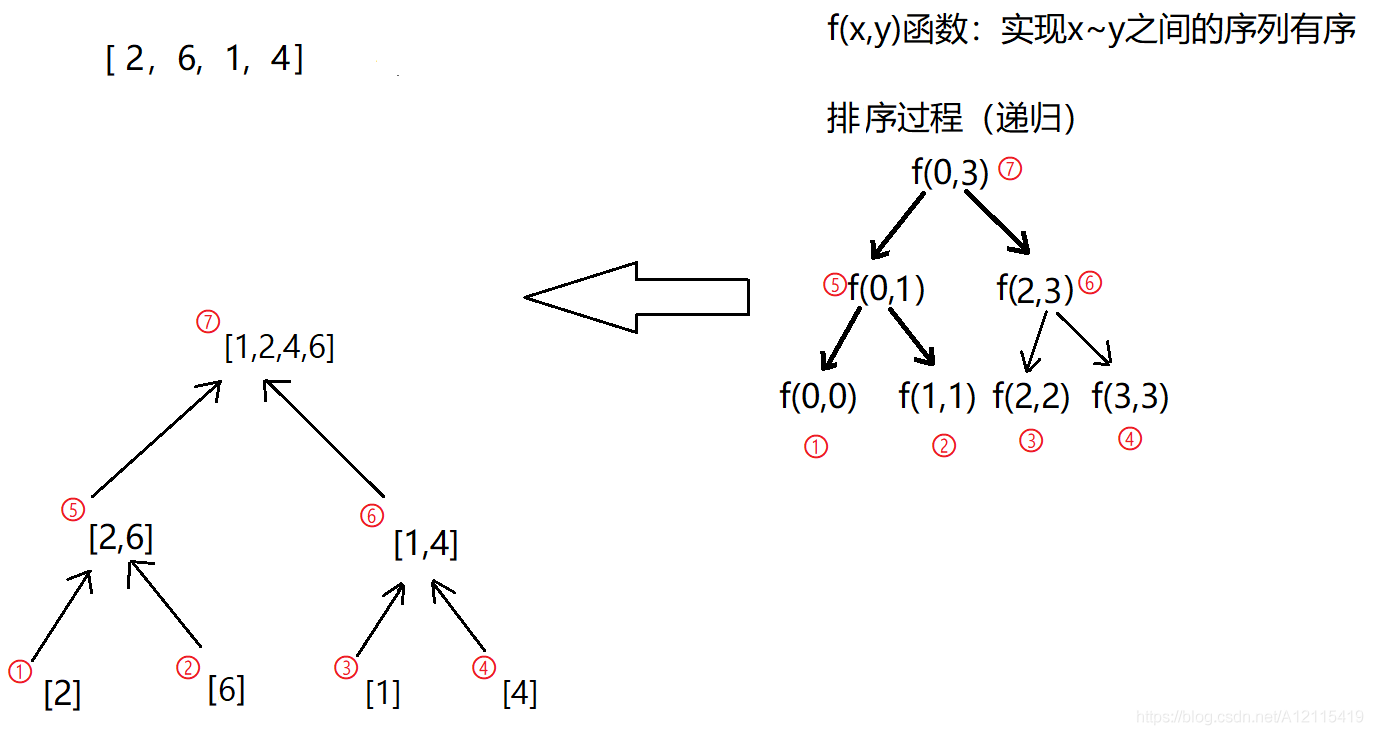
具体代码实现：


process()函数就是每次都把序列分成两部分，这样无限细分下去；

merge()函数就是精髓所在，对每一个分出的序列进行排序；

    // 递归方法实现
	public static void mergeSort1(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		process(arr, 0, arr.length - 1);
	}

    public static void process(int[] arr, int L, int R) {
		if (L == R) { 
			return;
		}
		int mid = L + ((R - L) >> 1);
		process(arr, L, mid);
		process(arr, mid + 1, R);
		merge(arr, L, mid, R);
	}

	public static void merge(int[] arr, int L, int M, int R) {
		int[] help = new int[R - L + 1];
		int i = 0;
		int p1 = L;
		int p2 = M + 1;
		while (p1 <= M && p2 <= R) {
			help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
		}
		// 要么p1越界了，要么p2越界了
		while (p1 <= M) {
			help[i++] = arr[p1++];
		}
		while (p2 <= R) {
			help[i++] = arr[p2++];
		}
		for (i = 0; i < help.length; i++) {
			arr[L + i] = help[i];
		}
	}

三：非递归实现

1.执行流程

原始序列:49 38 65 97 76 13 27

1）将原始序列看成7个只含有一个关键字的子序列，显然这些子序列都是有序的。

子序列1: 49

子序列2: 38

子序列3: 65

子序列4: 97

子序列5: 76

子序列6: 13

子序列7: 27

2）两两归并，形成若干有序二元组，即49和38归并成{38 49}，65和97归并成{65 97}，76和13归并成{13 76}，27没有归并对象，保持原样。第一趟归并排序结束，结果如下:

{38 49}，{65 97}，{13 76}，{27}

3）再将这个序列看成若干二元组子序列

子序列 1：38 49

子序列 2：65 97

子序列 3：13 76

子序列 4：27

最后一个子序列长度可能是1，也可能是2。

4）继续两两归并，形成若干有序四元组(同样，最后的子序列中不一定有4个关键字)，即{38 49}和{65 97}归并形成{38 49 65 97}，{13 76}和{27}归并形成{13 27 76}。第二趟归并排序结束,结果如下:

{38 49 65 97}，{13 27 76}

5）最后只有两个子序列了，再进行一次归并，就可完成整个归并排序，结果如下:

13 27 38 49 65 76 97

由以上分析可知，归并排序可以看作一个分而治之的过程（关于分治法，可以看本书最后一章的讲解):先将整个序列分为两半，对每一半分别进行归并排序，将得到两个有序序列，然后将这两个序列归并成一个序列即可。

具体代码实现：

    // 非递归方法实现
	public static void mergeSort2(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		int N = arr.length;
		// 步长
		int mergeSize = 1;
		while (mergeSize < N) { // log N
			// 当前左组的，第一个位置
			int L = 0;
			while (L < N) {
				if (mergeSize >= N - L) {
					break;
				}
				int M = L + mergeSize - 1;
				int R = M + Math.min(mergeSize, N - M - 1);
				merge(arr, L, M, R);
				L = R + 1;
			}
			// 防止溢出
			if (mergeSize > N / 2) {
				break;
			}
			mergeSize <<= 1;
		}
	}