博客

我们先看什么是杨辉三角：

通过观察我们得出杨辉三角的特点：

1.杨辉三角的每行第一个数字都是1。

2.杨辉三角的每行最后一个数字都是1。

3.杨辉三角从第三行开始，每行除了第一个数字和最后一个数字都是1外；

其余的数字都是每个数字的上一行同列以及上一行前一列的数字之和。

4.每行的数字个数等于这行的行数，比如第三行有3个数字，第四行有4个数字。

思路分析

1.定义一个二维数组用来存放杨辉三角的值。

#define N 6
int main(){
	int arr[N][N];//定义一个二维数组存放杨辉三角的值
    int i,j;//定义二维数组的行下角标为i,列下角标为j;

2.二维数组的每一行的第一个数字和最后一个数字都赋值为1。

for(i=0;i<N;i++){
	    arr[i][i]=1;//杨辉三角的每行最后一个数字都是1
		arr[i][0]=1;//杨辉三角的每行第一个的数字都是1
	}

3.二维数组从第三行开始，每行的第一个数字和最后一个数字都是1外，其余的数字都是每个数字的上一行同列的数字以及上一行前一列的数字之和

。

第三行数字在数组的行下角标为2。

for(i=2;i<N;i++){
		for(j=1;j<i;j++){
			arr[i][j]=arr[i-1][j]+arr[i-1][j-1];
			}    /*杨辉三角从第三行开始，每行除了第一个数字和最后一个数字都是1外，
                 其余的数字都是每个数字的上一行同列的数字以及上一行前一列的数字之和*/
	}

4.打印输出杨辉三角的前6行

 for(i=0;i<N;i++){
		for(j=0;j<=i;j++){
			printf("%d\t",arr[i][j]);
		}
		printf("\n");
	}//打印输出杨辉三角的前6行

案例全部代码如下

#include <stdio.h>
#define N 6
int main(){
	int arr[N][N];//定义一个二维数组存放杨辉三角的值
    int i,j;//定义二维数组的行下角标为i,列下角标为j;
    for(i=0;i<N;i++){
	    arr[i][i]=1;//杨辉三角的每行最后一个数字都是1
		arr[i][0]=1;//杨辉三角的每行第一个的数字都是1
	}
   for(i=2;i<N;i++){
		for(j=1;j<i;j++){
			arr[i][j]=arr[i-1][j]+arr[i-1][j-1];
			}    /*杨辉三角从第三行开始，每行除了第一个数字和最后一个数字都是1外，
                 其余的数字都是每个数字的上一行同列的数字以及上一行前一列的数字之和*/
	}
  for(i=0;i<N;i++){
		for(j=0;j<=i;j++){
			printf("%d\t",arr[i][j]);
		}
		printf("\n");
	}//打印输出杨辉三角的前6行
  return 0;
}

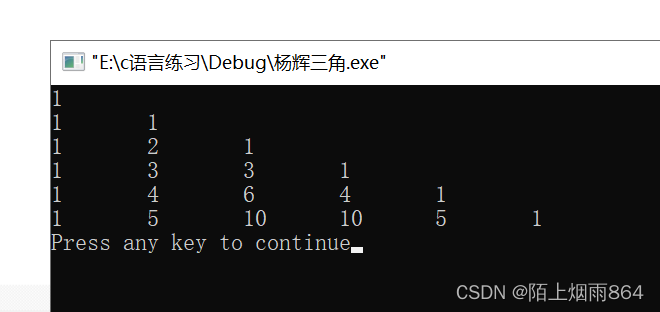
代码运行结果如下