导语
大家好,我是
智能仓储物流技术研习社
的社长,你的老朋友,
老K。
本文节选自原创电子书《
智能仓储物流技术通识与未来趋势
》,需要全版的点击此处:
原创电子书
在谈物料搬运之前,我们先来来聊聊取水的事。
在我们还没有自来水的时候,每家每户都需要到集中打水点去挑水。人每次挑两桶水倒回自家的水缸后,接着挑着
空水桶
再次返回挑水点,如此往返
循环
,直至将自家的水缸盛满。

随着现代工业技术的进步,自来水被引入到千家万户,人们无需再像以前一样一桶一桶的来回去挑,取而代之的是自来水管道直接接到了人们的家里。与挑水不同的是,自来水管道里一直都有水,人们也无需蓄水,需要水的时候,只需要拧开水龙头就可以取到水。

同样都是取水,我们可以来看看这两者的区别:
挑水:
-
人是运水的载体,每一滴水是随着人的往返循环从打水点A到家B点
-
每次人挑的水是有一定量的
-
人往回返的时候是空载
-
水缸里的水是间隔的时间才能收到水
-
可以多个人一起挑水,挑的人越多,水缸满的越早
-
不需要给人建专门的挑水的路,不占用公共资源
-
人的机动性高,打水点换了位置也没关系,人可以轻易到新的打水点取水
再看看看
自来水管:
-
水管是运水的载体,水管是不动的,每一滴水顺着水管从A点到B点
-
没有”每次”的概念,水是连续的
-
水管是一直有水流的,没有空的情况,即没有返程的概念
-
只要水龙头打开,水是没有间断的可以接收到的
-
通常只有一根主水管到B点,水的流量决定与水管的粗细
-
为了不占用人们行走的路面,水管需要建设在地下或者其他不占用公共资源的地方,需要投资
-
如果水源的位置发生了变化,水管至少有部分环节管道需要重新建设
这里将这两种取水方式简单总结一下:
-
01
机动离散式
-
02
固定连续式
而这两种取水方式也很容易连续到我们在仓储物流系统的两种搬运方式,比如从车间搬运料箱到仓库入库,同样的作业流程可以采用两种不同的方式:一种是采用叉车,多趟搬运,每次可以放多个料箱,另外一种方式是在车间和仓库之间搭建一条输送机,将料箱放到输送机上,输送机将料箱输送到仓库。
这两种不同的搬运方式在仓储物流自动化系统里,我们可以分别称之为:
离散式搬运和连续式搬运。
01-离散式搬运
离散的一个特征是可数的。对于离散式搬运我们可以很轻易的数出来当前搬运设备搬运了多少趟,每次搬运多少个物料单元,总共搬了多少个物料单元,我们也很容易数出来每小时能搬多少趟。
假如离散式搬运要完成的任务是搬运物料从A点到B点,那在B点接受物料的节奏大概如下所示:
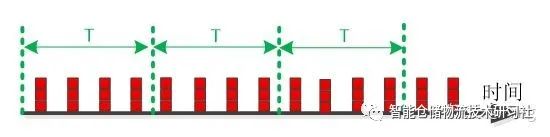
从时间轴上来看,B点接受到的物料单元是周期性的,可数的,离散式的。在图中可以很轻易的找到在单位周期时间内的搬运效率是多少。
在仓储物流自动化系统中,离散搬运系统或者设备非常多,常见的有:
叉车、AGV,穿梭车、提升机、堆垛机、机器人等。
1.离散式搬运的效率
由离散式搬运的特点,可以得知,离散式搬运系统的整体效率由如下几个方面的因素决定:
-
搬运设备的速度v
-
搬运设备的单次承载量l
-
搬运设备的数量n
离散式搬运系统的整体效率正比于v,l,n。
其中搬运设备的数量较为特殊,与v和l不同的是,v和l只关乎单个搬运设备自身的参数,而n随着数量的变化带来的效率低变化并非也直接是n倍的变化,因为设备与设备之间会互现制约的印象,设备在运行期间都会占用一定的公共资源,比如通道、收货接驳权利,送货接驳权利等等,因此n个设备的整体效率会小于n倍。设备与设备之间的制约往往会带来等待,搬运设备绕行等等的影响。
2.离散搬运效率的计算
2.1 A点到B点离散搬运效率
对于离散搬运系统的效率计算,最简单直观的方法是让搬运设备连续不停的搬运,将物料从A点搬运到B点,在B点观察并数数,可以在一定的时间T内数总共到被搬运到B点有多少个物料单元。时间T取的越长,效率评价越客观。比如在一天8个工时内,从工位A点搬运到达仓库有800个料箱,那入库的平均效率可以计算得出100个料箱/小时。
而大部分情况下,我们无法按照像上边的情形供我们去现场真的去数数,因此需要我们按照已有的条件去大概估算搬运效率。
那在我们手里,通常有哪些已知的条件呢?
搬运设备的性能特征
:
水平运行速度,垂直运行速度,单车单趟载货量,与上下游的接驳速度,多台设备之间的互相制约机制.
搬运环境参数和特征
:
运行场地的尺寸,与搬运设备有交互的交互速度
根据搬运设备的性能和搬运环境,可以得出单个搬运设备从A点到B点循环一次的周期时间T(秒),单车单趟装载量为l(个),即可以得到搬运系统的单位小时的搬运效率为(每小时可以搬运的物料单元个数):
l*3600/T(个/小时);
若有n台搬运设备同时投入运行,由于设备与设备之间有互相制约,因此综合来看每台设备的搬运效率都会打折扣,我们这里拟定折扣为k(<100%)。通常随着n的增加,k的数值往往也会增加,即设备越多,由于都占用更多的共同的公共资源,从而导致每个设备的单台效率都会降低的更多。
因此,我们可以得到有n台设备同时运行的搬运总效率为:
n*(1-k)I*3600/T(个/小时);
设备运行周期时间T定义为搬运设备从A点接驳到物料单元,再运行到B点并接驳到下游设备后,再次返回运行到A点,总共需要的时间。如果A点到B点的距离为s(设备的实际运行距离),搬运设备的平均运行速度为v,与上游接驳时间为t1,与下游接驳时间为t2,则搬运设备周期搬运时间可以得到为:
T=2s/v+t1+t2.
实际中T可能要考虑的因素要更加复杂一点:
-
搬运设备运行时可能时多个维度的机构同时动作,比如同时既有水平运行又有垂直运行,此时需要取与上下游接驳使能时之间的最大时间,比如从A点运行到B点时,设备同时需要动作水平和垂直,到B点水平位置处时,若垂直运行还未结束,则需要计算水平运行时间再加上后续额外的垂直运行时间。

-
搬运设备在运行时可能会遇到一些固定的与外部交互的时间,比如每次搬运需要在某个固定位置点等待一个工人的额外作用时间t3,此时t3也要计算到T内

-
搬运设备在运行时也可能会将运行动作转移给第三方设备,转移过程t4也要计算在内。比如搬运机器人在搬运托盘时,每次需要上电梯后并被带到更高的楼层。

-
某些搬运设备的动作比较复杂,需要逐步分解动作计算各个子动作时间,比如某些搬运设备需要转弯,转弯时的速度与垂直运行的速度并不同。

-
实际运行的设备并不是直接以平均速度运行的,有加减速的时间。

……
综合测算后的循环周期可以得到:
T=2s/v+t1+t2+t3+t4+……
根据搬运设备的性能和搬运环境,可以得出单个搬运设备从A点到B点循环一次的周期时间T(秒),单车单趟装载量为l(个),可以得到搬运系统的单位小时的搬运效率为(每小时可以搬运的物料单元个数):
E=l*3600/T(个/小时);
2.2离散的上下游的搬运效率
在仓储物流系统中,上游到下游的搬运往往不是一个简单的A点到B点,而往往是上游的A1点,A2点,A3点……,下游的是B1点,B2点,B3点……,比如从产线上生产好的成品需要入库,产品出现在产线的多个工位处A1、A2、A3,入库的时候,成品不可能只存放于仓库内的一个点,而实际情况是不同的物料会存放于不同的库位B1、B2、B3等等。
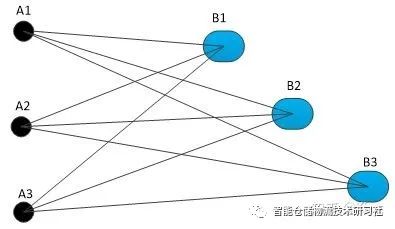
如上例中的这种离散点类的上下游搬运在实际中是更常见的,如何计算这类搬运的效率值得我们分析一下。
和计算从A点到B点的搬运效率类似,让搬运设备连续不停的从上游搬运物料到下游,我们可以在B1、B2、B3……所有的下游点观察并数数,可以在一定的时间T内数一数总共到被搬运到所有这些下游点有多少个物料单元。
从上游A1、A2……Am个上游可能接驳点到下游的B1、B2……Bn个下游的可能接驳点,其中的运行路径不止有m*n条,不同的复合行走搬运路径对应的搬运周期时间是不同的。
我们此处以2个上游点和2个下游点具体说明,从所有的上游取物料并搬运到所有的下游,如果规定从B1点出发,有如下两种搬运方案,这两种方案中的路径并不相同,因此方案1和方案2虽然都已经遍历了所有的上游和下游,但是用的时间确实大相径庭的。


事实上,如果我们开始出发点不是B1点,而是B2点,此时又会有另外两种方案3和方案4,路径也与上述的不同,自然用的时间也不同。
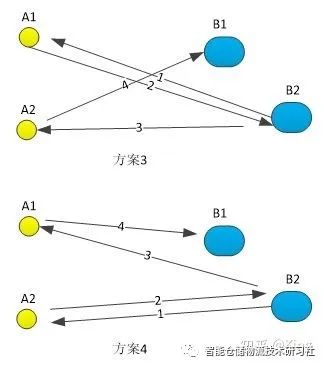
我们可以按照先按方案1从B1点出发搬运完成后回到B2点,然后按照方案3从B2点出发搬运完成后回到B1点,然后再按照方案2从B1点出发搬运完成后回到B2点,最后按照方案4从B2点出发搬运完成后回到B1。
以上通过4次不同的复合搬运作业,完成了4次不同的遍历方式,涵盖了所有的上下游的搬运方案,如果4中搬运方案出现的概率平均,并且4中方案的搬运周期分别为T1、T2、3、T4,则可以得到从上游到下游的总周期时间为:T1+T2+T3+T4。
可以得到总的平均效率为:
E=2*I*4*3600/(T1+T2+T3+T4)
;
注:
以上将2对2的所有的搬运方案当做一个循环时间来作为搬运周期,其中的搬运路径总共计算了16次(其中有若干重复),而实际中很多情况下,上游下游的数量要比2多的多,如果按照上边的计算流程来估算效率,计算的工作量非常大。
如果有m个上游点,有n个下游点,从某个下游点将每个上游点以此搬运到所有的n点,总共的搬运方案有n*m!,例如有10个上游对应10个上游的可能搬运方案有3628800个。一方面做这么大量的计算困难度大,另外一方面这么多的搬运方案作为一个整体搬运循环时间,对应到每批现实中实际搬运的作业时间也显得意义不大。
因此有必要找一种较为简单能估算出大部分搬运情况下的效率即可。
仍旧以m个上游点,n个下游点为例,如果我们从上游只选择一个点当仅有的一个上游A点,从下游只选择一个点当仅有的一个下游B点,则所有可能的AB点组合有m*n种,我们将所有组合对应的距离为d1,d2,……dmn;
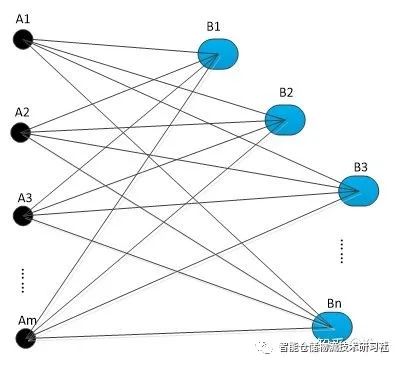
将所有的搬运距离d1~dnm进行排序可以得到如下分布:

如果我们选择最大的距离d-max对应的上下游作为AB点,则由此生成的效率会偏低,此时要满足一定的效率要求就必须要提高搬运系统的能力,比如增加设备数量,选择更高配置和性能的部件,这就意味着投资成本的增加。以最远搬运距离对应的效率为系统搬运值,会导致系统的能力过剩,因为实际的搬运作业……
后续的目录如下:


知名企业

-智能仓储物流技术研习社-
建立智能物流系统甲方、集成商与周边配套商
共同技术语言,填埋沟通鸿沟
提供高校物流专业教学现实素材
搭建可实际应用、接地气的
智能物流技术交流分享平台

立体库 | AGV | 机器人 | 拣选 | 分拣 | 仿真
| WMS | WCS | 输送 | 包装
|规划| |报告| |趋势| |历史|
制造业| 电商 | 快递 | 鞋服 | 家具 | 商超
| 零售 | 医药 | 冷链 | 第三方
往期推荐


