引入:
假设用户物品评分矩阵位R,现在有m个用户,n个物品
我们想要发现K个引雷,我们的任务就是找到两个矩阵P和Q,使这两个矩阵的乘积近似等于R,即将用户物品评分矩阵R分解称为两个低维矩阵相乘:
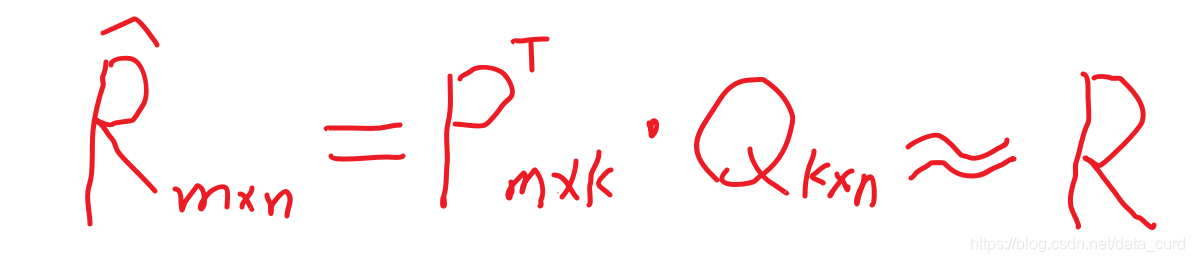
进一步理解LFM
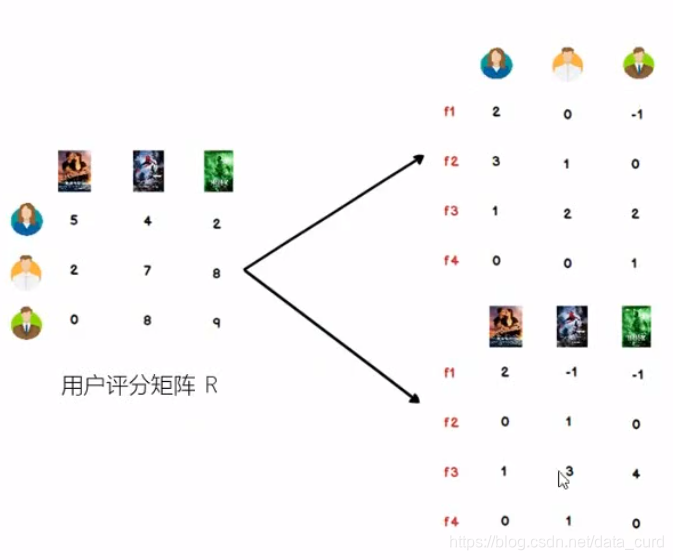
我们可以认为,用户之所以给电影打出这样的分数,是由内在原因的,我们可以挖掘出影响用户打分的隐藏因素,进而根据未评分电影与这些隐藏因素的关联度,决定此未评分电影的预测评分。
应该有一些隐藏的因素,影响用户的打分,比如电影,演员,题材,年代,,,甚至不一定是人,
直接可以理解的隐藏因子。
找到隐藏因子,可以对user和item进行关联(找到是犹豫什么使得user喜欢/不喜欢此item,什么会决定user喜欢/不喜欢item),就可以推测用户是否喜欢某一部未看过的电影。
例如:对于用户看过的电影,会有相应的打分,但一个用户不可能看过所有电影,对于用户没有看过的电影是没有评分的,因此用户评分矩阵大部分想都是空的,是一个稀疏矩阵
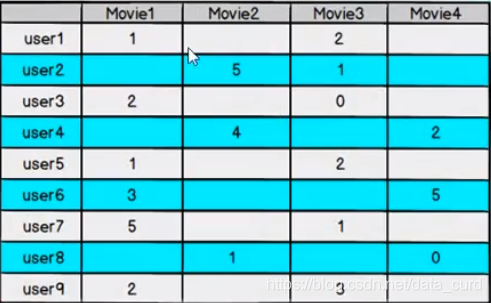
如果我们能够根据用户给已有电影的打分推测出用户会给没有看过的电影的打分,那么就可以根据预测结果给用户推荐他可能打高分的电影。
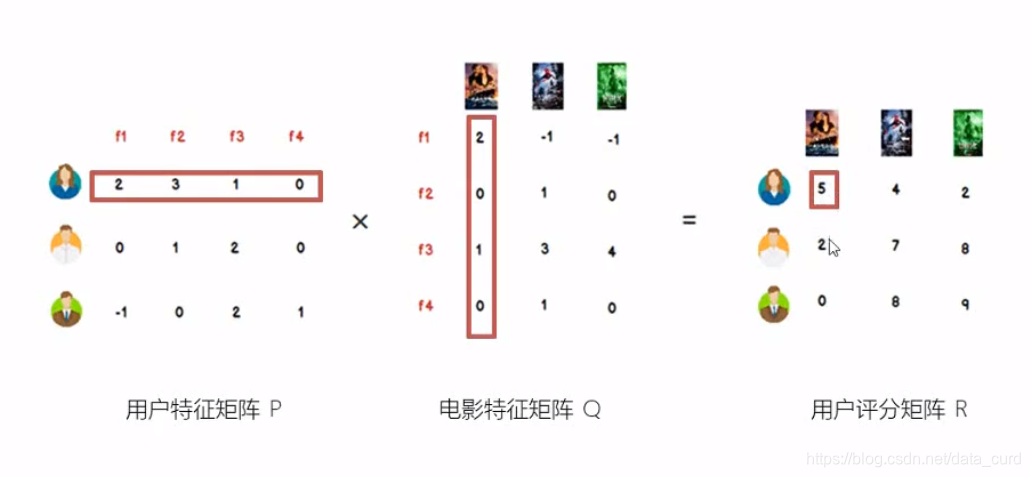
例如:一个m * n的打分矩阵R,可以用两个小矩阵P m
k 和 Q k
n 的乘积R来近似:
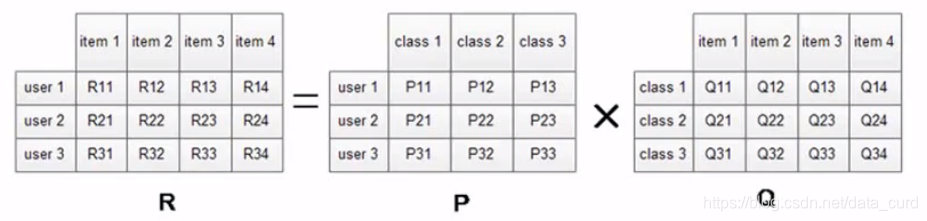
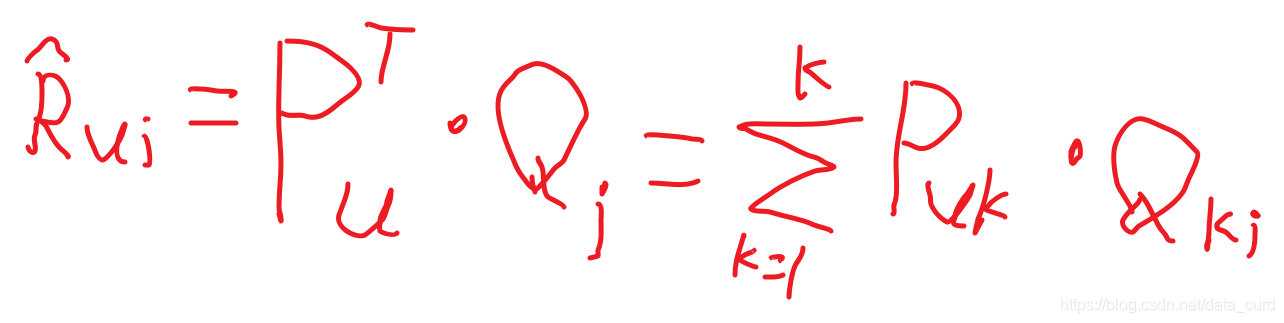
如果得到的预测评分矩阵R与原评分位置上的值都近似,那么我们认为他们的预测位置上的值也是近似的。