计算机能表示的整数范围有限,需要使用高精度计算的方法。使用一个数组 A 来表示一个大整数 a,A[0]表示 a 的个位,A[1]表示 a 的十位,依次类推。然后只需要处理数组中的每一位的数据。
大数运算
加法
代码
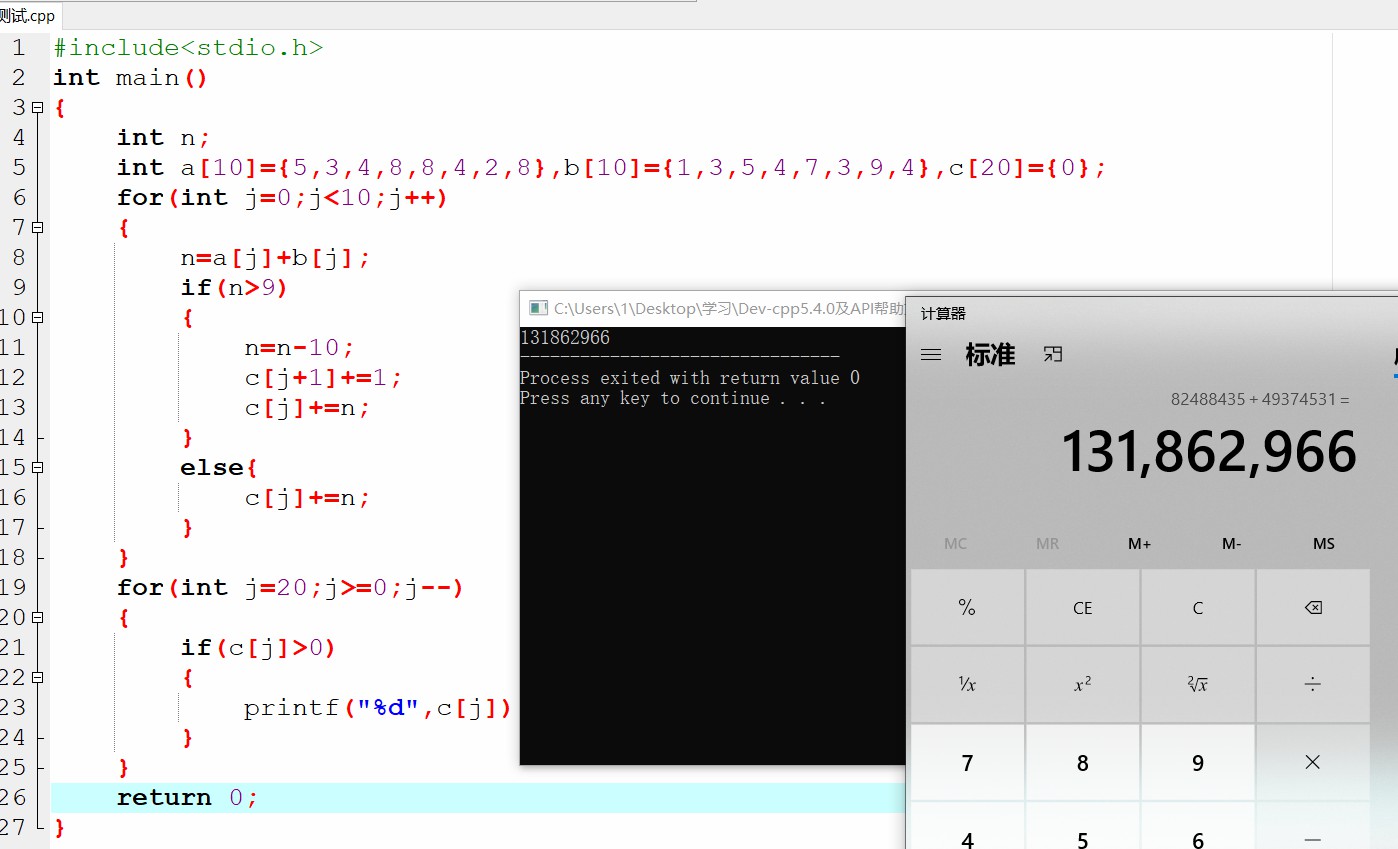
思路
遍历数组c中每一个数据,如果大于9,则需要执行进位操作
c[j]=c[j]-10;
c[j+1]=c[j+1]+1;
最后将c中储存的结果倒序输出就行了。
减法
代码
#include<stdio.h>
#include<math.h>
int dx(int aq,int bq)
{
int a;
if(aq==bq){
a=0; //减数和被减数大小相等
}
if(aq>bq){
a=1; //被减数大于减数
}
if(aq<bq){
a=2; //减数大于被减数
}
return a;
}
int main()
{
int aq=0,bq=0,ax,bx;
int a[8]={5,3,4,8,8,4,2,8},b[8]+{1,3,5,4,7,3,9,4},c[20];
for(int j=0;j<20;j++)
{
c[j]=9999;
}
for(int j=0;j<8;j++) //用加权的方法判断数组a和数组b那个大
{
if(a[j]>b[j])
{
ax=int(pow(2,j));
aq=aq+ax;
}
if(b[j]>a[j])
{
bx=int(pow(2,j));
bq=bq+bx;
}
}
if(dx(aq,bq)==0){
printf("0"); //两数相等直接输出0
}
if(dx(aq,bq)==1){
for(int j=0;j<8;j++)
{
c[j]=a[j]-b[j];
}
}
if(dx(aq,bq)==2){
for(int j=0;j<8;j++)
{
c[j]=b[j]-a[j];
}
}
for(int j=0;j<20;j++){ //遍历数组c,将其中的负数变成整数,且后一位减一,模拟“借数”
if(c[j]<0)
{
c[j]=c[j]+10;
c[j+1]=c[j+1]-1;
}
}
if(dx(aq,bq)==2){
printf("-");
}
for(int j=19;j>=0;j--)
{
if(c[j]>=0&&c[j]!=9999)
{
printf("%d",c[j]);
}
}
return 0;
}
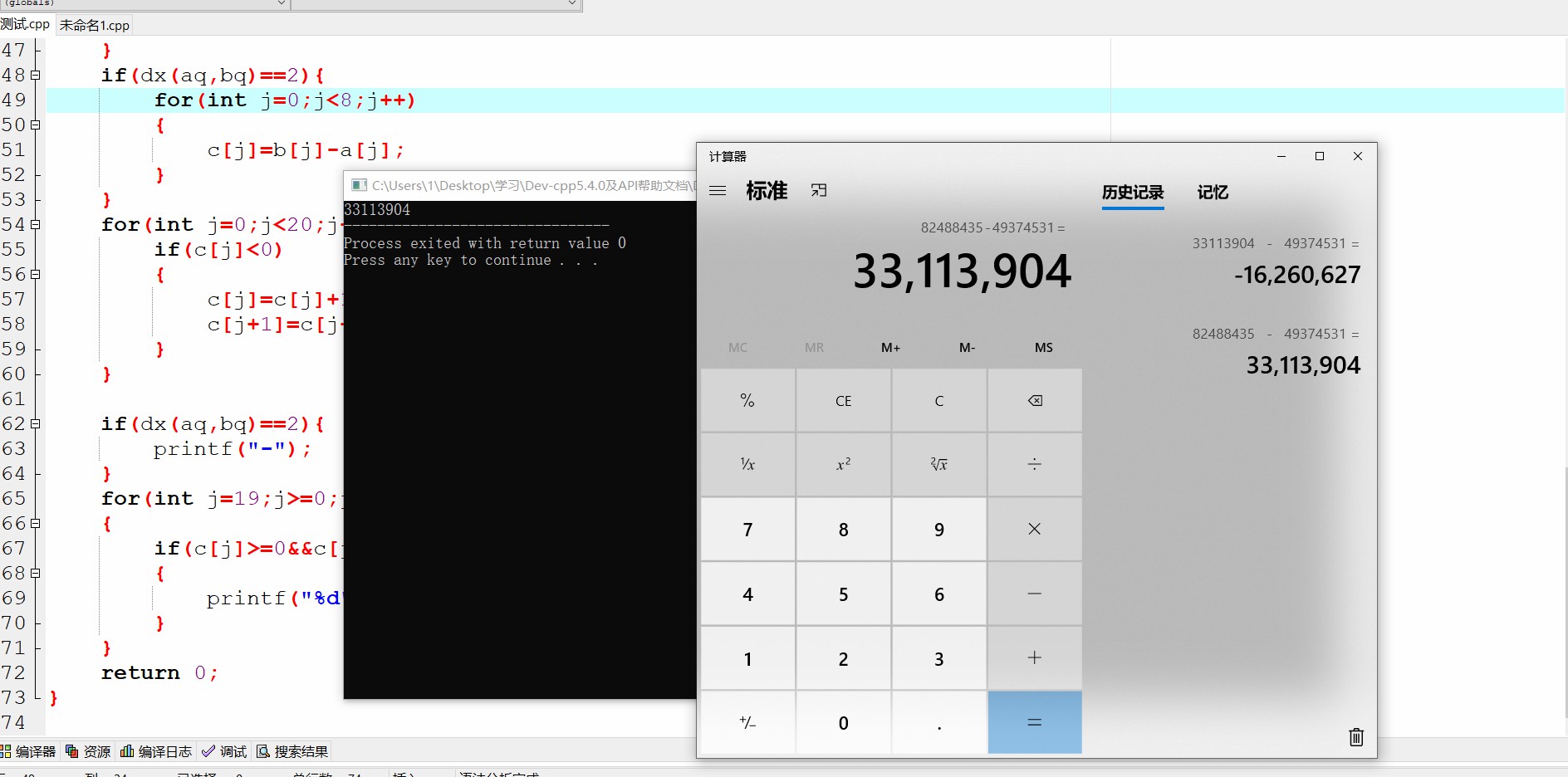
思路
在定义数组a和b时,有几个数据就定义多大的数组。
1.先用加权的方法判断a(被减数)和b(减数)里储存的数的大小,若b>a,则a与b调换位置,用b去减a,在输出最终结果是带上负号。
2.拿被减数的每一个去减对应下标的减数,并且把结果存储到对应下标的c数组中。
3.遍历检查c数组,若出现小于0的数,则模拟借位的操作。
c[j]=c[j]+10;
c[j+1]=c[j+1]-1;
4.将c中储存的结果倒序输出就行了。
乘法
代码
#include<stdio.h>
int main()
{
int a[8]={0,9,1},b[8]={0,4,5},c[7]={0},z[3][6]={0};
int n,m,r=0;
n=3; //n=乘数的位数,m=2n,数组c的大小=m+1;
m=2*n;
for(int j=0;j<n;j++) //初始化数组z
{
for(int i=0;i<m;i++)
{
z[j][i]=-2;
}
}
for(int j=1;j<n;j++) //模拟错位
{
for(int i=0;i<j;i++)
{
z[j][i]=-1;
}
}
for(int j=0;j<n;j++) //相乘
{
for(int i=0;i<n;i++)
{
for(int u=0;u<6;u++)
{
if(z[j][u]==-2){
z[j][u]=a[j]*b[i];
break;
}
}
}
}
for(int j=0;j<n;j++) //处理数组z中的数据
{
for(int i=0;i<m;i++)
{
if(z[j][i]>9)
{
if(z[j][i+1]==-2){
z[j][i+1]=z[j][i+1]+(z[j][i]/10)+2;
}
else{
z[j][i+1]=z[j][i+1]+(z[j][i]/10);
}
z[j][i]=z[j][i]%10;
}
}
}
for(int j=0;j<n;j++) //替换数组z中的-1和-2,为下一步做准备
{
for(int i=0;i<m;i++)
{
if(z[j][i]==-2||z[j][i]==-1)
{
z[j][i]=0;
}
}
}
for(int j=0;j<n;j++) //用数组c加数组z的每一行
{
for(int i=0;i<m;i++)
{
c[i]=c[i]+z[j][i];
}
}
for(int j=0;j<m+1;j++) //模拟加法进位
{
if(c[j]>9)
{
c[j+1]=c[j+1]+(c[j]/10);
c[j]=c[j]%10;
}
}
for(int j=6;j>=0;j--) //优化输出,记录结果前面的0的个数
{
if(c[j]==0)
{
r++;
}
else{
break;
}
}
for(int j=m-r;j>=0;j--) //倒序输出
{
printf("%d",c[j]);
}
return 0;
}
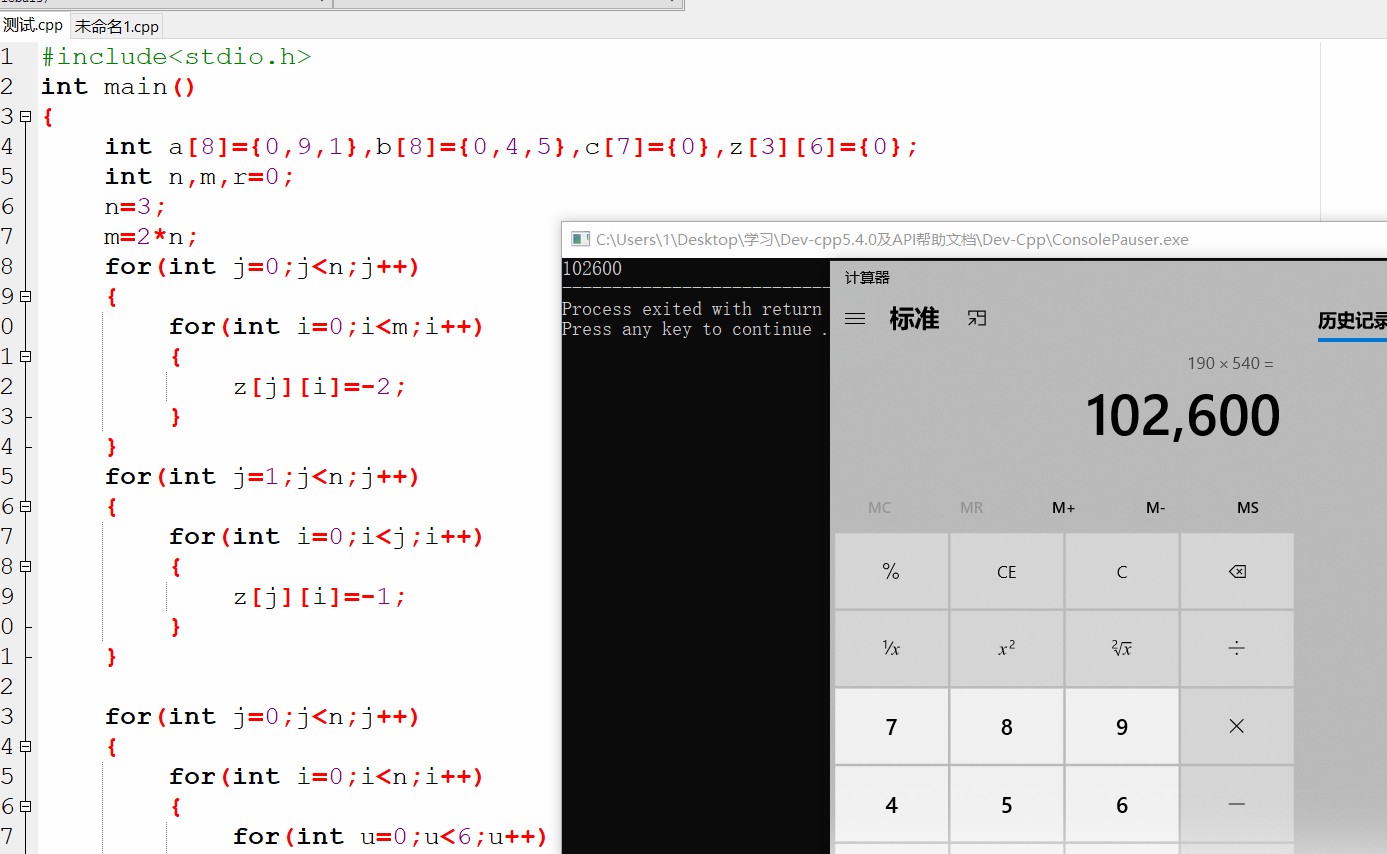
思路
1.依据乘数的位数创建数组,n等于乘数的位数,m等于2n,数组c的大小等于m+1,创建二维数组,
a[n][m],c[m+1]
。
2.因为在我们手算乘法时,每一位数乘以被乘数需要产生错位,因此我们需要进行模拟错位。就像下面把一部分-2规律的替换成-1,在进行相乘是用于区分。
| -2 | -2 | -2 | -2 | -2 |
|---|---|---|---|---|
| -1 | -2 | -2 | -2 | -2 |
| -1 | -1 | -2 | -2 | -2 |
| -1 | -1 | -1 | -2 | -2 |
3.将数组a中的每一位分别乘数组b中的每一位,将结果存在数组z中。只有数组z的位置是-2才可以存入,不然在同一行中向后判断是否可以存入。
4.整理数组z中的数据,遍历数组z的每一行,若z[j]大于9,则在同一行的后面一个数加上z[j]的十位,z[j]变为z[j]的个位。
如:12 ,3 ,6 ——> 2 ,4 ,6
5.将数组z中所有的负数替换成0,让数组c去加数组z中的每一行,再将数组c中的数据模拟进位操作。
6.倒序输出数组c。
这时会出现一个小错误,输出的结果前面会多输出几个0,用一个变量记录一下有几个0,然后优化一下输出就行了。
-2才可以存入,不然在同一行中向后判断是否可以存入。
4.整理数组z中的数据,遍历数组z的每一行,若z[j]大于9,则在同一行的后面一个数加上z[j]的十位,z[j]变为z[j]的个位。
如:12 ,3 ,6 ——> 2 ,4 ,6
5.将数组z中所有的负数替换成0,让数组c去加数组z中的每一行,再将数组c中的数据模拟进位操作。
6.倒序输出数组c。
这时会出现一个小错误,输出的结果前面会多输出几个0,用一个变量记录一下有几个0,然后优化一下输出就行了。