名称：Jacobian matrix 雅可比矩阵

用法：jacobian(f,v)

描述：jacobian(f,v) computes the Jacobian matrix of f with respect to v. The (i,j) element of the result is

jacobian(f,v) 计算了 f 关于 v 的雅可比矩阵，其第(i,j )个元素为.

输入参数说明：

f — Scalar or vector function

symbolic expression | symbolic function | symbolic vector

标量或者向量函数，符号表达式、符号函数、符号向量等。

如果f是一个标量的话，f 的雅可比矩阵是 f 的梯度的转置。

v — Vector of variables with respect to which you compute Jacobian

symbolic variable | symbolic vector

要计算雅可比的变量向量，符号变量、符号向量

如果v 是一个标量，则结果等价于 diff(f,v) 的转置。

如果v 是空符号对象，比如sym([ ])，则结果返回空符号对象。

syms x y z
f=x^3+y^3+z^3;
j=jacobian(f,[x,y,z]);
j

h=hessian(f,[x,y,z]);

h

结果为

j =
 
[ 3*x^2, 3*y^2, 3*z^2]
 
 
h =
 
[ 6*x,   0,   0]
[   0, 6*y,   0]
[   0,   0, 6*z]

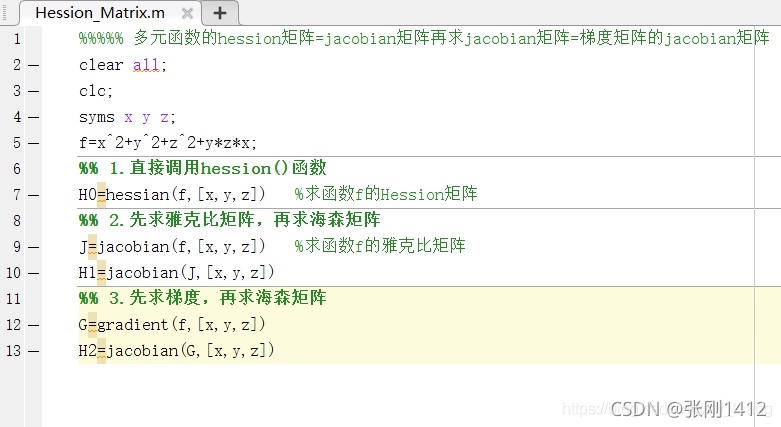
matlab求hession矩阵

MATLAB下求解多元函数的hession矩阵(3种方法)：

(1)直接调用matlab的hession函数

(2)先求雅克比矩阵，再求hession矩阵

(3)先求梯度，再求hession矩阵