前言

关于稀疏矩阵在计算机科学中的应用，
数据结构
课程可能会有所涉及，但是在各类信息学竞赛中确几乎不会出现。这是因为数据结构课程中描述的稀疏矩阵相关算法冗余难懂，使用了大量不必要的操作。而
信息学竞赛
中经常会用到

压缩空间

的技巧，这一思想可以潜移默化的转移来处理
数据结构
课程中遇到的稀疏矩阵相关的问题。本文另辟蹊径，不同于某些讲师和教材，从本质入手，提供稀疏矩阵相关的一些算法的实现。

引入

矩阵

矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合

由定义不难得知，矩阵研究的是

数

之间的关系。

在程序中表示方法

在C/C++语言中，可以使用二维数组来模拟矩阵。

局限性

但是如果当一个矩阵的行数和列数很大，例如说有一万行和一万列时候，我们需要考虑在程序中实现的可行性。

这里应该认识到，在C++默认的编译器设置中，堆区空间大小是有限的，如果我们开
int
类型的数组的话，数组的最大容量大约在

1e8

$1 e 8$

数量级，而这时这个数组已经要占用超过400MB的内存空间！

如果这个数组开在函数中例如
main
里面的话，栈区空间大小更小，只能开到

1e5

$1 e 5$

数量级。超过这个大小，程序将会出现段错误（运行错误）。

那么存储上面提到的一个巨大的矩阵的时候，我们大概需要

1e5\times1e5=1e10

$1 e 5 \times 1 e 5 = 1 e 10$

的数组容量，这需要40GB的内存空间，任何程序都是难以承受的。

但是如果这个矩阵是稀疏矩阵的话，也许我们还有方法能将它存储到程序中去。

稀疏矩阵的定义

在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵 (sparse matrix)

简单地说，如果矩阵的元素个数非常多，但其中大多数都是

0

$0$

元素（后面会知道这个多数元素只要是相等的也满足）时候，这个矩阵就被称作是一个

稀疏矩阵（sparse matrix)

。

那上面那个

1e5\times1e5

$1 e 5 \times 1 e 5$

大小的矩阵为例，虽然其中有

1e5\times1e5=1e10

$1 e 5 \times 1 e 5 = 1 e 10$

个元素，但如果其中只有几百个或者几十个元素是不为零的（与大小相差若干个数量级），那么这个矩阵就是稀疏矩阵。

稀疏矩阵的存储

这里还是遵循了
数据结构
课程上介绍的

三元组

法对稀疏矩阵进行存储

我们知道，对于每一个矩阵中的元素，我们在描述它的时候会说

第

i

$i$

行第

j

$j$

列的元素

i

j

a_{ij}

$a_{ij}$

等于XXX （

a

$a$

表示矩阵）

所以一个元素的信息包括了它所在的行数、列数以及它自身的数值

我们可以使用一个

三元组

来将这三个值存储起来，在稀疏矩阵中，我们只需要存储

非零元素

的信息

程序中存储单个元素

利用C/C++中的结构体类型来存储

我们定义一个
struct
类型

SparseMatrix

$Sp a rse M a t r i x$

里面的成员
int
型变量有行下标
row
、列下标
col
和它的值
val
（

a_{row,col}

$a_{ro w, co l}$

）

存储整个稀疏矩阵

为了表示整个稀疏矩阵，我们要将所有

非零元

的
struct

SparseMatrix

$Sp a rse M a t r i x$

存储起来。可以用数组来存，在开辟大小时候，可以预确定非零元的个数来开，这里使用
vector
来存储

有的情况下我们还需要存储原矩阵的行数和列数

创建和读取

在程序中可能要求给出的是一个以普通矩阵表示的矩阵，需要对其进行一系列操作，并将其以普通矩阵的形式输出

那么我们就需要在读入时将矩阵转化为稀疏矩阵并在输出时将稀疏矩阵的三元组形式以普通矩阵的形式进行输出

下面的操作均是在这个意义下进行的

这时候稀疏矩阵的信息应该包括原矩阵的行数和列数

读入稀疏矩阵

与普通二维数组形式的矩阵的读入类似，使用一个双重循环，分别在循环行数和列数中循环，读入一个元素，判断其是否为非零元，若为非零元，将其以及其所处的行数和列数加入到
vector
中

输出稀疏矩阵

输出问题是稀疏矩阵相关问题的难点和核心所在，有些讲师之所以设计出晦涩的代码，是因为他们没有掌握输出方面的一些要点或者技巧，以至于使用复杂的方法来实现。

思路

关键就在于

零元素

的输出

我们首先要知道零元素所处的位置，而这可以通过

相邻非零元之间的位置所确定

。与此同时，我们也知道了零元素的数量，就可以利用循环来进行输出了。

确定零元的范围

那么如何确定零元素的范围呢？

我们可以通过两个变量
lcol
和
lrow
来追踪上一个已经输出的非零元的行数和列数，然后将当前

即将

要输出的非零元的位置与它们作比较

在相应位置填补上零元并输出当前非零元后更新
lcol
和
lrow

注意

在实现过程中需要注意输出完最后一个非零元后其后面矩阵的零元也需要接着输出，这些可以通过查看下面的代码来了解

稀疏矩阵的转置

转置操作可以概括为

将矩阵元素的行和列互换

在稀疏矩阵中，我们只需要考虑非零元的变化，其余零元无论其位置变化其值是始终不变的

“转置”

“快速转置”

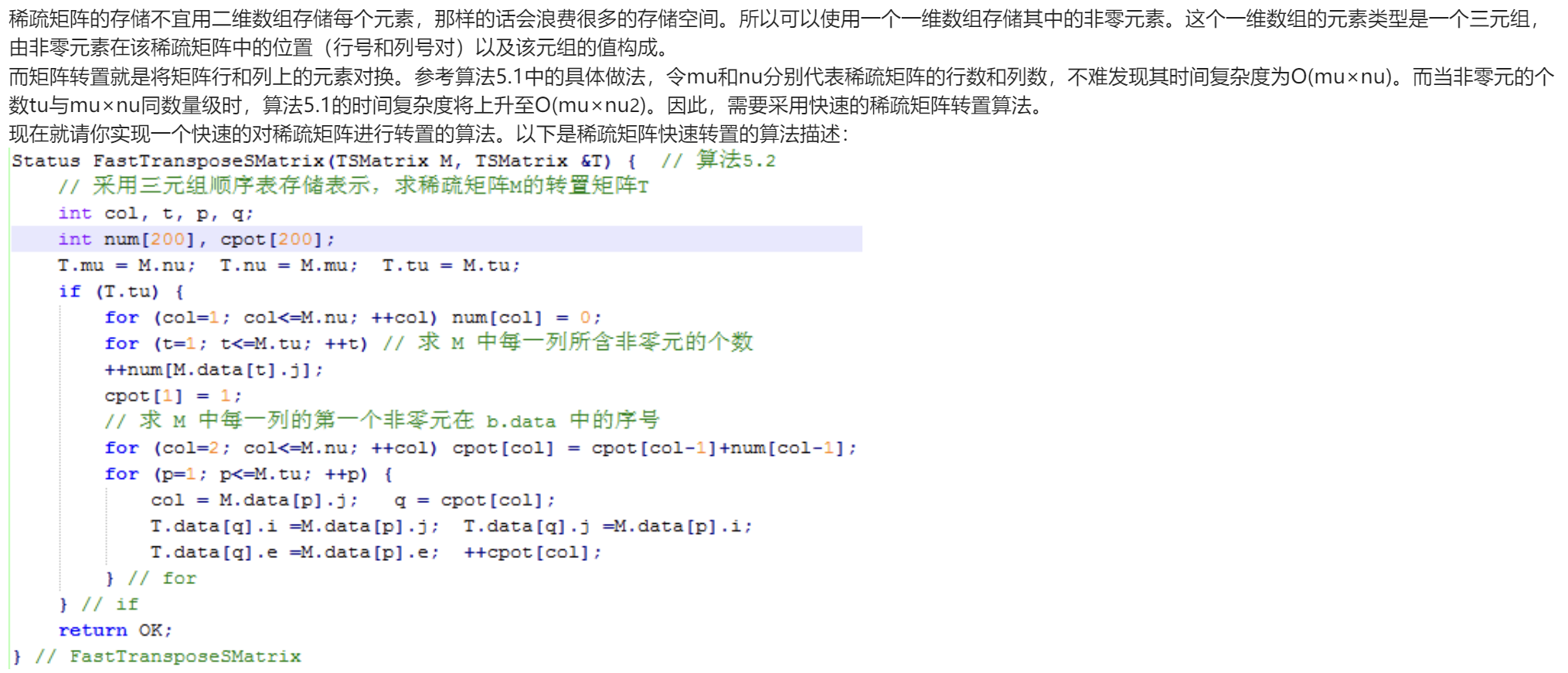
对于上面两张图表示的算法，只能表示：

emotion

实际上，将以三元组存储的稀疏矩阵转置的操作只要三步

将原矩阵的行数和列数互换
遍历三元组，对每个三元组中的行数和列数互换
将三元组重新排序

第三步需要做额外的说明，请看其存储顺序

三元组的存储顺序

回顾稀疏矩阵以普通矩阵输出的输出函数，发现我们是按

顺序

将其非零元遍历输出的。如果

顺序

是错乱的，零元的输出会出现问题。

这里的顺序指的就是在以普通矩阵的表示形式中每个元素在以行优先到列从小到大依次访问的先后次序

在读入时，它输入时的先后次序就是我们所定义的顺序，不需要额外操作

但如果在对三元组进行其他可能改变这个顺序的操作，需要对三元组进行重排

根据定义我们知道

如果行数不同，行数小的元素顺序在前
如果行数相同，列数小的元素顺序在前

于是我们可以

重载

结构体
struct

SparseMatrix

$Sp a rse M a t r i x$

中的

<

$<$

运算符

具体实现也请参照下面代码

参考代码(C++)

这个代码实现了对矩阵的转置操作

Please Forgive me those comments were writen in English

可以从中学习稀疏矩阵的存储、转置、转化和输出

/*author:Gowilli
theme:How to store and transpose a sparse matrix
*/
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
// to store non-zero elements in original matrix
// they could be descripted as the form of row-col and their own value
struct SparseMatrix
{
    int row, col, val;
    /*how to compare two sparsematrix in tuple
    evidently,this could boil down to which one would appear first
    when print the matrix manually
    so just need to compare their row and column
    */
    bool operator<(SparseMatrix const &b) const
    {
        if (row != b.row)
            return row < b.row;
        else if (row == b.row)
        {
            return col < b.col;
        }
        return true;
    }
};
/*
 the first thing that matters is how to convert a matrix to a sparse one
 and how we could output the sparse matrix into ordinary matrix form
 we could use a vector to store the tuple
 we agree that all index start from one
and all the elements in vector should be sorted in ascending order
this is automatically implemented while in reading
but you have to sort them manually when you transpose it
*/
vector<SparseMatrix> v;

// convert to sparsematrix tuple form,two parameters should be the numbers of rows and columns
void read(int n, int m)
{
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            // the elements of original matrix
            int x;
            cin >> x;
            if (x) // if read a non-zero element we need to store it to the vector
            {
                v.push_back({i, j, x});
            }
        }
    }
}
// convert  sparsematrix in tuple form to ordinary matrix,two parameters should be the numbers of rows and columns
void print(int n, int m)
{
    int lrow = 1, lcol = 0;
    for (int i = 0; i < v.size(); i++)
    {
        int row = v[i].row, col = v[i].col, val = v[i].val;
        // need fill zero between last non-zero element printed and this one
        if (lrow < row)
        {
            for (int j = lcol + 1; j <= m; j++)
                cout << 0 << " ";
            cout << endl;
            lrow++;
            while (lrow < row)
            {
                for (int j = 1; j <= m; j++)
                    cout << 0 << " ";
                cout << endl;
                lrow++;
            }
            for (int j = 1; j < col; j++)
                cout << 0 << " ";
            cout << val << " ";
        }
        else if (lrow == row)
        {
            for (int j = lcol + 1; j < col; j++)
                cout << 0 << " ";
            cout << val << " ";
        }
        else
        {
            cout << "error! check your input!" << endl;
            return;
        }
        // update recorded printed postion
        lcol = col;
    }
    // fill from last elements to the end of matrix(rightbottom)
    if (lrow < n)
    {
        for (int j = lcol + 1; j <= m; j++)
            cout << 0 << " ";
        cout << endl;
        lrow++;
        while (lrow < n)
        {
            for (int j = 1; j <= m; j++)
                cout << 0 << " ";
            cout << endl;
            lrow++;
        }
        for (int j = 1; j <= m; j++)
            cout << 0 << " ";
    }
    else if (lrow == n)
    {
        for (int j = lcol + 1; j <= m; j++)
            cout << 0 << " ";
    }
    else
    {
        cout << "error! check your input!" << endl;
        return;
    }
}

// transpose the sparsematrix,paramterer should be passed in reference form
void transpose(int &n, int &m)
{
    swap(n, m);
    for (int i = 0; i < v.size(); i++)
    {
        swap(v[i].row, v[i].col);
    }
    sort(v.begin(), v.end());
}

// main function behind is to transpose a sparse matrix
// which is input in ordinary form and require to output in ordinary form
int main()
{
    int n, m;
    cin >> n >> m;
    read(n, m);
    transpose(n, m);
    print(n, m);
    return 0;
}

（END）

ps.For students in BUCT,you could pass 算法5-1：稀疏矩阵转置 on BUCTOJ using code given above,meanwhile I would remind you this problem is suck cuz it even could pass use a two dimensional array ,so do to many other problems about sparse matrix on BUCTOJ ,those test data are too weak .

原文链接：https://blog.csdn.net/m0_61334144/article/details/127455037

前言

引入

矩阵