重点：

（1）注意去重逻辑不一样：这个事先不能排序，所以不能使用i>start&&num[i]==i-1；

——为了


记忆断开的使用情况


，如[1，2，1，1]，需要使用一个used记录使用情况；

（2）注意：需要使用所有子集，不能return，每次都需要接着来；

491. 递增子序列

难度中等508

给你一个整数数组

nums

，找出并返回所有该数组中不同的递增子序列，递增子序列中

至少有两个元素

。你可以按

任意顺序

返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

示例 1：

输入：nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

输入：nums = [4,4,3,2,1]
输出：[[4,4]]

提示：

• 
1 <= nums.length <= 15

• 
-100 <= nums[i] <= 100


解析：

也是一个子集问题，寻找出所有的子集。不过需要满足：

（1）子集的元素的数量必须大于等于2；

（2）子集中的元素必须递增；

这就导致：

（1）有重复数组，每个数字可使用一次，那么start设置为i+1；

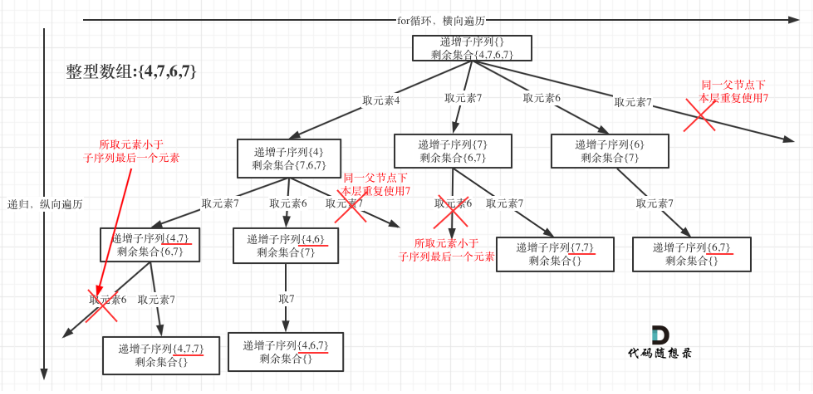
z注意这个的去重逻辑，由于顺序是断开的，


同一父节点下使用过的节点，该层不能再用，跟以前的去重逻辑不一样


。

代码：

class Solution {
private:
    vector<vector<int>> res;
    vector<int> path;
public:
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtracking(nums,0);
        return res;
    }
    void backtracking(vector<int>& nums,int start){
        int used[201]={0};
        if(path.size()>=2)
            res.push_back(path);
        for(int i=start;i<nums.size();i++){
            if(!path.empty()&&nums[i]<path.back())
                continue;
            if(i>start&&used[nums[i]+100]==1)//因为数组是断开的，used[i]==used[i-1]只能判重重复数字相邻的情况，所以需要使用used来记录1,2,1,1的情况，或者采用哈希表也可
                continue;
            path.push_back(nums[i]);
            used[nums[i]+100]=1;
            backtracking(nums,i+1);
            path.pop_back();   
        }
    }
};