二十世纪四十年代 M-P 神经元模型、Hebb 学习律出现后，五十年代出现了以感知机、Adaline 为代表的一系列成果。后来因为单层神经网络无法解决非线性问题，而多层网络的训练算法尚看不到希望，神经网络研究进入“冰河期”。哈佛大学的 Paul Werbos 在 1974 年发明 BP 算法时，正值“冰河期”，因此未受到重视。

1983 年，物理学家 John Hopfield 利用神经网络，在旅行商问题这个 NP 完全问题的求解上获得了当时最好的结果，引起轰动。稍后，UCSD 的 Rumelhart 等人重新发明了 BP 算法，再次掀起研究神经网络的热潮。二十世纪九十年代中期，随着统计学习理论和支持向量机的兴起，神经网络学习的理论性质不够清楚、试错性强、在使用中充斥大量“窍门”的弱点更为明显，于是神经网络的研究又进入低谷。

2010 年前后，随着计算能力的迅猛提升和大数据的涌现，神经网络研究在“深度学习”的名义下又重新崛起，先是在 ImageNet 等若干竞赛上以大优势夺冠，此后谷歌、百度、脸书等公司纷纷投入巨资进行研发，神经网络迎来第三次高潮。

1. 神经元模型

神经网络(neural networks)是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。

神经网络中最基本的成分是神经元(neuron)模型，即上述所说的“简单单元”。在生物神经网络中，每个神经元与其他神经元相连，当它“兴奋”时，就会向相连的神经元发送化学物质，从而改变这些神经元内的电位；如果某神经元的电位超过了一个“阈值”，那么它就会被激活，即“兴奋”起来，向其他神经元发送化学物质。

神经元

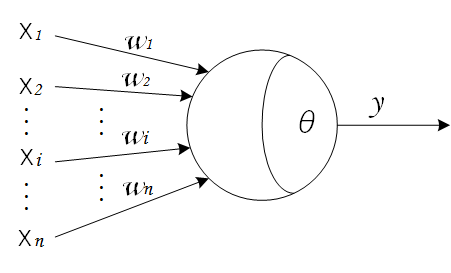
1943 年，McCulloch 和 Pitts 将上述情形抽象为上图所示的简单模型，这就是一直沿用至今的

M-P 神经元模型

。神经元接收来自

$n$
个其他神经元传递过来的输入信号

$x$
，这些输入信号通过带权重

$w$
的连接(connection)进行传递，神经元接收到的总输入值

$\sum_{i=1}^nw_ix_i$
将与神经元的阈值

$\theta$
进行比较，然后通过“激活函数”(activation function)

$f$
处理产生神经元的输出

$y=f(\sum_{i=1}^nw_ix_i-\theta)$
。

激活函数

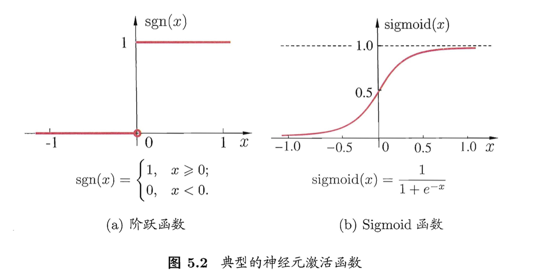
理想中的激活函数是图 5.2(a) 所示的阶跃函数，它将输入值映射为输出值

$0$
或

$1$
（

$1$
对应神经元兴奋，

$0$
对应神经元抑制）。然而，阶跃函数具有不连续、不光滑等不太好的性质，因此实际常用

$\text{Sigmoid}$
函数（即形似 S 的函数）作为激活函数。

$\text{Logistic}$
函数是典型的

$\text{Sigmoid}$
函数，它如图 5.2(b) 所示把可能在较大范围内变化的输入值挤压到

$(0,1)$
输出值范围内，因此有时也称为“挤压函数”(squashing function)。

把许多这样的神经元按一定的层次结构连接起来，就得到了神经网络。事实上，从计算机科学的角度看，我们可以先不考虑神经网络是否真的模拟了生物神经网络，只需将一个神经网络视为包含了许多参数的数学模型，这个模型是若干个函数，例如

$y_j=f(\sum_iw_ix_i-\theta_j)$
相互（嵌套）代入而得。有效的神经网络学习算法大多以数学证明为支撑。

例如 10 个神经元两两连接，则有 100 个参数：90 个连接权和 10 个阈值。

为了简化表示，通常我们把阈值

$\theta$
记为

$-w_0$
，并假想有一个附加的常量输入

$x_0=1$
，那么我们就可以把神经元的输入记为

$\sum_{i=0}^nw_ix_i$
或以向量形式写为

$\boldsymbol{w}\cdot\boldsymbol{x}$
，把输出记为

$y = f(\sum_{i=0}^nw_ix_i)$
。

2. 感知机

感知机

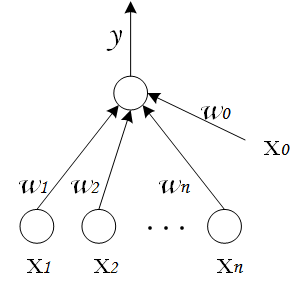
感知机由两层神经网络组成，输入层接收外界输入信号后传递给输出层，输出层是 M-P 神经元，亦称“阈值逻辑单元”(threshold logic unit)。感知机的激活函数

$f$
就是之前介绍过的阶跃函数，因而我们可以把感知机函数写为：

y = sgn (w \cdot x)

$y=\text{sgn}(\boldsymbol{w}\cdot\boldsymbol{x})$

sgn (y) = {1, if y > 0 0, otherwise

$\text{sgn}(y)=\begin{cases}1,\quad\quad \text{if}\quad y\gt0\\0,\quad\quad \text{otherwise}\end{cases}$

可以把感知机看作是

$n$
维实例空间中的超平面决策面，对于超平面一侧的实例，感知器输出

$1$
，对于另一侧的实例输出

$0$
，这个决策超平面方程是

$\boldsymbol{w}\cdot\boldsymbol{x}=0$
。那些可以被某一个超平面分割的正反样例集合称为

线性可分(linearly separable)

样例集合，它们就可以使用感知机表示。

与、或、非问题都是线性可分的问题，使用一个有两输入的感知机能容易地表示，例如：

“与”

$(x_1\wedge x_2)$
：令

$w_1=w_2=1,w_0=-2$
，则

$y=\text{sgn}(1\cdot x_1+1\cdot x_2-2)$
，仅在

$x_1=x_2=1$
时，

$y=1$
；
“或”

$(x_1\vee x_2)$
：令

$w_1=w_2=1,w_0=-0.5$
，则

$y=\text{sgn}(1\cdot x_1+1\cdot x_2-0.5)$
，当

$x_1=1$
或

$x_2=1$
时，

$y=1$
；
“非”

$(\neg x_1)$
：令

$w_1=-0.6,w_2=0,w_0=0.5$
，则

$y=\text{sgn}(-0.6\cdot x_1+0\cdot x_2+0.5)$
，当

$x_1=1$
时，

$y=0$
；当

$x_1=0$
时，

$y=1$
。

感知机训练法则

为得到可接受的权向量，我们会从随机的权值开始，反复地应用这个感知机到每个训练样例，只要它误分类样例就修改感知机的权值。重复这个过程，直到感知机正确分类所有的样例。每一步根据

感知机训练法则(perceptron training rule)

来修改权值，也就是修改与输入

$x_i$
对应的权

$w_i$
，法则如下：

w i \leftarrow w i + Δ w i

$w_i\leftarrow w_i + \Delta w_i$

Δ w i = η (t - o) x i

$\Delta w_i=\eta(t-o)x_i$

这里

$t$
是当前训练样例的目标输出，

$o$
是感知机的输出，

$\eta$
是一个正的常数称为

学习速率(learning rate)

。学习速率的作用是缓和每一步调整权的程度，它通常被设为一个小的数值（例如

$0.1$
），而且有时会使其随着权调整次数的增加而衰减。

直观来看，假定训练样本已被感知机正确分类，这时

$(t-o)=0,\Delta w_i=0$
，所以没有权值被修改。如果当目标输出是

$1$
，而感知机输出是

$0$
，为了使感知机输出正确的结果，权值必须被修改以增大

$\boldsymbol{w}\cdot\boldsymbol{x}$
的值。例如，

$x_i\gt0$
，那么增大

$w_i$
会使感知机更接近正确分类的这个示例，因为

$(t-o)$
、

$\eta$
和

$x_i$
都是正的。另一方面，如果

$t=0$
而

$o=1$
，那么和正的

$x_i$
关联的权值会被减小而不是增大。

事实上可以证明，若训练样例线性可分，并且使用了充分小的

$\eta$
，那么在有限次地使用感知机训练法则后，训练过程会收敛到一个能正确分类所有训练样例的权向量

$\boldsymbol{w}=(w_0,w_1,\cdots,w_n)$
。如果数据非线性可分，训练过程将会发生振荡(fluctuation)，

$\boldsymbol{w}$
难以稳定下来，不能求得合适解。

需要注意，感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元(functional neuron)，其学习能力非常有限。如果遇到非线性可分问题，感知机就无法表示了，例如异或这样简单的非线性可分问题。如果要解决非线性可分问题，需要使用多层功能神经元，例如使用两层的感知机就能解决异或问题：

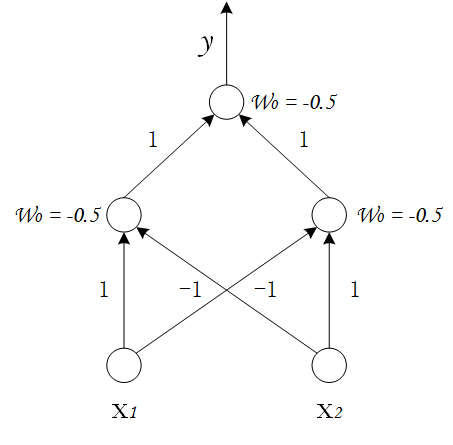
异或神经网络

上图中，输入层与输出层之间的一层神经元，被称为隐层或隐含层(hidden layer)，隐含层和输出层神经元都是拥有激活函数的功能神经元。在下一篇《神经网络（中）：多层前馈神经网络与反向传播算法》中，我们会脱离感知机探讨更为一般的多层网络结构。

参考

周志华《机器学习》

Tom M. Mitchell《机器学习》

原文链接：https://blog.csdn.net/jsksxs/article/details/72428059

1. 神经元模型

2. 感知机

感知机训练法则

参考

你可能也喜欢