1、为什么做ab
能看到这篇doc的同学 大概率其实对ab肯定有一定认知的,聊到为什么做大家多少也能聊出来诸如一下点:
小流量:
-
对于动辄日活百万、千万、甚至上亿的产品来说,小流量实验能减少试错成本;
AB随机分流
-
随机分流能很好排除confunders 的影响
统计推断科学性
-
既然是以小流量实验的结果作出对最终结果的推断,即在统计学里面是用抽样结果做对总体的推断,即必然需要考虑抽样误差,置信水平等因素(核心原理part会着重讲)
2、怎么做ab:核心原理与方法
3、怎么优化ab实验
【1】
评估结果不显著怎么办?
这个问题,绝对,绝对,绝对是避不开的!!
即使数据分析大部分时候,是要保持客观性、独立性的存在,没有PM会想自己做了很久,花了很多运营和研发的人力,但得到的是一个对业务没有正向影响的评估结果!!
因此,实验前、实验后我们都要对可能产生的不显著结果做预判准备!
还是回到影响统计推断T统计量的几个因素来看,到底是什么影响了
首先直观看公式,t统计量的值受到3个值的影响:
样本量n、样本方差、两组样本均值的差异;
三个值分别与统计显著的关系:
1、样本量越大 t检验量越大,越容易显著
2、相较于对照组的提升越大,t检验量越大,越容易显著
3、方差越小,t检验量越大,越容易显著
所以怎么提高评估敏感性呢?
-
增加样本量【流量放大实验试错成本大】
-
策略本身对评估指标有比较大的影响【没办法】
-
降低评估指标方差 【
统计科学
可以解决】

降方差方法:CUPED
1、核心思想:
CUPED(Controlled-experiment Using Pre-Experiment Data)
使用实验前的数据对实验评估指标进行修正,在保证
无偏
的情况下,得到
方差更小
从而
更敏感
的新指标,再对新指标进行统计检验。这种方法的合理性在于,实验前的数据可以解释实验评估指标的部分方差(因为二者存在一定的相关性),且与实验策略独立,因此合理地移除这部分方差不会影响实验效果的估计。
2、实现原理
控制变量法
通过选择一个已知期望且和实验评估指标强相关、与实验策略独立的控制变量来修正实验评估指标,实现方差缩减。
以回归的思想来看,实验评估指标作为y变量, 找到一个【控制变量】,不受本次策略影响,但也影响y值,来减少方差,也就是回归中【总误差和】 = 【回归平方和】+ 【残差平方和】
通常选择相同指标在实验前的数据作为控制变量,相关性大,降低方差
修正后的指标的方差 = 回归中没有被控制变量解释的那部分,也就是残差平方和 ,少掉了那部分被回归平方和解释的部分,从而实现的降低方差,从而实现更容易显著的效果。
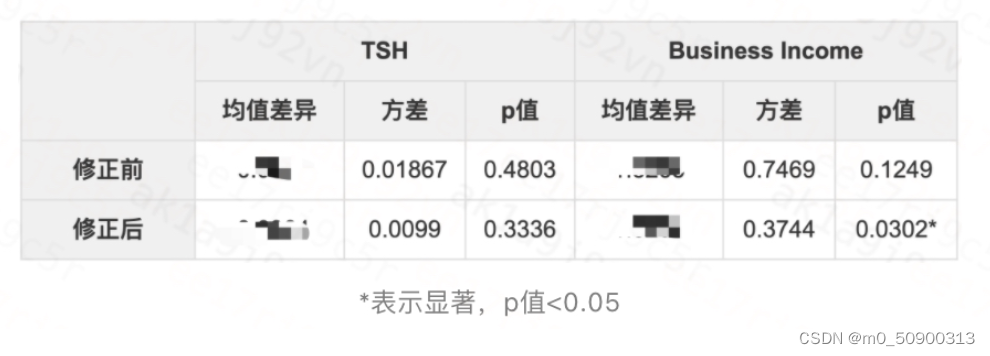
一些案例
https://exp-platform.com/Documents/2013-02-CUPED-ImprovingSensitivityOfControlledExperiments.pdf
【2】溢出效应解决
背景:
SUTVA假设 (stable unit treatment value assumption)是ABtest中比较强的一个核心假设
,即我们通常会假设实验中每个人的回应仅取决于自己的组别分配,而不取决于其他人的组别分配。
但是由于互联网业务中网络效应的天然存在,这个假设很可能难以满足。
比如测试了一种新的的推荐算法,以使其Feeds流推荐与用户更加相关来增加某些品类的购买频率。但如果用户A在策略组中下单并且与对照组中的用户B互相分享(如分享活动链接或券),则用户A的购买行为更改可能会影响用户B的购买行为。用户A可能对Feeds上的推荐品类表现出更高的购买力,因此开始共享更多的链接或活动券。最终将对用户B产生影响,用户B可能会开始购买推荐的品类而又没有新的feeds流曝光体验。这
种效应我们称之为溢出效应(spillover effect)。
导致的结果是:对照组评估指标也受到策略影响上升,从而使得策略效应被低估;
团簇分流法:引入交互关系做随机分流
为了科学的评估出策略效应,我们提出了团簇分流(cluster sampling),
也称为网络分桶(network bucketing)的解决方法,实现上其实很简单,
即随机化是在用户群集级别上进行的。换句话说,如果用户是控制组的一部分,则与他们交互连接的很大一部分也将分配给控制组。
【3】网络效应解决
背景:
上面提到的溢出效应更多是指对对照组产生了正向的影响,导致实验策略效应被低估,更多适用于比如feeds流或者在电商业务中供给无限且不价格不会动调的场景;但是我们换个业务场景,比如美团外卖和滴滴出行这种双边市场业务。
比如现在做ab,希望评估不同补贴对骑手提升工作时长、留存率、完单等指标刺激,海淀区这一块有些外卖司机5元补贴,有些8元,8元的司机努力工作了更长的时间,接了更多的单,但是该天总需求量没有变,这就导致那部分5元的司机没有单接,一下子工作意愿就下降,对照组指标虚低,实验组虚高,导致策略效应严重高估。
补充一下,这里说的高估和低估都是相对于真实放全量的理想策略效应。
时间片轮转实验:
1、
实现方式:
每天均匀分成n个时间切片,次日轮转,尽可能保证双周的实验周期,减少周期性因素的影响;
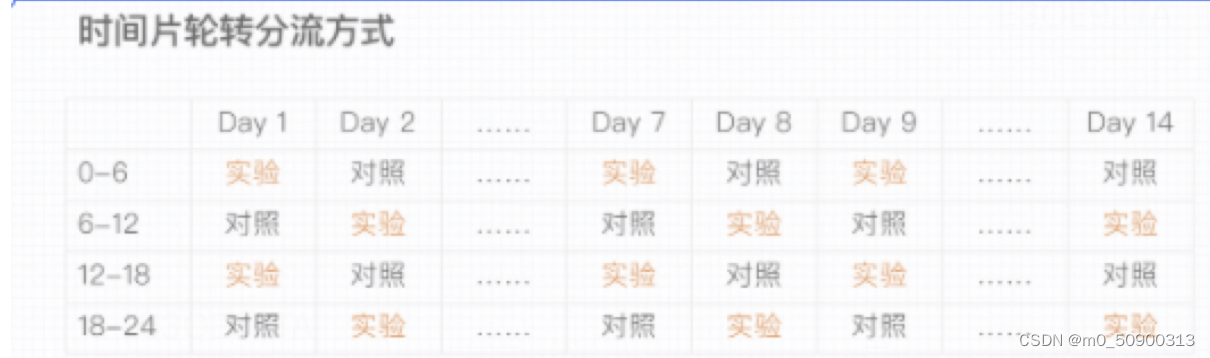
2、
适用场景:
策略效应倾向于即时生效,比如外卖和打车的补贴,用户都是大部分有即时的需求,才会去到app, 而相比之下,电商场景,很多时候,大家真的就是看看,过几天再买是常有的事情,这时候用时间片实验就不是很合适。
特别需要注意的是:这里的样本其实就是每一个时间切片,大部分场景下,14天的周期都是能够满足样本量的要求,不再有对实验城市本身用户量等计算最小样本量的约束!
3、
评估方法:
看到这里,大家肯定会有对这种实验方法的质疑,对,这个分流方式太粗了,以至于其实很难像人群粒度的随机分流一样,拉齐很多影响最终实验效果的因素,我们如果只是用t 检验进行评估,一类错误会很高,评估结果科学性欠妥。
所以我们引入了VCM的方法, VCM(Varying Coefficient Model)又称
变系数模型
,可以简单理解为对不同城市、不同时间片采用线性回归来估计策略对响应变量的影响,最后再把这些影响加和,由于加入了协变量且不同时间片系数不同,能较好控制一类错误。
相关系列更多知识:关注gzh 《大佬等我呀》