算法复习
算法填空题
子集生成
给定一个正整数集合X={x1,x2, … , xn}和一个正整数y,设计一个回溯算法求集合x的一个子集Y,使得Y中的元素之和等于y
算法如下:
输入:数组x,解向量p,开始下标from,目标y
输出:true或者false
1.若X[from]等于y,则p[from] = 1,返回ture//找到解
2.若X[from]大于y,则p[from] = 0,返回false//剪枝回溯
3.置p[from] = 1
3.1调用本算法,参数X,p,from+1,y-X[from];
3.2若算法返回true,则找到一组解,返回true
4.置p[from] = 0
4.1调用本算法,参数X,p,from+1,y
4.2若算法返回true,则找到一组解,返回true
代码:
public boolean reverse(int[] X,boolean[] p,int from,int y){
if(X[from] == y){
p[from] = true;
return true;
}
if(X[from] > y){
p[from] = false;
return fasle;
}
p[from] = true;
if(reverse(X,p,from+1,y-X[from]))
return true;
p[from] = false;
if(reverse(X,p,from+1,y))
return true;
}
全排列生成
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
算法如下:
全局变量:数组P存放符合条件的结果,对象数组result,存放结果,used Boolean[]数组,判断是否使用过
输入:数组X
输出:无
1:若数组P的长度等于X的长度,则将数组P添加到result数组中
2:循环遍历数组X[i]
2.1如果used[i]为真,则continue
2.2把used[i]置为真,并且将X[i]添加到P中
2.3再次调用本算法
2.4将X[i]从P中移除,将used置为false
class Solution {
List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
boolean[] used;
public List<List<Integer>> permute(int[] nums) {
if (nums.length == 0){
return result;
}
used = new boolean[nums.length];
permuteHelper(nums);
return result;
}
private void permuteHelper(int[] nums){
if (path.size() == nums.length){
result.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++){
if (used[i]){
continue;
}
used[i] = true;
path.add(nums[i]);
permuteHelper(nums);
path.removeLast();
used[i] = false;
}
}
}
最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
用动态规划法求两个字符串A=”xzyzzyx”
和B=”zxyyzxz”
的最长公共子序列。写出求解过程。
设的最长公共子序列的长度。动态规划函数定义为:
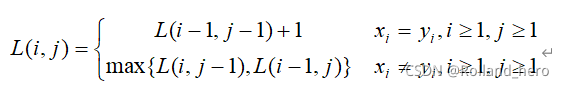
状态矩阵定义为:
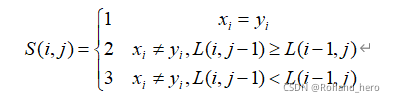
长度矩阵、状态矩阵如下:
|
B |
z | x | y | y | z | x | z | ||
|---|---|---|---|---|---|---|---|---|---|
|
A |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| x | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| z | 2 | 0 | 1 | 1 | 1 | 1 | 2 | 2 | 2 |
| y | 3 | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 2 |
| z | 4 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 3 |
| z | 5 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 |
| y | 6 | 0 | 1 | 1 | 2 | 3 | 3 | 3 | 4 |
| x | 7 | 0 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
长度矩阵L
|
B |
z | x | y | y | z | x | z | ||
|---|---|---|---|---|---|---|---|---|---|
|
A |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| x | 1 | 0 | 0 | 1 | 2 | 2 | 2 | 2 | 2 |
| z | 2 | 0 | 1 | 2 | 2 | 2 | 1 | 3 | 1 |
| y | 3 | 0 | 3 | 2 | 1 | 1 | 2 | 3 | 2 |
| z | 4 | 0 | 1 | 2 | 3 | 2 | 1 | 2 | 1 |
| z | 5 | 0 | 1 | 2 | 3 | 2 | 1 | 2 | 1 |
| y | 6 | 0 | 3 | 2 | 1 | 1 | 2 | 2 | 3 |
| x | 7 | 0 | 3 | 1 | 2 | 3 | 2 | 1 | 2 |
状态矩阵S
由长度矩阵可知,A和B的最大公共子序列长度为4。最大公共子序列为:xyyx、xyzx、zyyx、xyzz、zyzz等。
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int[][] dp = new int[text1.length() + 1][text2.length() + 1]; // 先对dp数组做初始化操作
for (int i = 1 ; i <= text1.length() ; i++) {
char char1 = text1.charAt(i - 1);
for (int j = 1; j <= text2.length(); j++) {
char char2 = text2.charAt(j - 1);
if (char1 == char2) { // 开始列出状态转移方程
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[text1.length()][text2.length()];
}
}
最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
动态规划函数定义为:
L(i)=max(L(i-1)+nums[i],nums[i])
输入:nums = [-2,1,-3,4,-1,2,1,-5,4],对应的状态如下
状态矩阵:
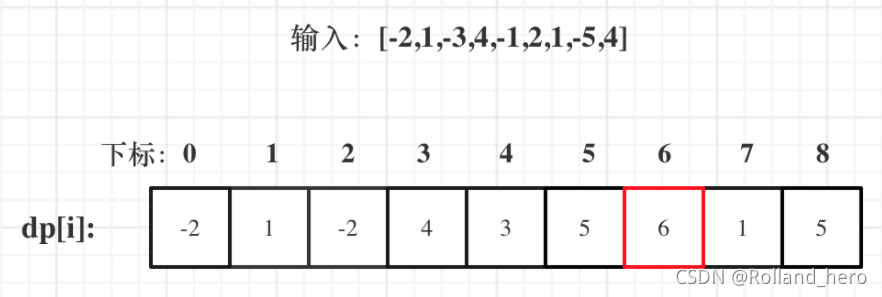
public static int maxSubArray(int[] nums) {
if (nums.length == 0) {
return 0;
}
int res = nums[0];
int[] dp = new int[nums.length];
dp[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
res = res > dp[i] ? res : dp[i];
}
return res;
}