IEEE二进制浮点数算术标准(IEEE 754)是20世纪80年代以来最广泛使用的浮点数运算标准,为许多CPU与浮点运算器所采用。这个标准定义了表示浮点数的格式(包括负零-0)与反常值(denormal number)),一些特殊数值(无穷(Inf)与非数值(NaN)),以及这些数值的“浮点数运算符”
一、名词解释
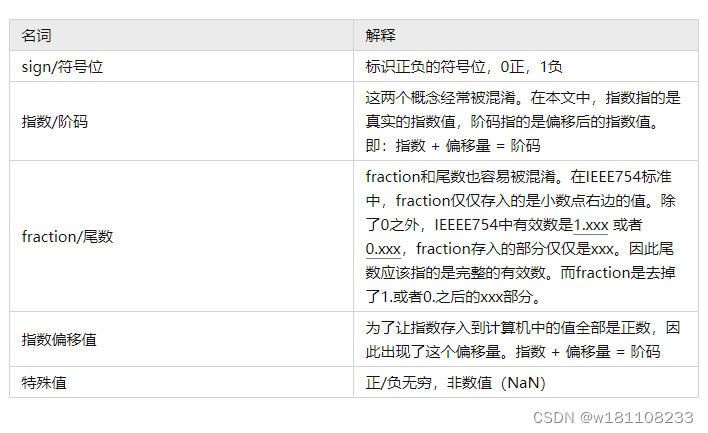
二、IEEE754标准
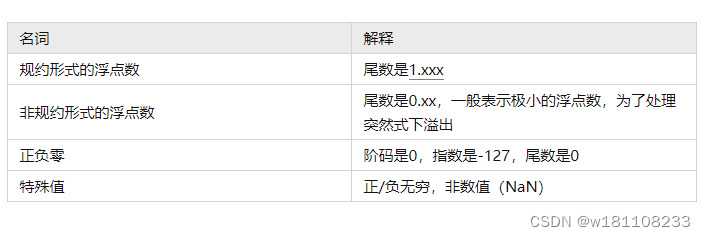
三、IEEE754标准-规约形式的浮点数
由于浮点数分为规约形式的浮点数、非规约形式的浮点数、零和特殊值。我们先不考虑非规约形式的浮点数和零和特殊值,只考虑规约形式的浮点数,下面讲的是规约形式的单精度浮点数(最常用的)。
在维基百科中,对浮点数的表示方法为:
Value(值) = sign(符号位)× exponent(阶码)×fraction(分数值/小数)
对应下面这张图片。

sign这个就是符号位,0代表正,1代表负。
01111100(二进制阶码) = 124(10进制阶码)。
算出实际的指数是124(阶码)-127(偏移量)= -3 (真实的指数)。
如果n是正,那么小数点向右移动n位,如果n为负,那么小数点向左移动n位。
图片的fraction部分省略了1,整合起来就是:1.01000000000000000000000。
根据指数n来移动小数点,因此上面算式的结果等价于:

0.00101000000000000000000000 = 0.00101。
注意!这是二进制,我们把0.00101转成10进制为:0.15625。
在PLC中的应用
IEEE754 32位浮点数格式,其结构如下

S-尾数的符号;1=负数,0 = 正数;
E-指数;与十进制数127的差值表示。
M-尾数;低23位,小数部分。
当E不全”0“时,且不全”1“时浮点数与十进制数转换公式:
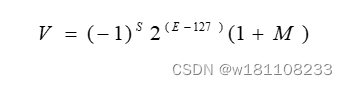
转换例程:
浮点数

S=1: 尾数符号为1表示是负数。
E = 10001000: 指数为 136
M= 001 1100 0110 0000 0000 0000,尾数为
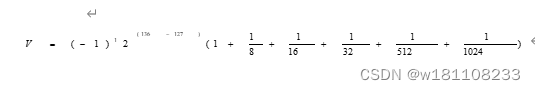
= -1 * 2^9 * 1.2216796875
= -1 * 512 * 1.2216796875
= -625.5