编译原理：正则表达式-＞NFA-＞DFA-＞DFA最小化

实验目的和要求

实验目的

正则表达式转化为DFA，主要是解决给定一个正则表达式自动转化为DFA。其目的在于了解和掌握正则表达式自动转化为DFA的过程，理解和掌握编译中的技术方法，对编译原理的教学研究有着积极的意义。通过研究可加强对学生应用能力的培养，使学生不仅具备理论知识，更要具备应用能力，使所学能为所用

实验内容

设计一个应用软件，以实现将正则表达式–>NFA—>DFA–>DFA最小化

实验要求：

（1）要提供一个正则表达式的输入界面，让用户输入正则表达式（可保存、打开保存着正则表达式的文件）

（2）需要提供窗口以便用户可以查看转换得到的NFA（用状态转换表呈现即可）

（3）需要提供窗口以便用户可以查看转换得到的DFA（用状态转换表呈现即可）

（4）需要提供窗口以便用户可以查看转换得到的最小化DFA（用状态转换表呈现即可）

支持 * + | ?（）连接

选做：画出图NFA，DFA，最小化DFA图像

实验完成情况

完成所有
必做
，实现将正则表达式–>NFA—>DFA–>DFA最小化，以状态转换表呈现，

完全按照要求进行

，指出开始节点，结束节点。
完成所有
选做
，画图支持纵向画图，横向画图，且进行

画图逻辑优化

，画出图像节点排布合理，清晰明练，线路极少交叉（默认画图会出现大量交叉边，节点排布混乱，开始结束的节点排布不合理）
测试样例完整，全面，支持用户输入测试样例，读取测试样例，随机生产测试用例，或任意点击提供的测试数据，支持
中文
，
英文
，
符号
界面设计简洁明了，任意点击
NFA转换表
，
DFA转换表
，
最小化DFA转换表
，
画NFA图
，
画DFA图
，
画最小化DFA图
，会直接读取输入框内容，无顺序要求。
对该算法的正确性做了测试。

界面如下

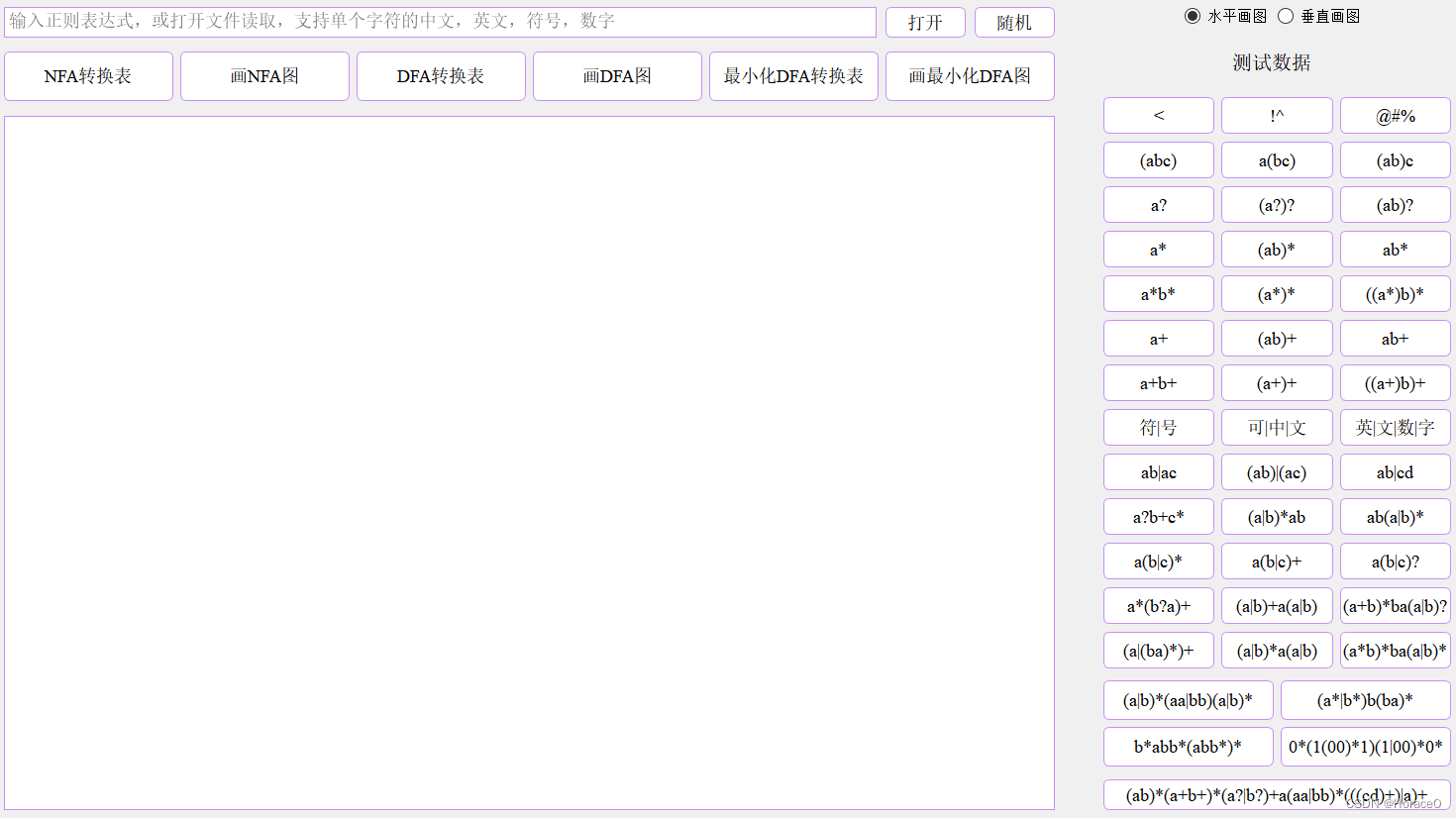
请添加图片描述

操作方法

输入框
：支持单字符中文英文符号数字，？，+，*，连接，| 运算

点击
打开
，读取测试样例

点击
随机
，随机生成测试样例

在这里插入图片描述

点击
水平画图
，图像水平伸展

在这里插入图片描述

点击
垂直画图
，图像垂直伸展

在这里插入图片描述

任意点击测试按钮，会写入输入框

在这里插入图片描述

任意点击下方按钮（无顺序要求），按钮会变紫色，即可实现对应功能
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hNG24JUk-1666978945127)(使用说明.assets/image-20221027230646131.png)]

文件说明

mian.py
——-主程序入口

nfa.py
——-nfa实验程序功能的实现

dfa.py
——-dfa实验程序功能的实现

min_dfa.py
——-min_dfa实验程序功能的实现

utils.py
——-其他程序功能的实现

draw.py
——-画图功能的实现

myui.ui
——-qt生成的ui界面文件

myui.py
——-自动转换.ui文件而生成的python代码

requirements.txt
—需要安装的依赖库（只有一个可视化库pyqt）

运行方法

安装依赖库pyqt

方案一：我们通过
pip
工具，执行命令：
pip install -r requirements.txt
，该命令会把
requirements.txt
文件中列出的库依次进行安装，最后等待安装完成即可。

方案二：
pip install pyqt5

2.安装graphviz,添加到环境变量（官网下载exe，安装时提示添加到环境变量，装了就可以画图）

运行main.py

方案一，配置pycharm点击右上角运行按钮

方案二，控制台执行
python main.py

总体方法

正则表达式：调度场算法

先添加连接符号，然后用调度场算法转为后缀表达式

原因：通用做法为进行词法分析，建立抽象语法树，但由于实验只需要接受单个字符，因此可用更简单的方法，即添加连接符号，转为后缀表达式。

正则表达式转NFA：Tompson构造法

读取后缀表达式，用Tompson构造法转NFA

原因：

优点：Tompson构造法十分直接机械，适合计算机写算法实现。

缺点：构造出的节点数非常多，转换出DFA状态数多

NFA转DFA：子集构造法

原因：子集构造法算法效率相比其他算法效率高

最小化DFA： Hopcroft 算法

原因：Hopcroft 算法效率相比其他算法效率高

测试方法：书本案例测试+多程序相互测试

1.书本案例测试：找出书本正则表达式转NFA，DFA，最小化DFA的例子，对比书本的结果

优点：答案正确

缺点：书本例子简单，且不支持？+运算符，且不够复杂

2.多程序相互测试：找班上和年级上10多位大佬的程序，编写测试样例以及随机生产测试样例，编写脚本相互验证，主要验证最小化DFA节点数，节点数是唯一的。

优点：测试样例足够复杂，足够多。

缺点：手算验证花费时间长

重要结论

：

1.大多数人的程序虽然在书本案例测试能通过，但在复杂的测试集上测试不通过，说明大多数人包括网上代码的算法设计存在问题，也帮助做错的同学纠正了自己设计的算法的错误。

2.NFA，DFA节点数可能不一样，但是最后最小化DFA节点数一定是唯一的，错误的做法得到的最小化DFA节点数通常会更少。

数据结构设计

NFA节点的类：State

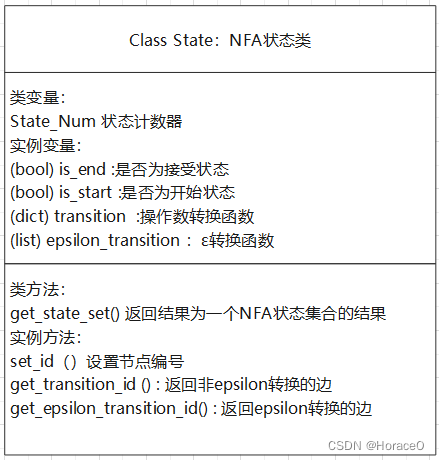
transition
字典类型，键为操作数，值为到达的NFA节点的编号

epsilon_transition
列表，经过

\epsilon

$ϵ$

转换到达的边

两个NFA节点组成一个整体

DFA节点的状态类

next
字典类型，键为操作数，值为到达的DFA节点的编号

next_group_id
字典类型，键为操作数，值为到达的DFA组节点的编号

DFA组

的状态类

NFA
，
DFA
，
DFA
组之间的逻辑关系

DFA
由多个
NFA
组成，
DFA组
由多个
DFA
组成。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yrjBcYS8-1666973145723)(实验2.assets/image-20221027113334349.png)]

算法设计

调度场算法

一般地，我们采取这样的算法转为后缀表达式

调度场算法原理：

1.遇到操作数，直接输出

2.遇到左括号，入栈

3.遇到右括号，出栈直到遇到左括号

4.遇到操作符，如果栈顶元素优先级大于等于当前操作符，出栈

5.遍历完后，将栈中剩余的操作符出栈

优先级：

prec = {
        '*': 100, '+': 100, '?': 100, '.': 80, '|': 60, ')': 40, '(': 20
    }

Thompson算法

Thompson算法：

1. 从左到右扫描正则表达式的后缀表达式

2. 遇到操作数时，构造一个NFA

3. 遇到运算符时，从栈中弹出相应数量的NFA，进行运算，将运算结果压入栈中

4. 最后栈中只有一个NFA，即为整个正则表达式对应的NFA


    stack = []
    for c in postfix:
            if c == '.':
                nfa2 = stack.pop()
                nfa1 = stack.pop()
                stack.append(from_concat(nfa1, nfa2))
            elif c == '|':
                nfa2 = stack.pop()
                nfa1 = stack.pop()
                stack.append(from_or(nfa1, nfa2))
            elif c == '*':
                nfa = stack.pop()
                stack.append(from_closure(nfa))
            elif c == '+':
                nfa = stack.pop()
                stack.append(from_closure1(nfa))
            elif c == '?':
                nfa = stack.pop()
                stack.append(from_closure0(nfa))
            else:
                stack.append(from_char(c))
    return stack.pop()

其中：

给状态添加字符转换

def add_transition(come: State, to: State, c: str):
    come.transition[c] = to

给状态添加ε转换

def add_epsilon_transition(come: State, to: State):
    come.epsilon_transition.append(to)

接收到字符，建立转换

创建开始节点，终止节点，添加转换边，如图所示

def from_char(c: str):
    start = State(is_start=True,is_end=False)
    end = State(is_start=False,is_end=True)
    add_transition(start, end, c)
    return NFA(start, end)

接收到 . 号的Thompson算法

传入两个NFA，第一个NFA的结束节点和第二个NFA节点的开始之间添加转换ε边，修改开始和结束标记，返回新NFA，以第一个为开始，最后一个为结束，如图所示

def from_concat(nfa1: NFA, nfa2: NFA):
    add_epsilon_transition(nfa1.end, nfa2.start)
    nfa1.end.is_end = False
    nfa1.start.is_start = True
    nfa2.start.is_start = False
    return NFA(nfa1.start, nfa2.end)

接收到 | 号的Thompson算法

传入两个NFA，创建一个开始节点和结束节点，按如图所示的方法添加ε边，修改开始和结束标记，返回新NFA，以第一个为开始，最后一个为结束，如图所示

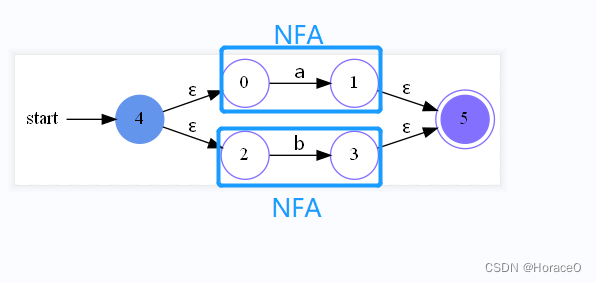
def from_or(nfa1: NFA, nfa2: NFA):
    start = State(False)
    end = State(True)
    add_epsilon_transition(start, nfa1.start)
    add_epsilon_transition(start, nfa2.start)
    add_epsilon_transition(nfa1.end, end)
    add_epsilon_transition(nfa2.end, end)
    nfa1.end.is_end = False
    nfa2.end.is_end = False
    nfa1.start.is_start = False
    nfa2.start.is_start = False
    start.is_start = True
    return NFA(start, end)

接收到* 号闭包的Thompson算法

传入1个NFA，创建一个开始节点和结束节点，按如图所示的方法添加ε边，修改开始和结束标记，返回新NFA，以第一个为开始，最后一个为结束，如图所示

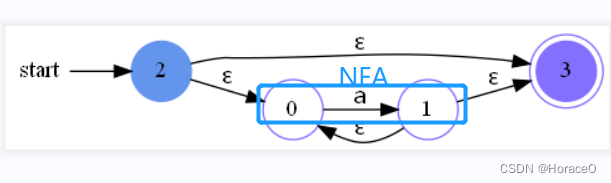
def from_closure(nfa: NFA):
    start = State(False)
    end = State(True)
    add_epsilon_transition(start, nfa.start)
    add_epsilon_transition(nfa.end, end)
    add_epsilon_transition(nfa.end, nfa.start)
    add_epsilon_transition(start, end)
    nfa.end.is_end = False
    nfa.start.is_start = False
    start.is_start = True
    return NFA(start, end)

接收到+ 号闭包的Thompson算法

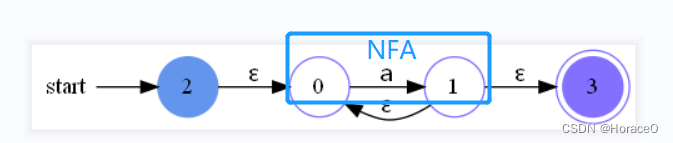
def from_closure1(nfa: NFA):
    start = State(False)
    end = State(True)
    add_epsilon_transition(start, nfa.start)
    add_epsilon_transition(nfa.end, end)
    add_epsilon_transition(nfa.end, nfa.start)
    nfa.end.is_end = False
    start.is_start = True
    nfa.start.is_start = False
    return NFA(start, end)

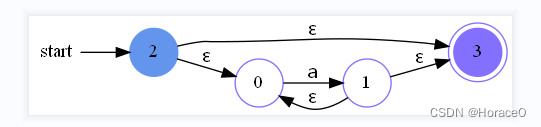
接收到? 号闭包的Thompson算法

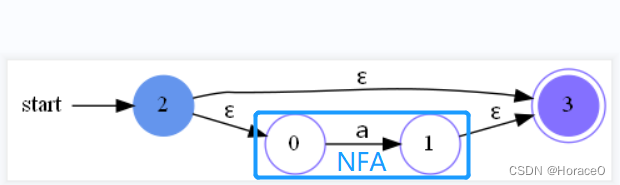
def from_closure0(nfa: NFA):
    start = State(False)
    end = State(True)
    add_epsilon_transition(start, nfa.start)
    add_epsilon_transition(nfa.end, end)
    add_epsilon_transition(start, end)
    nfa.end.is_end = False
    start.is_start = True
    nfa.start.is_start = False
    return NFA(start, end)

最后我们可以把所有节点信息整合一下，把核心信息用列表存起来，列表下标对应NFA节点的编号。主要方便画图与画表。

NFA转DFA：子集构造法

给定任意NFA，构造等效DFA（即，接受完全相同字符串的DFA）需要：

消除ε-跃迁

ε-闭包：一个或多个状态的ε-变换所能达到的所有状态的集合。

在单个输入字符上从一个状态进行多次转换。

跟踪通过匹配单个字符可以访问的状态集。

这两个过程都引导我们考虑一组状态而不是单个状态。因此，我们构造的DFA将原始NFA的状态集作为其状态集

操作	说明
ε-closrue(s)	仅在ε-转换上从NFA状态s可到达的NFA状态集
Move(A,a)	输入符号a从A中的某些NFA状态转换到的NFA状态集合。

$\epsilon ϵ 闭包$

−

(

)

∈

闭

包

\epsilon- closure (\mathrm{s}), \mathrm{s} \in \mathrm{S}_{\mathrm{NF} A} 闭包\\

$ϵ - c l o s u r e (s), s \in S_{N F A} 闭包$

输入: 一个状态集 S

输出: 所有 s 中的状态可经由任意长度的ε边能抵达的状态集合

补充：这边的状态指的是 NFA 中的状态

求ε闭包(ε转换表, 闭包):
    将闭包中的结点全部入栈
    while 栈不为空:
        结点 = 栈.pop()    
        for i in ε转换表[结点]:
            if i不在闭包中:
                将i加入闭包
                将i入栈
    return 闭包

到达闭包

⁡

(

)

∈

∑

\operatorname{move}(\mathrm{A}, \mathrm{a}), \mathrm{A} \in \mathrm{S}_{\mathrm{DFA}}, \mathrm{a} \in \sum\\

$m o v e (A, a), A \in S_{D F A}, a \in \sum$

输入: 一个 DFA 状态(即一个 NFA 的状态的集合，后续)，一个输入字符(a)

输出: DFA 状态中每个 NFA 状态透过 a 边能抵达的所有 NFA 状态的集合

求到达闭包(闭包，字符，字符转换表):
    新闭包 = []
    for 结点 in 闭包:
        if 结点可以通过字符到达:
            新闭包.append(到达结点)
    return 新闭包

nfa转dfa

nfa转dfa():
    闭包栈 = [] //待处理的DFA
    dfa状态列表 = [] //已标记的DFA
    dfa状态列表.append(DFA(开始状态的ε闭包))
    闭包栈.append(DFA(开始状态的ε闭包))        
    while 闭包栈不为空:
        dfa状态 = 闭包栈.pop()
        for 字符 in 字符表:
            新闭包 = 求到达闭包(闭包，字符，字符转换表)
            新闭包 = 求ε闭包(ε转换表, 新闭包)
            if 新闭包不为空并且新闭包不在dfa状态列表中:
                dfa状态列表.append(DFA(新闭包))
                闭包栈.append(DFA(新闭包))
                dfa状态.转换表[字符] = 新闭包的id
            else: 
                dfa状态.转换表[字符] = 新闭包的id
    return dfa状态列表

def nfa2dfa(id: list, char_transition: list, epsilon_transition: list, is_end: list, is_start: list, alnum_set: set):

    closure_list = []  # 闭包栈
    dfa_state_list = []  # DFA状态列表
    start = is_start.index(True)  # 起始状态
    start_closure = {start}  # 起始状态的闭包
    # update_epsilon_closure_dict(epsilon_transition)
    # print('epsilon_closure_dict',epsilon_closure_dict)
    epsilon_closure(epsilon_transition, start_closure)  # 计算起始状态的闭包
    end = has_end(start_closure, is_end)
    new_closure = DFA_State(start_closure, end, is_start=True)  # 创建新的DFA状态


    closure_list.append(new_closure)  # 将起始状态的闭包加入闭包列表
    dfa_state_list.append(new_closure)  # 将起始状态的闭包加入DFA状态列表
    # 将起始状态的闭包加入DFA状态列表
    while len(closure_list) > 0:  # 当闭包列表不为空时
        closure = closure_list.pop()  # 取出一个DFA(nfa闭包)
        for char in alnum_set:  # 遍历所有字符
            move_closure = move(closure.nfa_set, char, char_transition)  # 求到达闭包
            epsilon_closure(epsilon_transition, move_closure)  # 计算到达闭包的ε-闭包
            if not has_dfa_state(dfa_state_list, move_closure) and move_closure:  # 如果到达闭包不在DFA状态列表中,并且不为空
                end = has_end(move_closure, is_end)
                new_closure = DFA_State(move_closure, end)  # 创建新的闭包
                dfa_state_list.append(new_closure)  # 将到达闭包加入DFA状态列表
                closure_list.append(new_closure)  # 将新的闭包加入闭包列表
                closure.next[char] = new_closure.id  # 将新的闭包加入当前NFA的next列表
            elif has_dfa_state(dfa_state_list, move_closure):  # 如果到达闭包在DFA状态列表中
                closure.next[char] = find_dfa_id(dfa_state_list, move_closure)  # 将到达闭包加入当前闭包的next列表
    return dfa_state_list

最小化DFA： Hopcroft 算法

算法抽象

所谓自动机的化简问题即是对任何一个确定有限自动机DFA

M

$M$

，构造另一个确定有限自动机DFA

’

M’

$M ’$

，有

(

)

＝

(

’

)

L(M)＝L(M’)

$L (M) ＝ L (M ’)$

，并且

’

M’

$M ’$

的状态个数不多于M的状态个数，而且可以肯定地说，能够找到一个状态个数为最小的

’

M’

$M ’$

。

下面一些相关的基本概念。

设

S_i

$S_{i}$

是自动机M的一个状态，从

S_i

$S_{i}$

出发能导出的所有符号串集合记为

(

)

L(S_i)

$L (S_{i})$

。设有两个状态

S_i

$S_{i}$

和

S_j

$S_{j}$

，若有

(

)

＝

(

)

L(Si)＝L(Sj)

$L (S i) ＝ L (S j)$

，则称

S_i

$S_{i}$

和

S_j

$S_{j}$

是等价状态。

例如终态导出的符号串集合中必然包含空串ε，而非终止状态导出的符号串集合中不可能包含空串ε，所以终态和非终止状态是不等价的。

对于等价的概念，我们还可以从另一个角度来给出定义。

给定一个DFA

M

$M$

，如果从某个状态P开始，以字符串

w

$w$

作为输入，DFA

M

$M$

将结束于终态，而从另一状态Q开始，以字符串

w

$w$

作为输入，DFA M将结束于非终止状态，则称字符串

w

$w$

把状态P和状态Q区分开来。把不可区分开来的两个状态称为等价状态。

设

S_i

$S_{i}$

是自动机M的一个状态，如果从开始状态不可能达到该状态

S_i

$S_{i}$

，则称

S_i

$S_{i}$

为无用状态。

设

S_i

$S_{i}$

是自动机M的一个状态，如果对任何输入符号a都转到其本身，而不可能达到终止状态，则称

S_i

$S_{i}$

为死状态。

化简DFA关键在于把它的状态集分成一些两两互不相交的子集，使得任何两个不相交的子集间的状态都是可区分的，而同一个子集中的任何两个状态都是等价的，这样可以以一个状态作为代表而删去其他等价的状态，然后将无关状态删去，也就获得了状态数最小的DFA。

下面具体介绍DFA的化简算法：

首先将DFA M的状态划分出终止状态集K1和非终止状态集K2。

＝

∪

K＝K_1∪K_2

$K ＝ K_{1} \cup K_{2}$

由上述定义知，K1和K2是不等价的。

对各状态集每次按下面的方法进一步划分，直到不再产生新的划分。

设第

i

$i$

次划分已将状态集划分为

k

$k$

组，即：

＝

(

)

∪

(

)

∪

…

∪

(

)

K＝K_1(i)∪K_2(i)∪…∪K_k(i)

$K ＝ K_{1} (i) \cup K_{2} (i) \cup \dots \cup K_{k} (i)$

对于状态集

(

)

K_j(i)

$K_{j} (i)$

（j=1,2,…,k）中的各个状态逐个检查，设有两个状态

’

K_j’

$K_{j} ’$

、

’

K_j’’

$K_{j} ’ ’$

(

)

∈K_j(i)

$\in K_{j} (i)$

，且对于输入符号

a

$a$

，有：

（

′

）

＝

F（Kj’,a）＝K_m

$F （ K j^{'}, a ）＝ K_{m}$

（

”

，

）

＝

F（K_j”，a）＝K_n

$F （ K_{j} ” ， a ）＝ K_{n}$

如果

K_m

$K_{m}$

和

K_n

$K_{n}$

属于同一个状态集合，则将

’

K_j’

$K_{j} ’$

和

’

K_j’’

$K_{j} ’ ’$

放到同一集合中，否则将

’

K_j’

$K_{j} ’$

和

’

K_j’’

$K_{j} ’ ’$

分为两个集合。

重复第（2）步，直到每一个集合不能再划分为止，此时每个状态集合中的状态均是等价的。
合并等价状态，即在等价状态集中取任意一个状态作为代表，删去其他一切等价状态。
若有无关状态，则将其删去。

根据以上方法就将确定有限自动机进行了简化，而且简化后的自动机是原自动机的状态最少的自动机。

算法抽象伪代码如下：

←

−

Q/θ ← {F, Q − F}

$Q / θ \leftarrow F, Q - F$

2: while (

∈

∃U, V ∈ Q/θ, a ∈ Σ

$\exists U, V \in Q / θ, a \in Σ$

) s.t. Equation 1 holds do

←

(

−

)

∪

∩

−

(

)

−

∩

−

(

)

Q/θ ← (Q/θ − {U}) ∪ {U ∩ δ^{-1}(V, a), U − U ∩ δ^{-1}(V, a)}

$Q / θ \leftarrow (Q / θ - U) \cup U \cap δ^{- 1} (V, a), U - U \cap δ^{- 1} (V, a)$

4: end while

算法细化

具体的实现，我设计低阶API，中阶API，和高阶API进行实现

操作	说明	输入	输出
update_dfa_groupid	更新dfa的next	存放dfa的集合，存放dfa_group的集合	无
can_combine	判断两个dfa是否可以合并	dfa1的id，dfa2的id，存放dfa的集合	是否可以合并
is_unsplit_group	判断组内的dfa是否可以合并	一个dfa组，存放dfa的集合	是否该组内的dfa可以合并
not_min_dfa	判断最小化DFA是否已经结束	存放最小化dfa_group的集合，存放dfa的集合	是否结束
split_group	分组操作	一个dfa组，新的dfa组状态集合列表，存放dfa的集合	无
construct_dfa_group	封装 DFA组	存放dfa的集合，存放dfa组的集合	输出：dfa组的状态集合
minimize_dfa	dfa最小化	存放dfa的集合	最小化后的dfa组集合

关键操作伪代码如下

分组操作

    分组操作
    输入：一个dfa组，新的dfa组状态集合列表，存放dfa的集合
    split_group()函数将dfa组分成若干个子组，然后将子组加入到新的dfa组状态集合列表中
         子组列表=[]
        遍历dfa组中的dfa:
            如果子组列表为空:
                将dfa加入到子组列表中
            否则:
                遍历子组列表中的子组:
                    如果dfa可以和子组中的dfa合并:
                        将dfa加入到子组中
                        跳出循环
                否则:
                    将dfa加入到新的子组中
        将子组列表中的子组加入到新的dfa组状态集合列表中

封装DFA组

    封装 DFA组
    输入：存放dfa的集合，存放dfa组的集合
    输出：dfa组的状态集合
    construct_dfa_group()
        dfa组的状态集合=[]
        for dfa组 in dfa组集合:
            dfa组的状态集合列表.append(DFA组的状态(dfa组))
        return dfa组的状态集合

DFA最小化

dfa最小化
minimize_dfa()函数实现dfa最小化
输入：存放dfa的集合
输出：最小化后的dfa组集合

minimize_dfa()
    构造接受状态集合end_set和非接受状态集合not_end_set
    构造DFA组集合group_list
    将接受状态集合和非接受状态集合加入到DFA组集合中
    更新dfa组的id
    while 可以继续最小化:
        构造新的dfa组集合new_group_list
        for dfa组 in 原dfa组集合:
            if dfa组只有一个dfa:
                将dfa组加入到新的dfa组集合中
            else:
                分组操作
        更新dfa组的id
        
    封装dfa组
    return dfa组集合

判断是否已经最小化

    判断最小化DFA是否已经结束
    输入：存放最小化dfa_group的集合，存放dfa的集合
    输出：是否结束
    not_min_dfa()函数判断是否已经最小化
        for dfa组 in dfa组集合:
            if dfa组的长度不为1 and dfa组内的dfa不可以分割:
                return True
        return False

def minimize_dfa(dfa_state_list: list):
    # 1. 初始化

    # 1.1 构造接受状态集合
    end_set = set()
    for i in dfa_state_list:
        if i.is_end:
            end_set.add(i.id)
    # 1.2 构造非接受状态集合
    not_end_set = set()
    for i in dfa_state_list:
        if not i.is_end:
            not_end_set.add(i.id)

    # 1.3 构造状态集合列表
    group_list = list()
    if len(not_end_set) > 0:
        group_list.append(not_end_set)
    group_list.append(end_set)
    # print(group_list)

    # 2. 更新dfa_group_id
    update_dfa_groupid(dfa_state_list, group_list)
    # for i in dfa_state_list:
        # print(i.id,i.next_group_id)


    while (not_min_dfa(group_list, dfa_state_list)):  # 3. 判断是否满足最小化条件
        new_group_list = []  # 3.1 构造新的状态集合列表
        for group in group_list:  # 3.2 遍历状态集合列表
            if len(group) == 1:  # 3.2.1 如果集合中只有一个元素，直接加入新的状态集合列表
                new_group_list.append(group)
            else:
                split_group(group, new_group_list, dfa_state_list)
        group_list = new_group_list
        update_dfa_groupid(dfa_state_list, group_list)

    dfa_group_list = construct_dfa_group(dfa_state_list, group_list)

    return dfa_group_list

测试

每一个py文件可以单独测试

为验证算法的正确性，按照从简单到复杂的方式，设计了测试样例。

输入方式有四种：

在输入框输入
点击右边的按钮即可输入
点击随机按钮，可以随机生成输入
打开txt文件

验证方式：

answer1的56条经过手工计算和书本例子验证，结果一致
随机生成的测试样例相互测试

测试文件	来源	数据量
ansewr1.txt	人工设计(人工验算)	56条
answer2.txt	随机生成(符合语法)	1000条
i.txt	answer1中一条正则表达式	1条/文件

answer文件第1个数字为最小DFA的状态数量

界面右侧的测试样例

answer1.txt中部分测试样例

以ab(a|b)*为例子

NFA

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-V8aqaMwC-1666973145724)(实验2.assets/image-20221027194509465.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ewE0Caiv-1666973145724)(实验2.assets/image-20221027194528185.png)]

DFA

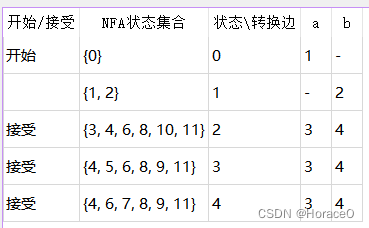
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-akstzyO8-1666973145725)(实验2.assets/image-20221027194556822.png)](https://img-blog.csdnimg.cn/b962b6833be14cbe86be3b680ba716e0.png)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EgJ43KjS-1666973145725)(实验2.assets/image-20221027194608932.png)]

最小化DFA

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hlHpQZQU-1666973145725)(实验2.assets/image-20221027194638122.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KK7Mt2Fg-1666973145725)(实验2.assets/image-20221027194648405.png)]

参考书的测试样例与本程序画的图

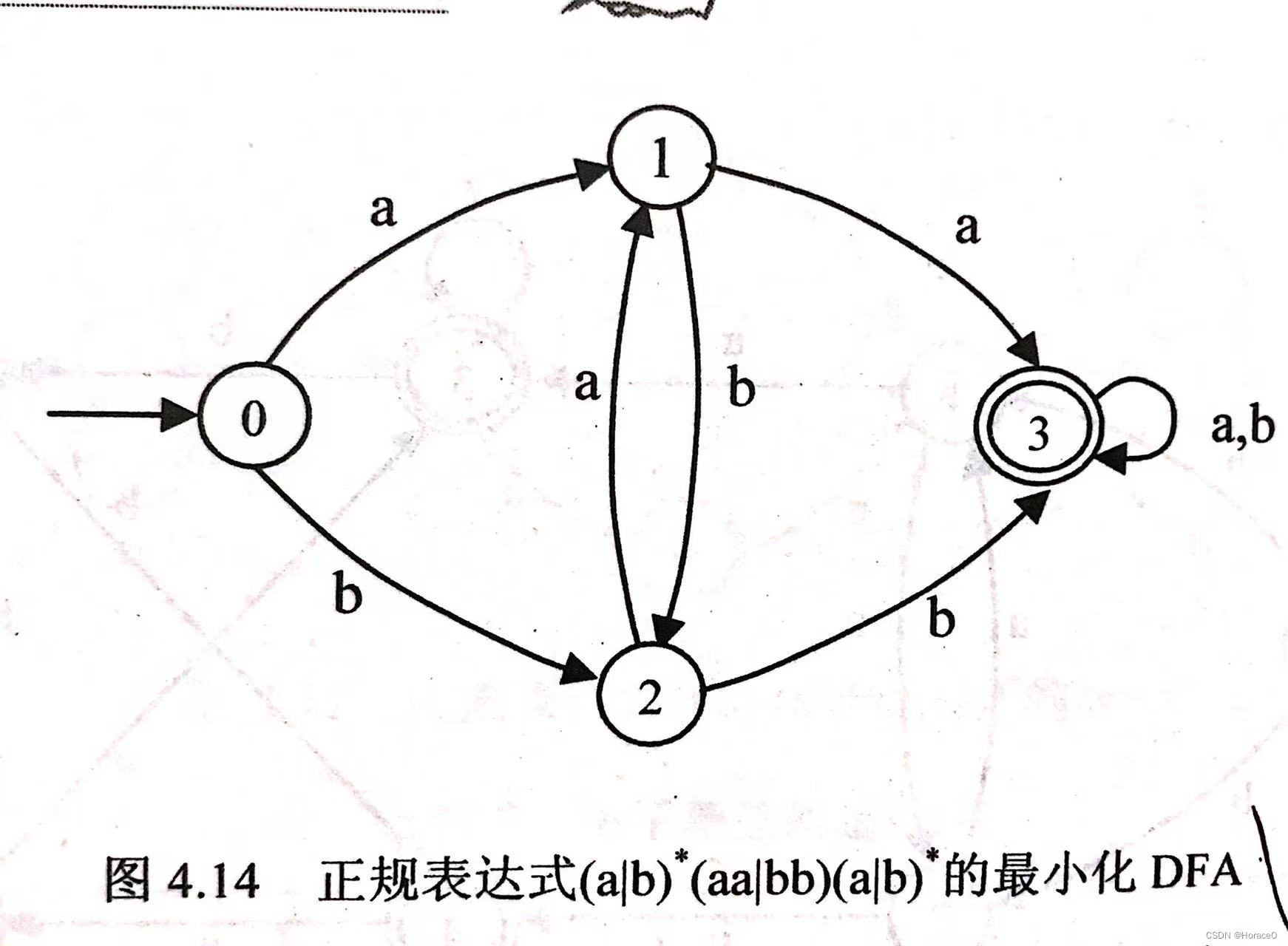
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qypJiQUD-1666973145726)(实验2.assets/image-20221027193709823.png)]

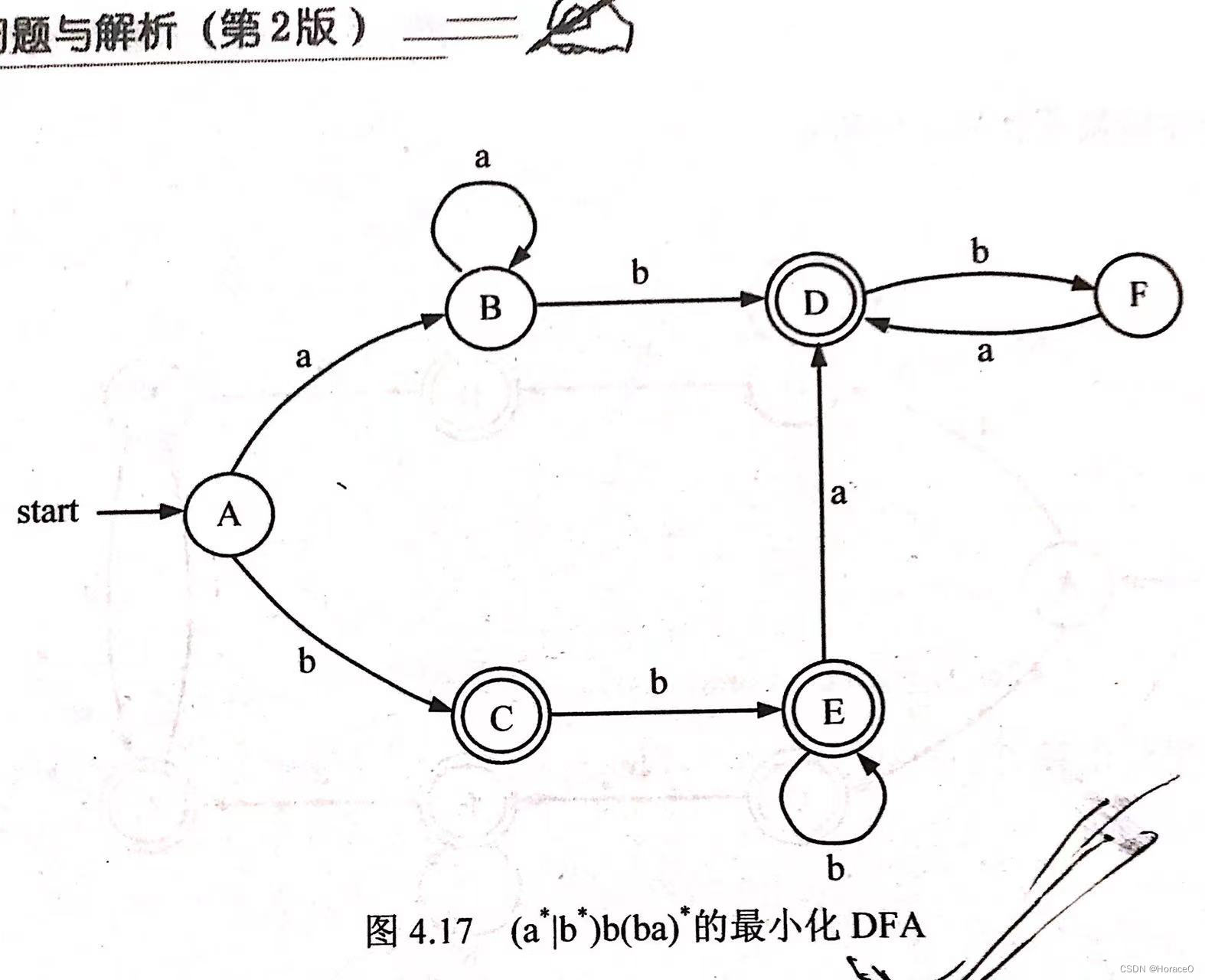
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-C5zujlnE-1666973145726)(实验2.assets/image-20221027193849251.png)][外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tNFcBY0v-1666973145726)(实验2.assets/94e2149c549cbbf4cf196931dd2078e.jpg)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-coTP1cYO-1666973145726)(实验2.assets/image-20221027193915870.png)][外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Meq4vkdb-1666973145727)(实验2.assets/68335a0419471fc81667367fce55feb.jpg)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CzSGpt45-1666973145727)(实验2.assets/image-20221027194156575.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fZ8U6rnY-1666973145727)(实验2.assets/image-20221027194300864.png)]

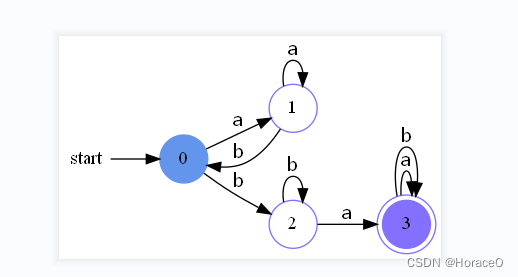
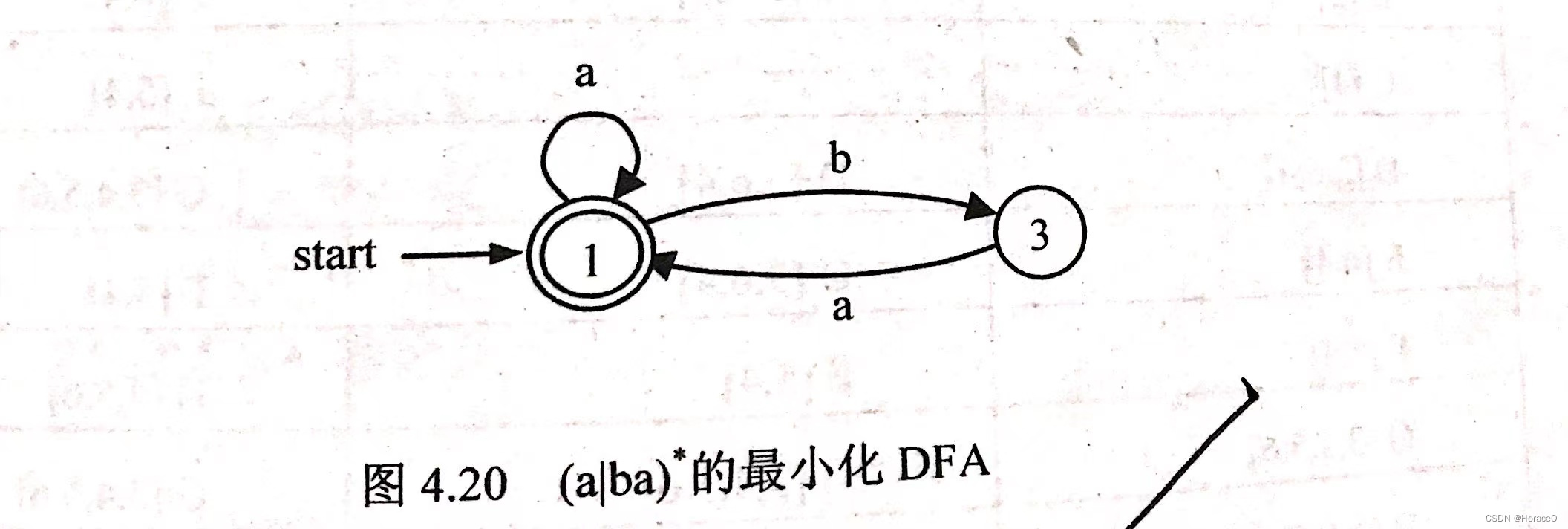
在这里插入图片描述

随机生成的1000条测试数据及结果，部分截图如下

若需完整代码，加个鸡腿，♪(･ω･)ﾉ v: L1220075670

备注(编译原理)

原文链接：https://blog.csdn.net/weixin_50094312/article/details/127581508