2020.10.26|COLING-2020|中国科学院大学|
原文链接
|
源码链接
TPLinker: Single-stage Joint Extraction of Entities and Relations Through Token Pair Linking
过去的方法:
联合学习可以获得明显的性能增益。 然而,它们通常涉及顺序的相互关联的步骤,并遭受暴露偏差的问题。 在训练时,他们根据地面真值条件进行预测,而在推理时,他们必须从头开始提取。 这种差异导致错误积累。
地面真值:在机器学习中,“ground truth”一词指的是训练集对监督学习技术的分类的准确性。这在统计模型中被用来证明或否定研究假设。“ground truth”这个术语指的是为这个测试收集适当的目标(可证明的)数据的过程。
论文中的方法:
握手标注方法
提出了一个单阶段联合提取模型TPLINKER,它能够发现共享一个或两个实体的重叠关系,同时不受暴露偏差的影响
基础准备
过去阶段一:把实体识别和关系抽取完全分离,容易造成级联错误
过去阶段二:联合学习整合实体和关系信息,使用基于解码器和基于分解的模型解决EPO和SEO,容易产生曝光偏差
基于编码器的:训练时,
地面真值令牌
被用作为上下文,推理时整个序列整个序列由最终模型自己生成,产生了训练和推理中预测的令牌是从不同的分布中提取的
基于分解的方法:在训练过程中使用
黄金实体
作为特定的输入来指导训练,在推理过程中输入的中心实体是由经过训练的模型给出的,导致了训练和推理之间的差距[黄金标准] 是经过注释的数据集(手动 或自动),然后手动更正。
该文章中的:
提出了一种用于实体和重叠关系联合提取的单阶段方法——TPLinker
将联合抽取任务转化为令牌对链接的问题,TPLinker将被用于回答以下问题:
前提条件:给出一个句子、两个位置P1\P2和一个特定关系R
- “P1和P2是否分别是同一个实体的开始和结束位置”
- “P1和P2是否分别是两个具有R关系的实体的开始位置”
- “P1和P2是否分别是两个具有R关系的实体的结束位置”
实施:为每个关系标注了三个令牌链接矩阵,利用这三个令牌链接矩阵回答上述三个问题,然后利用这些矩阵对不同的标注结果进行解码,提取所有实体和重叠关系。
效果:不包含任何相互依赖的提取不走,实现了训练和测试的一致性
方案详解:
握手标记方案:
普通矩阵方案:
通过用链接标记方法进行标记令牌对,实现了一步联合抽取

如上图,给定一个句子,枚举所有可能的令牌对,病使用矩阵标记令牌链接,但是有以下问题:
是
稀疏矩阵
,由于实体尾部不可能出现在实体头部之前,所以下三角区域的标签都是零,这是对内存的巨大浪费。但是,目标实体可能出现在相应的主体实体之前,这意味着直接将下三角区域降下来是不合理的。
三种类型的链接定义:
实体头到实体尾(EH-to-ET)
。 矩阵中的紫色标记是指对应的两个位置分别是
一个实体的开始和结束令牌
。 例如,“New York CIty”和“de Blasio”是句子中的两个实体,因此,标记对(“new”,“city”)和(“de”,“Blasio”)被赋予紫色标记1。
主体头到客体头(SH-to-OH)
。 红色标签表示两个位置分别是
成对的主体实体和对象实体的开始令牌
。 例如,“New York CIty”和“de Blasio”之间存在“mayor”关系,因此标记对(“new”和“de”)被分配为红色标记1。
主语尾到宾语尾(ST-to-OT)
。 蓝色标签与红色标签具有类似的逻辑,这意味着两个位置
分别是成对的主体实体和对象实体的结束标记
。 例如,标记对(“City”、“Blasio”)被分配蓝色标记1。
握手矩阵方案:
将
下三角区域
中的所有
标签1
映射到
上三角区域中
的
标签2
,然后删掉下三角区域。为了张量计算方便,将剩下的项压缩成一个序列,即总框架图中的橙色序列,并
用一个映射记住原矩阵中的位置
,类似于所有令牌中的握手,故称为握手矩阵。
存在的问题
:该方案不能处理EPO问题,因为对于同一实体对,不同的关系不能在同一矩阵中标记在一起。
解决方法
:我们为每种关系类型做同样的矩阵标记工作。

构造矩阵进行标注:
联合抽取任务被解构为
2
N
+
1
2N+1
2
N
+
1
个序列标记子任务,其中N表示预定义关系类型的数量,每个子任务建立一个长度为
n
2
+
n
2
\frac{n^2+n}{2}
2
n
2
+
n
的标记序列,其中
n
n
n
表示输入句子的长度。
存在的问题
:标签序列的长度随着句子长度的增加而以平方的形式增加,比较抵消
解决方法
:再编码器的顶部使用轻量级标记模型,TPLinker在效率上可以与最先进的模型与之媲美。因为,编码器被所有标记起共享,只需要生成n个令牌表示一次
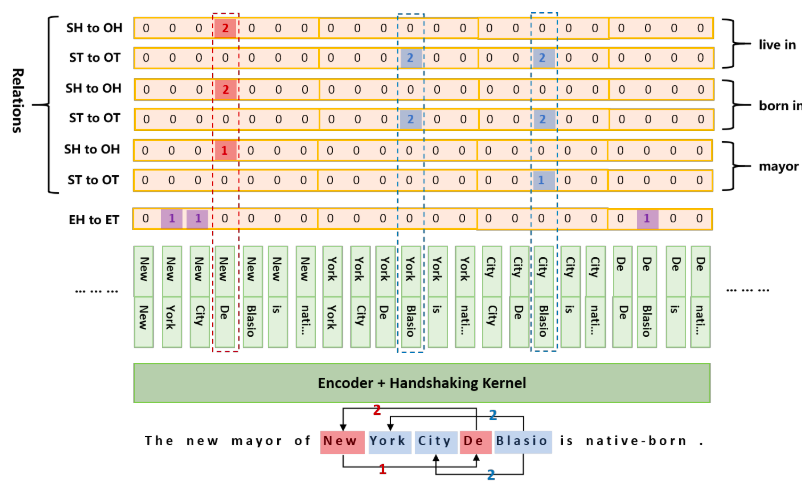
解码:
- (“new”,“york”)、(“new”,“city”)和(“de”,“blasio”)在EH-to-ET序列中标记为1
-
“new york”、“new york city”和“de blasio”是三个实体
- 对于关系“mayor”,(“new”、“de”)在SH-to-OH序列中标记为1
-
“new”开头的主语的mayor是以“de”开头的宾语
- (“City”、“Blasio”)在ST-to-OT序列中标记为1
-
主语和宾语分别是以“City”和“Blasio”结尾的实体
-
由此,
可以解码出一个三胞胎:(“New York City”,Major,“Blasio”)
标记2与标记1的含义相反,表示令牌之间的反向链接,因为矩阵中反转了
在关系“born in”的ST-to-OT序列中(“York”、“Blasio”)标记为2,这意味着“York”和“Blasio”分别是
成对的宾语和主语的尾部
结合其他两个序列,解码后的应该是(“Blasio”,“born in”,“York”)。
对于每一个关系
-
首先从
EH-to-ET序列
中提取所有的
实体
跨度,将每个头位置映射到
以该位置为起点的相应实体
存入字典D -
对于每一个关系,首先从
ST-to-OT
序列中解码(主题尾位置,宾语尾位置)元组并将其
添加到集合E
中,然后从
SH-to-OH
序列中解码(主题头位置,宾语头位置)元组并查找
字典D中以头位置为起点
的所有可能的实体。 -
我们迭代
所有候选主宾对
,以检查它们的尾位置是否在E中。如果是,则提取一个新的三元组并添加到
结果集T
中。
令牌对表示:
h
i
,
j
=
t
a
n
h
(
W
h
⋅
[
h
u
;
h
j
]
+
b
h
)
,
j
≥
i
(1)
h_{i,j} = tanh(W_h\cdot[h_u;h_j] + b_h),j \geq i \tag{1}
h
i
,
j
=
t
anh
(
W
h
⋅
[
h
u
;
h
j
]
+
b
h
)
,
j
≥
i
(
1
)
长度为n的句子
[
w
1
,
.
.
.
.
,
w
n
]
[w_1,….,w_n]
[
w
1
,
….
,
w
n
]
,通过基本编码器将每个令牌wi映射到一个低维的上下文向量
h
i
h_i
h
i
中,燃火可以生成
h
i
,
j
h_{i,j}
h
i
,
j
来表示令牌对
(
w
i
,
w
j
)
(w_i, w_j)
(
w
i
,
w
j
)
W
h
W_h
W
h
是矩阵的参数,
b
h
b_h
b
h
是要需要训练的偏差向量,
在总架构图中称为握手内核
握手标记器
使用统一的架构来标记三种类型的链接,给出令牌对
h
i
,
j
h_{i,j}
h
i
,
j
由公式3预测令牌对
(
w
i
,
w
j
)
(w_i, w_j)
(
w
i
,
w
j
)
P
(
y
i
,
j
)
=
S
o
f
t
m
a
x
(
W
o
⋅
h
i
,
j
+
b
o
)
(2)
P(y_{i,j}) = Softmax(W_o \cdot h_{i,j} + b _o) \tag{2}
P
(
y
i
,
j
)
=
S
o
f
t
ma
x
(
W
o
⋅
h
i
,
j
+
b
o
)
(
2
)
l
i
n
k
(
w
i
,
w
j
)
=
a
r
g
max
l
P
(
y
i
,
j
=
l
)
(3)
link(w_i, w_j) = arg\max_lP(y_{i,j} = l) \tag{3}
l
ink
(
w
i
,
w
j
)
=
a
r
g
l
max
P
(
y
i
,
j
=
l
)
(
3
)
其中
P
(
y
i
,
j
=
l
)
P(y_{i,j} = l)
P
(
y
i
,
j
=
l
)
表示为将
(
w
i
,
w
j
)
(w_i, w_j)
(
w
i
,
w
j
)
识别为
l
l
l
的概率
握手序列编码器的伪代码:

损失函数
L
l
i
n
k
=
−
1
N
∑
i
=
1
,
j
≥
i
N
∑
∗
⊂
{
E
,
H
,
T
}
log
P
(
y
i
,
j
∗
=
l
∗
^
)
(4)
L_{link} = – \frac {1}{N} \sum_{i=1, j \geq i}^{N} \sum_{* \subset {\lbrace E, H, T \rbrace}}\log P(y_{i,j}^* = \hat{l^*}) \tag{4}
L
l
ink
=
−
N
1
i
=
1
,
j
≥
i
∑
N
∗
⊂
{
E
,
H
,
T
}
∑
lo
g
P
(
y
i
,
j
∗
=
l
∗
^
)
(
4
)
这里,
N
N
N
是输入句子的长度,
l
∗
^
\hat{l^*}
l
∗
^
是真标记,
E
、
H
E、H
E
、
H
和
T
T
T
分别表示eh-to-et、sh-to-oh和st-to-ot的标记器。
实验对比
数据集准备
NYT和WebNLG作为数据集

使用Precision、Recall、F1-score作为评判标准
基线对比
(以下为原文)

- Tplinker在注释最后一个单词的数据集和注释整个跨度的数据集上都表现良好
- 在NYT和NYT*上的得分几乎相同,这也表明只注释最后一个单词的数据集并不总是比注释整个跨度的数据集容易。 甚至相反,这可能会更难,因为不同的实体可能共享相同的最后一个词,这使得重叠情况的数量增加。
- WebNLG和WebNLG* 的性能之间存在明显的差距,但发现WebNLG中有127个错误的三元组,包含一个无意义的空实体。 另外,webnlg有216个关系,而webnlg* 只有171个。可能是这些原因造成,为比较,不解决
-
- WebNLG* 的性能已经饱和,因为提取含有171个预定义关系的三元组非常困难,尤其是训练数据很少(5019句)。 这些方法获得了90+F1的分数,可能已经超过了人类水平的表现。 换言之,提振空间太有限。
-
-
WebNLG* 中的许多关系具有相同的含义,如LeaderName和Leader,affiliation和affiliations,这给模型带来了混乱。 在许多情况下,我们的模型将提取它们两个,但通常只有其中一个在测试集中被注释。由于
TP
L
i
n
k
e
r
b
e
r
t
TPLinker_{bert}
TP
L
ink
e
r
b
er
t
模型具有较强的提取重叠关系的能力和较好的查全率,因此这些正确注释的缺失严重影响了Tplinkerbert模型的查全率。
-
WebNLG* 中的许多关系具有相同的含义,如LeaderName和Leader,affiliation和affiliations,这给模型带来了混乱。 在许多情况下,我们的模型将提取它们两个,但通常只有其中一个在测试集中被注释。由于
知识补充
- 序列标注:
- 序列标注是一个比较简单的NLP任务,也可成为最基本的任务。序列标注是给定一个输入序列,使用模型对这个序列的
每一个位置标注一个相应的标签
,是一个序列到序列的过程。序列标注的涵盖范围非常广,可以解决一系列对字符进行分类的问题,如分词、词性标注、命名实体识别、关系抽取等。
- 序列标注可分
原始标注
和
联合标注
,原始标注就是
每个元素
中都需要被标注的一个标签,联合标注就是所有的
分段
都被标注为同样的标签,命名实体识别是信息提取问题中的一个子任务,需要将元素进行定位和分类,如人名、地点、时间、组织名、质量等。- BIO标注:解决联合标注问题的最简单的方法,就是将其转化为原始标注问题,即使用BIO标注。
- BIO标注是将每个元素标注为
“B-X”、“I-X”或者“O”
。其中,
“B-X”
表示此元素所在的片段属于
X类型
并且此元素为词片段的
起始词
,
“I-X”
表示此元素所在的片段属于
X类型
并且此元素为词片段的
起始词之后的词
,
“O”
表示该字
不属于
事先定义的任何词片段类型。- 常用的序列标注还有BIOES标注和BMES标注。
- BIOES标注主要将多元实体X标注为
B-X,I-X,E-X
的格式,
B-
:实体的
开头
,
I-
:实体的
中间
;
0-
:
非实体
部分;
E-
:
实体的结尾
;
S-
:
单个字符,其本身就是一个实体
。
- BMES标注中的
B-
:实体的
开头
,
M-
:实体的
中间
,
O-
:非实体
部分
,
E-
:实体的
结尾
、
S-
:
单个字符,其本身就是一个实体
。
可以看出在很多任务以上各种标注体系的表现差异不大。
- BERT: BERT:双向Transformer的Encoder