博客

BookRead 矩阵变换深度理解 – 《3D数学基础 ：图形与游戏开发》

坐标系系统介绍

多坐标系

向量

矩阵

齐次矩阵

矩阵和线性变换概述

矩阵变换的理解

矩阵变换的理解（0）- 变换物体与变换坐标系

矩阵变换的理解（1）- 假设点的位置在不同坐标系中是不变的

矩阵变换的理解（2）- 假设点的位置随着坐标变换而变换

矩阵变换的理解（3）- 以旋转为例

注意：这本书中使用到的坐标系是左手坐标系，并且向量的空间变换是右乘矩阵实现，即向量 x 矩阵

同时本篇内容相对于其他相关文章的区别是，加入了个人对于矩阵变换的一些理解，其他详细的读书笔记可以参见这篇博文：https://blog.csdn.net/sinat

24229853/category

5643379.html

坐标系系统介绍

笛卡尔坐标系是就是直角坐标系和斜坐标系的统称。如下图所示：

直角坐标系，坐标系的轴之间都是垂直的，否则就是斜角坐标系。

除了笛卡尔坐标系之外还有其他的坐标系，如极坐标系，如下图所示：

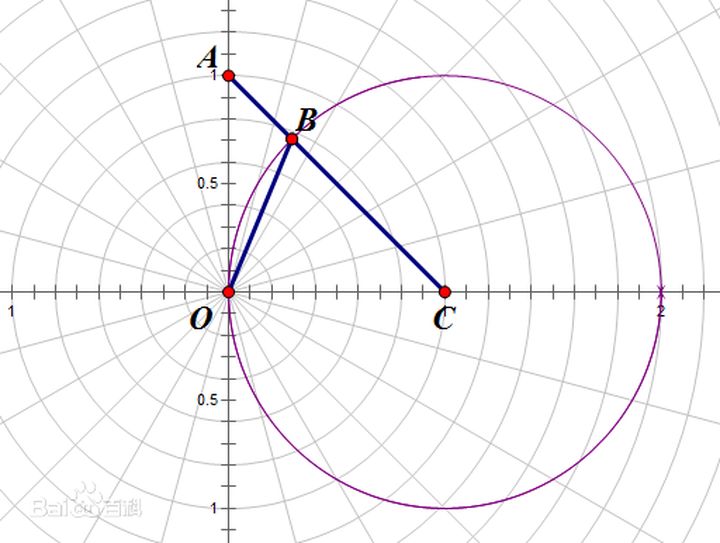
3D渲染，图形处理里面用的最多的就是笛卡尔坐标系。

多坐标系

• 
  世界坐标系
  
  ：一个特殊的坐标系，通常意义上理解，能够用世界坐标系描述其他坐标系的位置，而不能用更大的，外部的坐标系来描述世界坐标系；需要关注的点包含：
  • 世界坐标系中，每个物体的位置；
  • 观察这个世界的相机的位置和方向；
  • 各个物体的移动规律；
• 
  模型坐标系（物体坐标系）
  
  ：每个物体都有自己的独立坐标系，当物体移动或改变方向时，和该物体相关联的坐标系随之移动或改变方向；比如行走是的向前走一步，此时坐标系在人自己上；需要关注的点包含：
  • 周围有需要相互作用的物体么？
  • 相对于你的那个方向？
• 
  摄像机坐标系
  
  ：想象带着一个相机在拍照，这个时候需要关心的包括：
  • 相机能够拍到哪些物体；
  • 相机看