博客

栈（stack）与队列（queue）

  • Post author:
  • Post category:其他


文章目录




栈（stack）





栈是什么


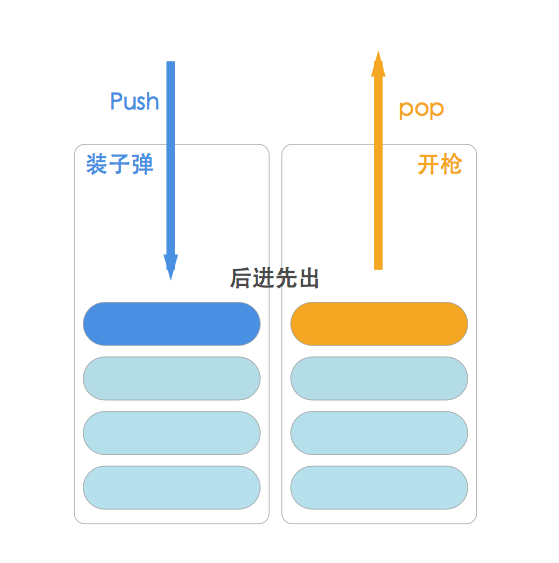
栈（stack）是限制对元素的插入（push）和删除（pop）只能在一个位置上进行的表，该位置是表的末端，叫做栈的栈顶（top)。

初次理解栈，你可以把它理解为一种特殊的数组，元素在栈顶添加和删除。栈类似于弹夹，最后装进去的元素最先取出来，这也是栈遵循的后进先出（LIFO——Last-In-First-Out）原则。

请添加图片描述




栈的优势


栈的操作是常数时间的，而且是以非常快的常数时间。在某些机器上，push和pop都可以写成一条机器指令，现代计算机把栈操作作为它指令的一部分。因此栈是在计算机科学中继数组之后最基本的数据结构。




栈的实现


栈的几个基本函数：


  • push

    ：添加元素到栈顶，返回是否成功添加

  • pop

    ：删除位于栈顶的元素，返回是否成功删除

  • peek

    ：返回栈顶元素

  • isEmpty

    ：判断当前栈是否为空

  • isFull

    ：判断当前栈是否已满

  • size

    ：返回栈的元素个数

  • clear

    ：清空栈

栈可以通过顺序存储和链式存储两种结构分别实现。




栈的顺序存储



  • 栈的定义
     
typedef struct arrayStack {
    int data[MaxSize];	// 存储元素的数组
    int top;			//栈顶指针
}ArrayStack;

为了方便理解，这里的数据储存类型为int。一般情况下，我们给int起一个别名，这样就这样实现简单的多态，需要将int类型栈改成其他类型栈时，只需要改定义别名的类型即可。


  • push

    ：添加元素到栈顶，并返回是否成功添加 
bool push(ArrayStack *arrayStack, int element) { 
	if (arrayStack.top == MaxSize - 1) {			// 栈满
        return false;
    }
	arrayStack.data[arrayStack.top] = element;	// 加入栈中
    arrayStack.top++;								//栈顶指针+1
    return true;
}

  • pop

    ：删除位于栈顶的元素，返回是否成功删除 
bool pop(ArrayStack *arrayStack) {	
     if(arrayStack.top == 0) {							// 栈空
         return false;
    }
    arrayStack.top--;									//栈顶指针-1
    arrayStack.data[arrayStack.top] = 0;				//重置栈顶元素
    return true;
}

  • peek

    ：返回栈顶元素 
int peek(ArrayStack *arrayStack) {	
     if(arrayStack.top == 0) {					//栈空
         return 0;
    }
    return arrayStack.data[arrayStack.top - 1];	//返回栈顶元素
}

  • isEmpty

    ：判断当前栈是否为空 
BOOL isEmpty(ArrayStack *arrayStack) {	
     if(arrayStack.top == 0) {	//栈空
         return 0;
    } else {					//栈不为空
    	return 1;
    }
}

  • isFull

    ：判断当前栈是否已满 
BOOL isFull(ArrayStack *arrayStack) {	
	if(arrayStack.top == MaxSize - 1) {	//栈满
         return 1;
    } else {							//栈未满
    	return 0;
    }
}

  • size

    ：返回栈中元素个数 
int size(ArrayStack *arrayStack) {	
	return arrayStack.top;	//返回栈顶指针
}

  • clear

    ：清空栈 
void clear(ArrayStack *arrayStack) {	
	int n = arrayStack.top;
	while(n) {						//重置栈中元素
		arrayStack.data[n - 1] = 0;
		n--;
	}
	arrayStack.top = 0;				//重置栈顶指针
}




栈的链式存储



  • 栈的定义
     
typedef struct linkedStack {
    int data;				//数据域
    struct linkedStack *next;	//指针域
}LinkedStack;

  • push

    ：添加元素到栈顶 
void push(LinkStack *top, int element) {
    LinkedStack *node = (LinkedStack)malloc(sizeof(LinkedStack));	//创建新结点
    node->data = element;   										//给结点数据域赋值
    node->next = top->next;											//将结点入栈
    top->next = node;
}

注意：链表形式的栈不可能栈满，故push不用判断栈满情况


  • pop

    ：删除位于栈顶的元素，并返回是否成功删除 
bool pop(LinkedStack *top) {	
     if(top->next == NULL) {		//栈空判断
        return false;
    }
    LinkedStack *node = top->next;	//标记pop结点
    top->next = node->next;			//删除该结点
    free(node);
    return true;

  • peek

    ：返回栈顶元素 
int pop(LinkedStack *top) {	
     if(top->next == NULL) {	//栈空判断
        return 0;
    }
    return top->next->data;

  • isEmpty

    ：判断当前栈是否为空 
BOOL isEmpty(LinkedStack *top) {	
     if(top->next == NULL) {	//栈空
         return 0;
    } else {				//栈不为空
    	return 1;
    }
}

  • size

    ：返回栈中元素个数 
int size(LinkedStack *top) {	
	int cnt = 0;				//计数器
	while(top->next != NULL) {	//每有一个结点就让计数器+1
		cnt++;
		top = top->next;
	}
	return cnt;
}

  • clear

    ：清空栈，释放内存空间 
void clear(LinkedStack *top) {
	LinkedStack *front = top;	//设置前后结点
   	LinkedStack *rear;
    while (front) {				//判断是否移动到队尾
        rear = front;
        front = front->next;
        free(rear);
    }
}




队列（queue）





队列是什么


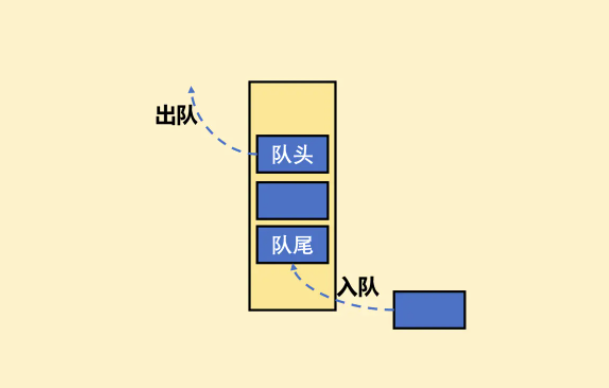
队列，又称为伫列（queue），是先进先出（FIFO——First-In-First-Out）的线性表。在具体应用中通常用链表或者数组来实现。队列只允许在后端（rear）进行插入操作，在前端（front）进行删除操作。

队列，顾名思义，就像排队一样，先入队的先出队，队内的元素不能插队也不能中途退出。

在这里插入图片描述




队列的实现


队列同样可以用顺序存储和链式存储两种结构来表示。




队列的顺序存储



  • 结构体定义
     
typedef struct {
    int data[MaxSize];	//用静态数组存放队列元素
    int front;			//队头指针
    int rear;		    //队尾指针
}ArrayQueue;

我们仿照顺序存储栈时的做法，并添加了对头和队尾指针。在初始状态，我们将队头、队尾指针指向0。在操作队列的过程中，我们保证队头指针指向队头的下标，队尾指针指向队尾的下一个位置。

有了这些规则后，我们对一个长度为6的队列进行5次入队，5次出队操作：

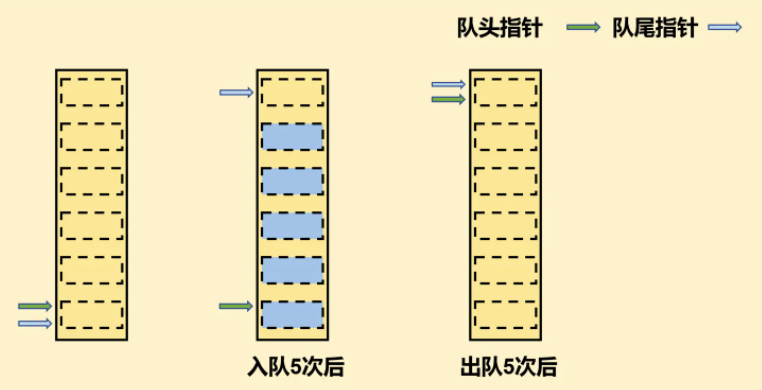
在这里插入图片描述

考虑该情况下如何判断队满，容易想到，判断尾指针是否等于MaxSize – 1即可。但是这样做有个很明显的问题，当我们对一个MaxSize = 6的队列，入队5次再出队5次后，我们的尾指针等于MaxSize – 1，但是我们队列其实是空的，内存空间没有得到充分利用。为了解决这个问题，我们采用

循环队列

这种逻辑结构。

在物理上，我们还是使用一个连续的数组来存储。在逻辑上我们数组的末尾和数组开头是连续的。当循环队列的队尾指针到达数组末尾后，会重新回到数组起始位置，实现了对内存的重复利用。
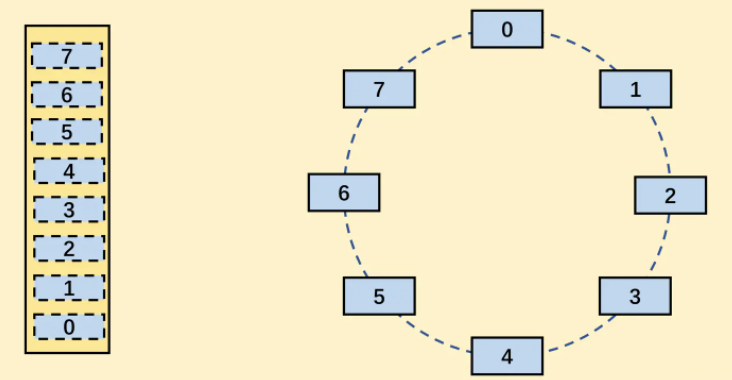
在这里插入图片描述

需要注意的是，在移动队头、队尾指针时，我们需要对 MaxSize 取模，以达到正确的移动。如对一个 MaxSize = 8 的队列，当队头指针到达7时，再添加元素入队，此时队头指针的位置应该是 (7 + 1) % 8 = 0，回到数组下标为0的位置。因此，移动队头、队尾指针的操作应该为：

front->front = (front->front + 1) % MaxSize;

front->rear = (front->rear + 1) % MaxSize;

下面是循环队列的核心函数。


  • initQueue

    ：队列初始化 
void initQueue(ArrayQueue *queue){
    queue->front = queue->rear = 0;	//重置头尾指针即完成了队列的初始化
}

  • isEmpty

    ：判断队列是否为空 
bool isEmpty(ArrayQueue *queue){
    if (queue.rear == queue.front) {	//队尾指针和队头指针重合即为队空
    return true;
    } else {
    return false;
    }
}

  • enQueue

    ：将元素加入队列，并返回是否成功入队 
int enQueue(ArrayQueue *queue, int element) {
    if((queue->rear + 1) % MaxSize == queue->front) {	//队满
        return false;
    }
    queue->data[queue->rear] = element;					//将元素插入队尾
    queue->rear = (queue->rear + 1) % MaxSize;			//移动队尾指针
    return true;
}

  • deQueue

    ：令队尾元素退出队列，并返回是否成功出队 
int deQueue(ArrayQueue *queue) {
    if (isEmpty(queue)) {							//队空
        return false;
    }
    queue->front = (queue->front + 1) % MaxSize;	//移动队头指针
    return true;
}




队列的链式存储


  • 结构体定义 
typedef struct queueNode {		//链式队列结点
    int data;
    struct queueNode *next;
}QueueNode;

typedef struct {
    Queue *front;	//队头指针
    Queue *rear;	//队尾指针
}LinkedQueue;

  • initQueue

    ：队列初始化 
void initQueue(LinkedQueue *queue) {
    queue->front = (LinkedQueue *)malloc(sizeof(LinkedQueue));
    queue->rear = (LinkedQueue *)malloc(sizeof(LinkedQueue));
    queue->front->next = NULL;	//初始化队头指针
    queue->rear->next = NULL;	//初始化队尾指针
}

  • isEmpty

    ：判断队列是否为空 
bool isEmpty(LinkedQueue *queue) {
    if (queue.rear == queue.front) {	//队尾指针和队头指针重合即为队空
    return true;
    } else {
    return false;
    }
}

  • enQueue

    ：将元素加入队列 
void enQueue(LinkedQueue *queue, int element) {
    QueueNode *node = (QueueNode *)malloc(sizeof(QueueNode));	//创建结点
    node->data = element;		//结点初始化
    node->next = NULL;
    queue->rear->next = node;	//在队尾插入结点
    queue->rear = node;			//移动队尾指针
}

  • deQueue

    ：令队尾元素退出队列，并返回是否成功出队 
bool deQueue(LinkedQueue *queue) {
    if (isEmpty(queue)) {					//队空
        return false;
    }
    QueueNode *node = queue->front->next;	//标记要出队的元素
    queue->front->next = node->next;		//移动队头指针
    if (queue->rear == node) {				//如果最后一个元素出队，则需要修改队尾指针
        queue->rear == queue->front;
    }
    free(node);
    return true;
}

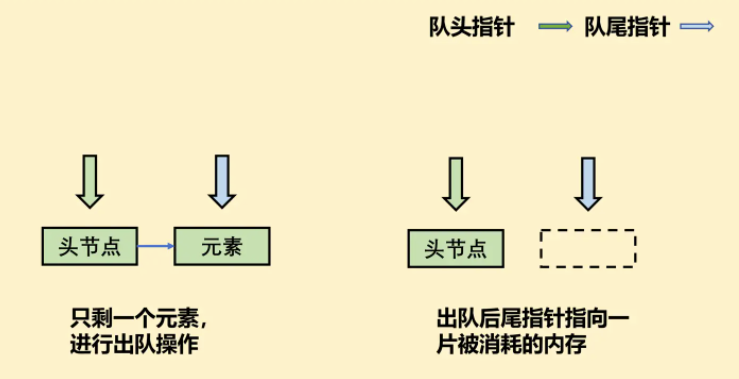
deQueue对于最后一个元素出队的情况有特殊处理，因为当我们删除最后一个结点后，队尾指针指向了一片已经销毁的内存。且队列为空时，头尾指针应该相同。因此我们需要在删除最后一个节点后，令队尾指针等于队头指针。

判断最后一个元素的条件：头节点（queue.front）的next是否是尾节点。

在这里插入图片描述


  • destroyQueue

    ：销毁链式储存队列，释放内存空间 
void destroyQueue(LinkedQueue *queue) {
    QueueNode *front = queue->front;	//设置前后结点
   	QueueNode *rear;
    while (front) {						//判断是否移动到队尾
        rear = front;
        front = front->next;
        free(rear);
    }
}




若干应用





删除字符串中的所有相邻重复项


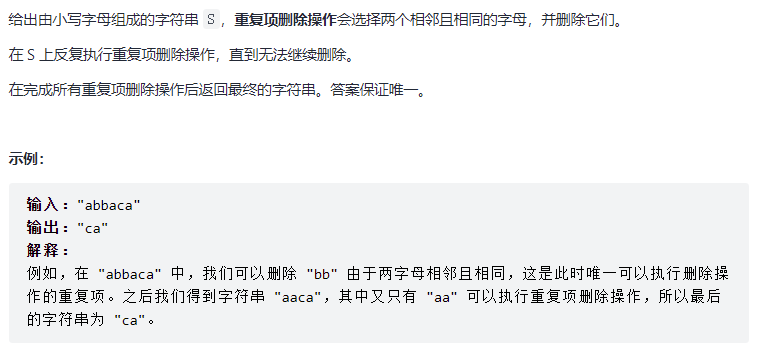
在这里插入图片描述

这题的题目描述很像“祖玛”游戏，碰到相同的珠子就消去，只留下不相同的。

在这里插入图片描述

我们可以利用栈的思想来解决这道题。将每个字符入栈，当栈顶字符与当前字符一样时，就将栈顶字符弹出；若不一样，则正常入栈。

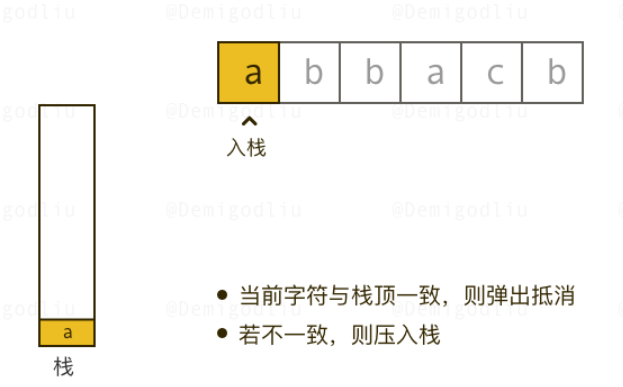
在这里插入图片描述 

char *removeDuplicates(char *s) {
    int d = strlen(s);
    char *stack = malloc(sizeof(char) * (d + 1));
    int p = 0;
    for (int i = 0; i < d; i++) {
        if (p > 0 && stack[p - 1] == s[i]) {
            p--;
        } else {
            stack[p++] = s[i];
        }
    }
    stack[p] = '\0';
    return stack;
}




有效的括号


在这里插入图片描述

这道题让我们验证输入的字符串是否为括号字符串，包括大括号，中括号和小括号。对于这个问题，我们依然可以利用栈：

遍历输入字符串，如果当前字符为左半边括号，则将其压入栈中。遇到右半边括号，若此时栈为空，则直接返回false；如不为空，则取出栈顶元素，若为对应的左半边括号，则继续循环，反之返回false。当所有括号都验证完了，就返回true，此时字符串s就是“有效的括号”。

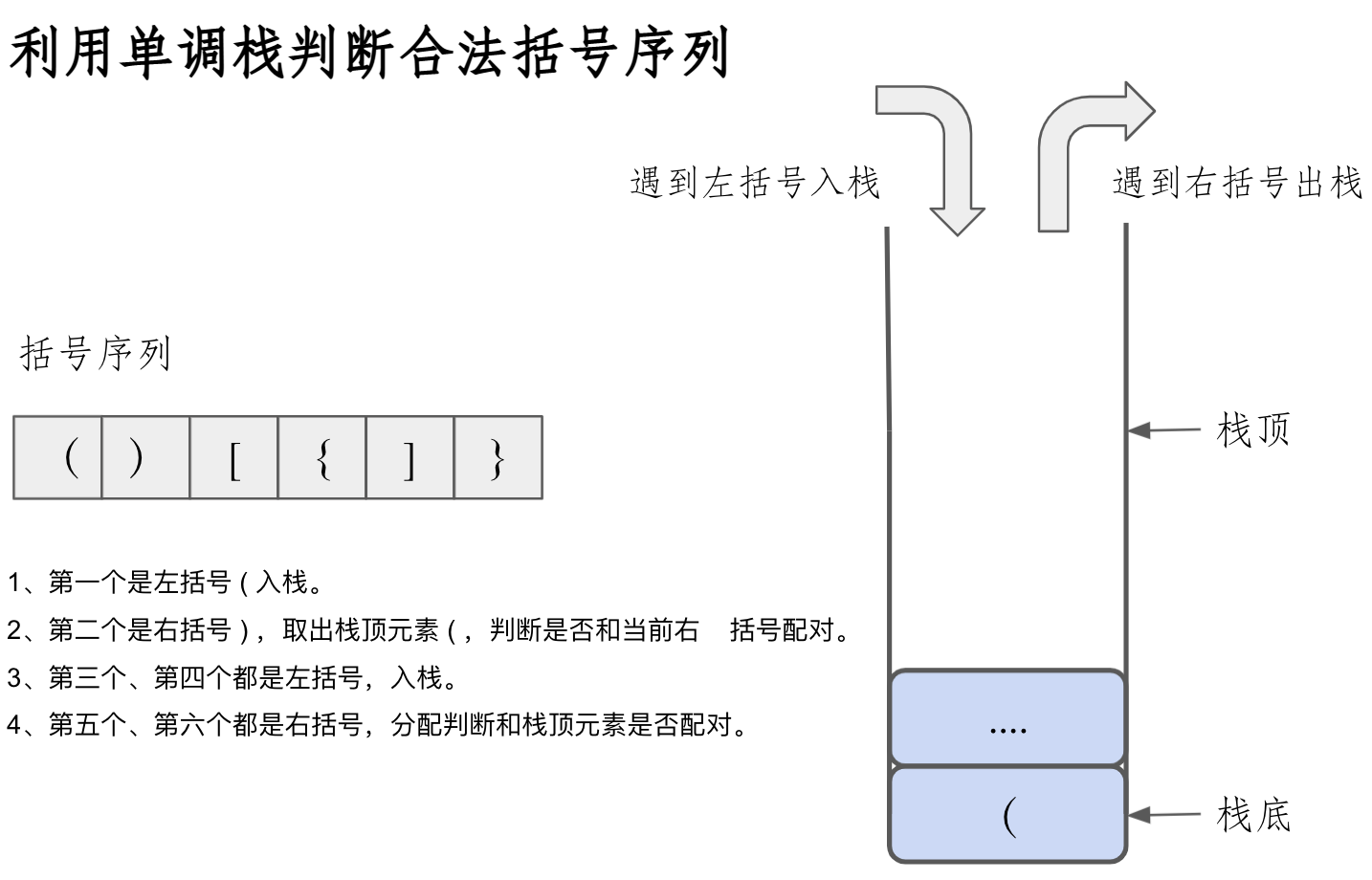
在这里插入图片描述 

bool isValid(char *s) {
    if (!s) {
    return true;
    }
    int d = strlen(s);												//字符串长度											
    char *stack = (char *)malloc(sizeof(char) * (d + 1));			//创建栈
    int p = 0;
    for (int i = 0; i < d; i++) {
        if (s[i] == '(' || s[i] == '[' || s[i] == '{') {			//左括号入栈
            stack[++p] = s[i];
        }else if (s[i] == stack[p] + 1 || s[i] == stack[p] + 2) {	//右括号找对应左括号
        p--;
        }
        else {
        return false;
        }
    }
    if (p) {
    return false;
    } else {
    return true;
    }
}




马踏棋盘问题


将马放到国际象棋的8 * 8棋盘上的任意指定方格中，按照“马”的走棋规则将“马”进行移动，要求每个方格进入且只进入一次，走遍棋盘上的64个方格，将数字1,2,3…,64依次填入一个8 * 8的方阵。

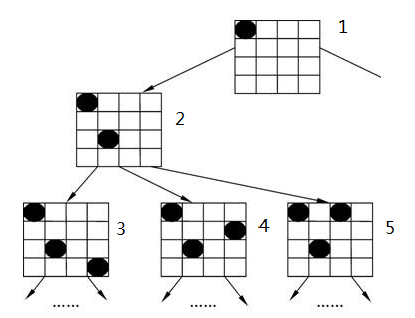
在这里插入图片描述

我们可以采用深度优先法求解，深度优先搜索是指对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。

如图所示，当马在当前位置时(节点１)，将它下一跳的所有位置看作分支结点，然后选择一个分支结点进行移动，如节点２，然后再走该结点的分支结点，如节点３，如果节点３不能再走下去，则退回到节点２，再选择另一种走法，如节点４，一直走下去，直至不能派生出其他的分支结点，也就是“马”走不通了。此时则需要返回上一层结点，顺着该结点的下一条路径进行深度优先搜索下去，直至马把棋盘走遍。

这和栈有什么关系呢？其实在回溯的过程中，就可以利用栈的模型。从起点开始(如节点１)，将走过的位置全部入栈（如节点2、3）。当走到节点3发现无路可走了，则将节点3出栈，即退回到节点2，再将节点4入栈，寻找新的出路。

由此可见，栈不是解决问题的一种方法，而是解决问题的一种方法的模型、结构。

在这里插入图片描述




最大子序和


在这里插入图片描述

看到这个题，很容易想到动态规划：

1.假如全是负数，那就是找最大值即可，因为负数肯定越加越大。

2.如果有正数，则肯定从正数开始计算和，不然前面有负值，和肯定变小了，所以从正数开始。

3.当和小于零时，这个区间就告一段落了，然后从下一个正数重新开始计算(也就是又回到 2 了)，这一步即是动态规划的关键。

我们可以利用队列模拟这种思想。

使用一个队列按顺序存放子序列，用变量sum记录子序列和，用变量result记录当前和的最大值，并且：

1.当队列的首元素小于0时，删除该元素。

2.当子序列之和小于零时，清空队列。

最后得到的result，就是题目的结果。




阻塞队列


线程池主要用来管理线程，提高线程的利用率，防止频繁的创建销毁线程带来的性能消耗。他的主要原理分为以下几步：

  1. 当有任务提交到线程池，线程池首先会根据核心线程数创建线程来处理这些任务
  2. 如果核心线程处理不过来，就放到一个阻塞队列等待
  3. 如果任务在继续来，阻塞队列放不下了，就会创建一些临时线程来处理
  4. 如果临时线程也用完了，就开启拒绝策略。

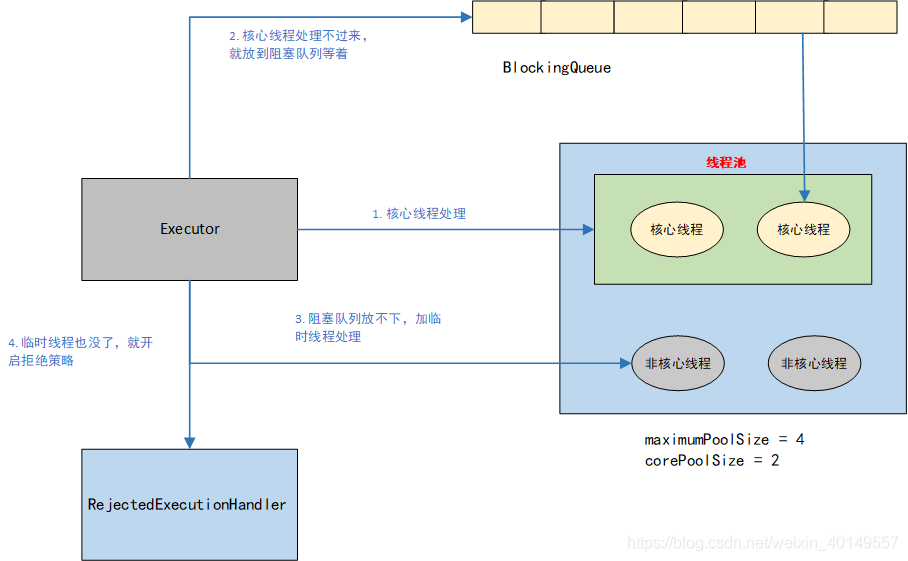
    在这里插入图片描述

以上是线程池管理的大致模型，其中“ 阻塞队列 ”就利用了队列这种数据结构，它里面储存着核心线程还未处理的任务，当核心线程空闲的时候，将新任务添加进去。利用队列的数据结构，让先添加的任务可以先被执行，做到First-In-First-Out。




一点小感悟


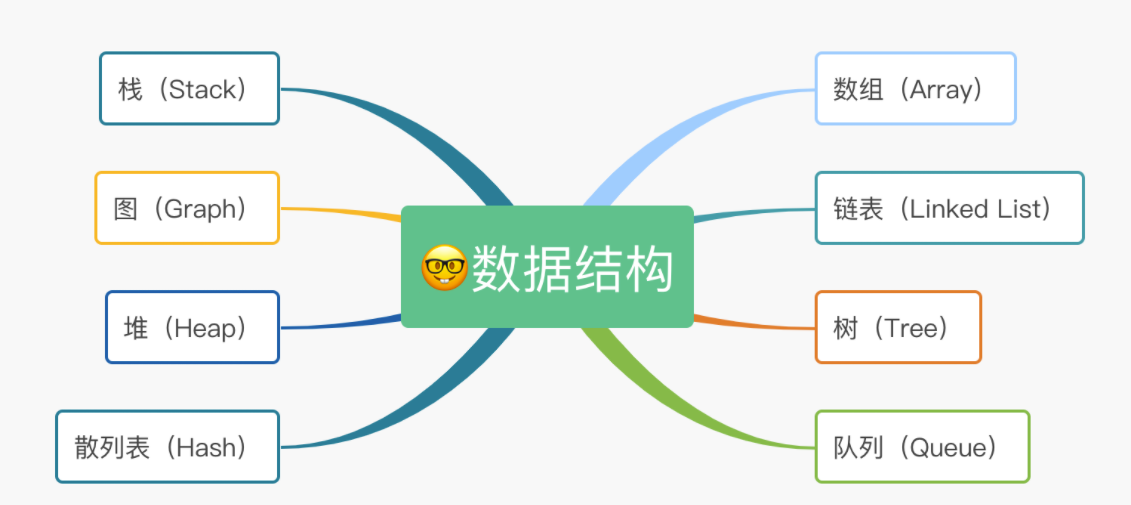
在这里插入图片描述

数据结构分为8类：数组、栈、队列、链表、树、散列表、堆、图。栈和队列各作为一种数据结构，是存放数据的一种方式、一种结构。

为什么会有这些数据结构的存在，是因为用一些特定的方式组织数据，能让问题更好解决。如果我们能够选择合适的数据结构来存储数据，那么在编写程序的过程中，我们对数据的一些操作将会便于实现，实现操作的时间复杂度也会降低，这样程序的效率会提高。

数据结构是计算机存储、组织数据的方式，是指相互之间存在一种或多种特定关系的数据元素的集合。

需要清晰的是，解决问题的是算法，而不是数据结构。通俗的说，算法相当于逻辑，是解决问题的方案。

算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令。

Pascal之父Nicklaus Wirth，仅凭一句话就获得了图灵奖：

.



程序 = 数据结构 + 算法


这个公式是计算机界的质能方程，一个公式就展示出了程序的本质，引领了计算机软件几十年的发展，也告诉了我们，数据结构是程序不可或缺的一部分，学好数据结构是写好程序的前提。


版权声明：本文为LANGJ1原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。